Aufgaben:Aufgabe 1.1Z: Tiefpass 1. und 2. Ordnung

• Zurück zum Buch

Z1.1 Tiefpass 1. und 2. Ordnung

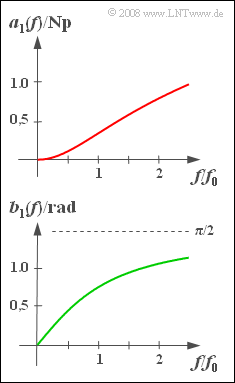
Die einfachste Form eines Tiefpasses – zum Beispiel realisierbar als ein RC–Tiefpass entsprechend der Aufgabe A1.1 – hat den folgenden Frequenzgang: $$H_{\rm 1}(f) = \frac{1}{1+{\rm j}\cdot f/f_0}.$$ Man spricht dann von einem Tiefpass erster Ordnung. Der Dämpfungsverlauf $a_1(f)$ und der Phasenverlauf $b_1(f)$ dieses Filters sind in der Grafik dargestellt.

Entsprechend gilt für einen Tiefpass $n$–ter Ordnung die folgende Definitionsgleichung: $$H_n(f) = H_{\rm 1}(f)^n.$$ In dieser Aufgabe sollen – ausgehend von den Funktionen $a_1(f)$ und $b_1(f)$ eines Tiefpasses erster Ordnung – der Dämpfungs– und Phasenverlauf eines solchen Tiefpasses höherer Ordnung analysiert werden. Allgemein gilt: $$H(f) = {\rm e}^{-a(f) - {\rm j}\cdot b(f)}.$$

Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 1.1. Zwischen dem Np– und dem dB–Wert eines Amplitudenwertes $|H| = 1/x$ besteht folgender Zusammenhang: $$a_{\rm Np} = \ln (x) = \ln (10) \cdot \lg (x) = \frac{\ln (10)}{20} \cdot a_{\rm dB} \approx 0.11513 \cdot a_{\rm dB}.$$ Berücksichtigen Sie weiter, dass für zwei komplexe Größen $z_1$ und $z_2$ folgende Gleichungen gelten: $$|z_1 \cdot z_2| = |z_1| \cdot |z_2|, \hspace{0.5 cm}{\rm arc}\hspace{0.05 cm}(z_1 \cdot z_2) = {\rm arc}\hspace{0.05 cm}(z_1) + {\rm arc}\hspace{0.05 cm}(z_2).$$

Fragebogen

1

Berechnen Sie den Dämpfungsverlauf $a_1(f)$ eines Tiefpasses erster Ordnung in dB. Welche dB–Werte ergeben sich bei $f = f_0$ und $f = 2f_0$?

$a_1(f = f_0)$ = dB

$a_1(f = 2f_0) = dB

2

Input-Box Frage

$\alpha$ =

Musterlösung

Musterlösung

a)

b)

c)

d)

e)

f)

g)