Aufgaben:Aufgabe 1.4: Zum Tiefpass 2. Ordnung: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
Der Zusammenhang zwischen den Systemparametern $R, C$ und $T$ lautet (siehe auch Aufgabe Z1.3): | Der Zusammenhang zwischen den Systemparametern $R, C$ und $T$ lautet (siehe auch Aufgabe Z1.3): | ||
$$T = \frac{1}{\omega_{\rm 0}}= \frac{1}{2\pi f_{\rm 0}} = R C.$$ | $$T = \frac{1}{\omega_{\rm 0}}= \frac{1}{2\pi f_{\rm 0}} = R C.$$ | ||
| − | Für numerische Berechnungen soll im Folgenden $T =$ | + | Für numerische Berechnungen soll im Folgenden $T =$ 1 ms verwendet werden. |
Die untere Schaltung mit Eingang $x(t)$ und Ausgang $y_2(t)$ zeigt einen Tiefpass zweiter Ordnung: | Die untere Schaltung mit Eingang $x(t)$ und Ausgang $y_2(t)$ zeigt einen Tiefpass zweiter Ordnung: | ||
Version vom 12. Juli 2016, 19:21 Uhr
In Aufgabe A1.1 und Aufgabe Z1.1 im Kapitel 1.1 wurden die sog. RC–Tiefpässe im Frequenzbereich beschrieben. Hier soll nun eine Zeitbereichsdarstellung erfolgen.
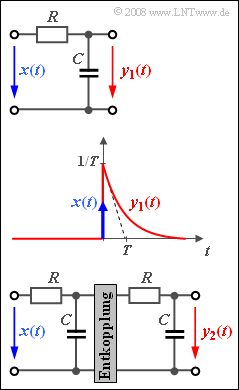
Die oben skizzierte Schaltung mit dem Eingangssignal $x(t)$ und dem Ausgangssignal $y_1(t)$ ist ein Tiefpass erster Ordnung mit dem Frequenzgang $$H_{\rm 1}(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm 0}}.$$
Hierbei gibt $f_0 = 1/(2πRC)$ die 3dB–Grenzfrequenz an. Legt man am Eingang ein diracförmiges Signal $x(t) = δ(t)$ an, so erscheint am Ausgang das Signal $y_1(t)$ gemäß der mittleren Skizze.
Der Zusammenhang zwischen den Systemparametern $R, C$ und $T$ lautet (siehe auch Aufgabe Z1.3): $$T = \frac{1}{\omega_{\rm 0}}= \frac{1}{2\pi f_{\rm 0}} = R C.$$ Für numerische Berechnungen soll im Folgenden $T =$ 1 ms verwendet werden.
Die untere Schaltung mit Eingang $x(t)$ und Ausgang $y_2(t)$ zeigt einen Tiefpass zweiter Ordnung: $$H_{\rm 2}(f) = [H_{\rm 1}(f)]^2 =\frac{1}{(1+{\rm j}\cdot f/f_{\rm 0})^2}.$$ Die zu $H_2(f)$ gehörende Impulsantwort ist $h_2(t)$.
Anzumerken ist, dass der Systemparameter $f_0$ bei einem Tiefpass zweiter oder höherer Ordnung nicht mehr dessen 3 dB–Grenzfrequenz angibt. Weiterhin ist noch zu beachten, dass die beiden RC-Glieder entkoppelt werden müssen, um Widerstandsanpassung zu erreichen. Hierzu eignet sich zum Beispiel ein Operationsverstärker. Dieser Hinweis ist jedoch für die Lösung dieser Aufgabe nicht relevant.
Hinweis: Die Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.2. Zur Lösung dieser Aufgabe können Sie das folgende unbestimmte Integral verwenden: $$\int u \cdot {\rm e}^{a \cdot \hspace{0.03cm} u} \hspace{0.1cm}{\rm d}u = \frac{{\rm e}^{\hspace{0.03cm}a \cdot \hspace{0.03cm} u}}{a^2} \cdot (a \cdot u -1).$$
Fragebogen
Musterlösung