Aufgaben:Aufgabe 1.7: Nahezu kausaler Gaußtiefpass: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Einige systemtheoretische Tiefpassfunktionen}} | {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Einige systemtheoretische Tiefpassfunktionen}} | ||
| − | [[Datei:P_ID863__LZI_A_1_7.png|right|Nahezu kausaler Gaußtiefpass | + | [[Datei:P_ID863__LZI_A_1_7.png|right|Nahezu kausaler Gaußtiefpass]] Messungen haben ergeben, dass ein LZI–System mit guter Näherung durch einen Gaußtiefpass angenähert werden kann, wenn man eine zusätzliche Laufzeit $τ$ berücksichtigt. Somit lautet der Frequenzgang: |
$$H(f) = {\rm e}^{-\pi(f/\Delta f)^2} \cdot {\rm e}^{-{\rm | $$H(f) = {\rm e}^{-\pi(f/\Delta f)^2} \cdot {\rm e}^{-{\rm | ||
j}2\pi f \tau}.$$ | j}2\pi f \tau}.$$ | ||
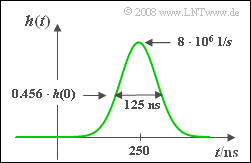
Die beiden Systemparameter $Δt = 1/Δf$ und $τ$ können der in der Grafik dargestellten Impulsantwort $h(t)$ entnommen werden. | Die beiden Systemparameter $Δt = 1/Δf$ und $τ$ können der in der Grafik dargestellten Impulsantwort $h(t)$ entnommen werden. | ||
| − | Es ist offensichtlich, dass dieses Modell nicht exakt der Wirklichkeit entspricht, da die Impulsantwort $h(t)$ auch für $t <$ | + | Es ist offensichtlich, dass dieses Modell nicht exakt der Wirklichkeit entspricht, da die Impulsantwort $h(t)$ auch für $t < 0$ nicht vollkommen verschwindet. In der Teilaufgabe (3) wird deshalb nach dem maximalen relativen Fehler gefragt, der wie folgt definiert ist: |
$$\varepsilon_{\rm max} = \frac{\max_{t \hspace{0.02cm}< | $$\varepsilon_{\rm max} = \frac{\max_{t \hspace{0.02cm}< | ||
\hspace{0.1cm}0}|h(t)|}{h(t = \tau)}.$$ | \hspace{0.1cm}0}|h(t)|}{h(t = \tau)}.$$ | ||
In Worten: Der maximale relative Fehler $ε_{\rm max}$ ist gleich dem Maximalwert der Impulsantwort $h(t)$ bei negativen Zeiten, bezogen auf den maximalen Wert $h(t = τ)$ der Impulsantwort. | In Worten: Der maximale relative Fehler $ε_{\rm max}$ ist gleich dem Maximalwert der Impulsantwort $h(t)$ bei negativen Zeiten, bezogen auf den maximalen Wert $h(t = τ)$ der Impulsantwort. | ||
| − | '' | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört bezieht sich auf die Seite [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen#Gau.C3.9F.E2.80.93Tiefpass|Gaußtiefpass]] . | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
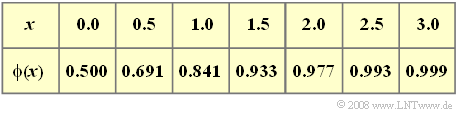
| + | *Zur Berechnung von Sprung– und Rechteckantwort können Sie das Gaußsche Fehlerintegral verwenden: | ||
$${\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot | $${\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot | ||
\int\limits_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$ | \int\limits_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$ | ||
| − | [[Datei:P_ID864__LZI_A_1_7b.png | Werte der Gaußschen Fehlerfunktion | + | [[Datei:P_ID864__LZI_A_1_7b.png | Werte der Gaußschen Fehlerfunktion]] |
| Zeile 25: | Zeile 28: | ||
{Wie groß sind die äquivalente Bandbreite und die Laufzeit? | {Wie groß sind die äquivalente Bandbreite und die Laufzeit? | ||
|type="{}"} | |type="{}"} | ||
| − | $\Delta f =$ { 8 } MHz | + | $\Delta f \ =$ { 8 3% } $\ \rm MHz$ |
| − | $\tau =$ { 250 } ns | + | $\tau =$ { 250 3% } $\ \rm ns$ |
| − | {Es gelte $x(t) = 1 {\rm V} · \cos(2π · 6 {\rm MHz }· t)$. Wie lautet das Ausgangssignal $y(t)$? Welcher Signalwert ergibt sich zur Zeit $t =$ | + | {Es gelte $x(t) = 1 {\rm V} · \cos(2π · 6 {\rm MHz }· t)$. Wie lautet das Ausgangssignal $y(t)$? Welcher Signalwert ergibt sich zur Zeit $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $y(t = 0) =$ { -0.175--0.165 } V | + | $y(t = 0) \ =$ { -0.175--0.165 } $\ \rm V$ |
| − | {Eigentlich sollte bei Kausalität $h(t < 0) =$ | + | {Eigentlich sollte bei Kausalität $h(t < 0) = 0$ gelten. Wie groß ist der maximale relative Fehler des betrachteten Modells? Definition siehe Angabenseite. |
|type="{}"} | |type="{}"} | ||
| − | $\epsilon_{\rm max} =$ { 3.49 5% } $\ | + | $\epsilon_{\rm max} \ =$ { 3.49 5% } $\ \cdot 10^{-6}$ |
| − | {Berechnen Sie die (dimensionslose) Sprungantwort $σ(t)$. Welche Werte ergeben sich zu den Zeiten $t = | + | {Berechnen Sie die (dimensionslose) Sprungantwort $σ(t)$. Welche Werte ergeben sich zu den Zeiten $t = 250 \ \rm ns$ und $t = 300 \ \rm ns$ ? |
|type="{}"} | |type="{}"} | ||
| − | $σ(t = 250 \rm ns) =$ { 0.5 5% } | + | $σ(t = 250\ \rm ns) =$ { 0.5 5% } |
| − | $σ(t = 300 \rm ns) =$ { 0.841 5% } | + | $σ(t = 300\ \rm ns) =$ { 0.841 5% } |
</quiz> | </quiz> | ||
Version vom 30. Januar 2017, 10:47 Uhr
Messungen haben ergeben, dass ein LZI–System mit guter Näherung durch einen Gaußtiefpass angenähert werden kann, wenn man eine zusätzliche Laufzeit $τ$ berücksichtigt. Somit lautet der Frequenzgang:
$$H(f) = {\rm e}^{-\pi(f/\Delta f)^2} \cdot {\rm e}^{-{\rm j}2\pi f \tau}.$$ Die beiden Systemparameter $Δt = 1/Δf$ und $τ$ können der in der Grafik dargestellten Impulsantwort $h(t)$ entnommen werden.
Es ist offensichtlich, dass dieses Modell nicht exakt der Wirklichkeit entspricht, da die Impulsantwort $h(t)$ auch für $t < 0$ nicht vollkommen verschwindet. In der Teilaufgabe (3) wird deshalb nach dem maximalen relativen Fehler gefragt, der wie folgt definiert ist: $$\varepsilon_{\rm max} = \frac{\max_{t \hspace{0.02cm}< \hspace{0.1cm}0}|h(t)|}{h(t = \tau)}.$$ In Worten: Der maximale relative Fehler $ε_{\rm max}$ ist gleich dem Maximalwert der Impulsantwort $h(t)$ bei negativen Zeiten, bezogen auf den maximalen Wert $h(t = τ)$ der Impulsantwort.
Hinweise:
- Die Aufgabe gehört bezieht sich auf die Seite Gaußtiefpass .
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Zur Berechnung von Sprung– und Rechteckantwort können Sie das Gaußsche Fehlerintegral verwenden:
$${\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int\limits_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$
Fragebogen
Musterlösung
- a) Die äquivalente Bandbreite $Δf$ ist gleich $h(t = τ) \ \rm \underline{= \ 8 \ MHz}$. Dies ist gleichzeitig der Kehrwert der äquivalenten Impulsdauer $Δt =$ 125 ns. Auch die Phasenlaufzeit $τ \ \rm \underline{= \ 250 \ ns}$ kann direkt aus der Grafik abgelesen werden.
- b) Ohne Berücksichtigung der Laufzeit ergäbe sich ein Cosinussignal mit der Amplitude
$$A_y = 1\,{\rm V} \cdot {\rm e}^{-\pi({ {6\,\rm MHz} }/{ {8\,\rm MHz} })^2}= 0.171\,{\rm V}.$$
- Die Laufzeit bewirkt eine Phasenverschiebung um $3π$:
$$\begin{align*} y(t) & = A_y \cdot {\rm cos}(2\pi f_0 ( t - \tau) ) = A_y \cdot {\rm cos}(2\pi f_0 t - 2\pi \cdot {6\,\rm MHz}\cdot {250\,\rm ns} ) \\ & = A_y \cdot {\rm cos}(2\pi f_0 t - 3\pi ) = -A_y \cdot {\rm cos}(2\pi f_0 t ).\end{align*}$$
- Der gesuchte Wert ist somit $y(t = 0) \ \rm \underline{= \ –0.171 \ V}$.
- c) Die Impulsantwort lautet:
$$h(t) = h_{\rm GTP}(t - \tau) =\Delta f \cdot {\rm e}^{-\pi(\frac{t - \tau}{\Delta t})^2} .$$
- Da $h(t)$ im Bereich $t <$ 0 stetig zunimmt, tritt der Maximalwert (bei negativen Zeiten) etwa bei $t =$ 0 auf:
$$h(t = 0) = \Delta f \cdot {\rm e}^{-\pi(\frac{ \tau}{\Delta t})^2}= \Delta f \cdot {\rm e}^{-4\pi} .$$
- Mit $h(t = τ) = Δf$ erhält man so:
$$\varepsilon_{\rm max}= {\rm e}^{-4\pi}\hspace{0.15cm}\underline{ \approx 3.49 \cdot 10^{-6}} .$$
- d) Wir lassen vorerst die Phasenlaufzeit $τ$ des zweiten Systems außer Betracht und berechnen die Sprungantwort des Gaußtiefpasses:
$$\sigma_{\rm GTP}(t) = \frac{1}{\Delta t} \cdot \int\limits_{ -\infty }^{ t } {{\rm e}^{-\pi \left({t'}/{\Delta t}\right)^2}} \hspace{0.1cm}{\rm d}t'.$$
- Nach der Substitution $t ' → u$ sowie mit dem Gaußschen Fehlerintegral $ϕ(x)$ erhält man
$$\sigma_{\rm GTP}(t) = \frac{1}{\sqrt{2 \pi } } \cdot \int\limits_{ -\infty }^{ \sqrt{2\pi}\cdot\hspace{0.05cm} t / \Delta t } { {\rm e}^{-u^2/2} } \hspace{0.1cm}{\rm d}u = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t}{\Delta t }),$$ $${\rm nach\hspace{0.15cm} Substitution\hspace{-0.15cm}:}\hspace{0.3cm}u = \frac{\sqrt{2\pi}}{\Delta t} \cdot t' , \hspace{0.3cm}{\rm wobei} \hspace{0.15cm}\hspace{0.2cm} {\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int\limits_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$
- Unter Berücksichtigung der Laufzeit $τ$ erhält man für die gesamte Sprungantwort:
$$\sigma(t) = \sigma_{\rm GTP}(t - \tau) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t - \tau}{\Delta t }).$$
- Der Wert bei $t = τ =$ 250 ns ergibt sich zu $\ \rm \underline{ϕ(0) \ = \ 0.500}$. Entsprechend erhält man für $t =$ 300 ns:
$$\sigma(t = {300\,\rm ns}) = \sigma_{\rm GTP}(t = {50\,\rm ns}) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{ {50\,\rm ns} }{ {125\,\rm ns} })\approx {\rm \phi}(1)\hspace{0.15cm}\underline{ = 0.841}.$$