Aufgaben:Aufgabe 3.2Z: Zusammenhang zwischen WDF und VTF

• Zurück zum Buch

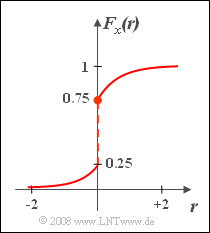
Gegeben ist die Zufallsgröße $x$ mit der Verteilungsfunktion

$$ F_x(r)=\left\{\begin{array}{*{4}{c}} 0.25\cdot {\rm e}^{2\it r} &\rm f\ddot{u}r\hspace{0.1cm}\it r<\rm 0, \\ 1-0.25\cdot {\rm e}^{-2\it r} & \rm f\ddot{u}r\hspace{0.1cm}\it r\ge\rm 0. \\\end{array}\right.$$

Diese Funktion ist rechts dargestellt. Es ist zu erkennen, dass an der Sprungstelle $r = 0$ der rechtsseitige Grenzwert gültig ist.

Hinweis: Diese Aufgabe bezieht sich auf den gesamten Inhalt von Kapitel 3.1 und Kapitel 3.2.

Eine Zusammenfassung der hier behandelten Thematik bietet das folgende Lernvideo:

Fragebogen

1

Welche Eigenschaften einer Verteilungsfunktion (VTF) gelten allgemein, also nicht nur bei diesem konkreten Beispiel?

	Die VTF steigt von 0 auf 1 zumindest schwach monoton an.
	Die Fx(r)-Werte 0 und 1 sind für endliche r-Werte möglich.
	Ein horizontaler Abschnitt weist darauf hin, dass in diesem Bereich die Zufallsgröße keine Anteile besitzt.
	Vertikale Abschnitte sind möglich.

2

Wie groß ist die Wahrscheinlichkeit, dass x positiv ist?

$Pr(x > 0)$ =

3

Wie groß ist die Wahrscheinlichkeit, dass |x| größer ist als 0.5?

$Pr (|x| > 0.5)$ =

4

Geben Sie die zugehörige WDF f_x(x) allgemein und den Wert für x = 1 an.

$f_x(x\ =\ 1)$ =

5

Wie groß ist die Wahrscheinlichkeiten, dass x genau gleich 1 ist?

$Pr(x = 1)$=

6

Wie groß ist die Wahrscheinlichkeiten, dass x genau gleich 0 ist?

$Pr(x = 0)$ =

Musterlösung

Musterlösung

1.  Die Aussagen 1, 3 und 4 sind immer richtig. Ist jedoch x auf den Bereich von x_min bis x_max begrenzt, so ist F_x(r) = 0 für r < x_min und F_x(r) = 1 für r > x_max. In diesem Sonderfall wäre auch die Aussage 2 zutreffend.

Ein horizontaler Abschnitt in der VTF weist darauf hin, dass die Zufallsgröße in diesem Bereich keine Werte besitzt. Dagegen weist ein vertikaler Abschnitt in der VTF auf eine Diracfunktion in der WDF (an gleicher Stelle x₀) hin. Dies bedeutet, dass die Zufallsgröße den Wert x₀ sehr häufig annimmt, nämlich mit endlicher Wahrscheinlichkeit. Alle anderen Werte treten exakt mit der Wahrscheinlichkeit 0 auf.

2.  Die gesuchte Wahrscheinlichkeit kann man aus der Differenz der VTF-Werte an den Grenzen berechnen:

$$\rm Pr(\it x>\rm 0)=\it F_x(\infty)-\it F_x(\rm 0) \hspace{0.15cm}\underline{=\rm 0.25}.$$

3.  Für die Wahrscheinlichkeit, dass x größer als 0.5 ist, gilt:

$$\rm Pr(\it x>\rm 0.5)=1- \it F_x(\rm 0.5)=\rm 0.25\cdot e^{-1} \hspace{0.15cm}{\approx0.092}. $$

Aus Symmetriegründen ist Pr(x < –0.5) genauso groß. Daraus folgt:

$$\rm Pr( |\it x| >\rm 0.5) \hspace{0.15cm}\underline{= \rm 0.184}.$$

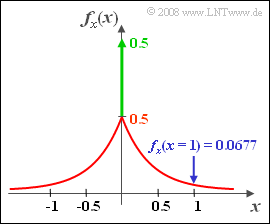
4.  Die WDF erhält man aus der zugehörigen VTF durch Differenzieren der zwei Bereiche. Es ergibt sich eine zweiseitige Exponentialfunktion sowie eine Diracfunktion bei x = 0:

$$f_x(x)=\rm 0.5\cdot \rm e^{-2\cdot |\it x|} + \rm 0.5\cdot\delta(\it x).$$

Für x = 1 ergibt sich der Zahlenwert 0.0677.

Hinweis. Für die zweiseitige Exponentialverteilung ist der Begriff „Laplaceverteilung” gebräuchlich.

5.  Im Bereich um 1 beschreibt x eine kontinuierliche Zufallsgröße. Die Wahrscheinlichkeit, dass x exakt den Wert 1 aufweist, ist deshalb 0.

6.  In 50% der Zeit wird x = 0 gelten: Pr(x = 0) = 0.5. Hinweis: Die WDF eines Sprachsignals wird häufig durch eine zweiseitige Exponentialfunktion beschrieben (siehe Lernvideo zu Kap. 3.1). Die Diracfunktion bei x = 0 berücksichtigt vor allem Sprachpausen – hier in 50% aller Zeiten.