Aufgaben:Aufgabe 3.12: Cauchyverteilung: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Weitere Verteilungen }} right| :Die Wahrscheinlichkeitsdichtefunktion s…“) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID207__Sto_A_3_12.png|right|]] | + | [[Datei:P_ID207__Sto_A_3_12.png|right|Cauchyverteilung]] |
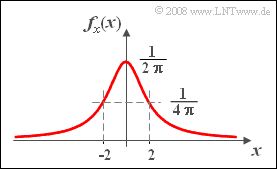
| − | + | Die Wahrscheinlichkeitsdichtefunktion der Cauchyverteilung ist wie folgt gegeben: | |
| − | + | $$f_x(x)=\frac{\rm 1}{\rm 2 \pi}\cdot \frac{\rm 1}{\rm 1+ (\it x/\rm 2)^{\rm 2}}.$$ | |
| − | + | Aus der Grafik ist bereits der extrem langsame Abfall des WDF–Verlaufs zu erkennen. | |
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Weitere_Verteilungen|Weitere Verteilungen]]. | ||
| + | *Insbesondere wird auf die Seite [[Stochastische_Signaltheorie/Weitere_Verteilungen#Cauchyverteilung|TCauchyverteilung]] Bezug genommen . | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| − | |||
| Zeile 15: | Zeile 20: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lautet die Verteilungsfunktion | + | {Wie lautet die Verteilungsfunktion $F_x(r)$? Mit welcher Wahrscheinlichkeit ist $x$ betragsmäßig kleiner als $2$? |
|type="{}"} | |type="{}"} | ||
| − | $Pr (|x| < 2)$ | + | ${\rm Pr} (|x| < 2) \ = $ { 0.5 3% } |
| − | {Mit welcher Wahrscheinlichkeit ist | + | {Mit welcher Wahrscheinlichkeit ist$x$ betragsmäßig größer als $4$? |
|type="{}"} | |type="{}"} | ||
| − | $Pr (|x| > 4)$ | + | ${\rm Pr} (|x| > 4) \ = $ { 0.296 3% } |
| − | {Welche der | + | {Welche der folgenden Aussagen treffen für die Cauchyverteilung zu? |
|type="[]"} | |type="[]"} | ||
+ Die Cauchyverteilung besitzt eine unendlich große Varianz. | + Die Cauchyverteilung besitzt eine unendlich große Varianz. | ||
Version vom 15. März 2017, 17:17 Uhr
Die Wahrscheinlichkeitsdichtefunktion der Cauchyverteilung ist wie folgt gegeben: $$f_x(x)=\frac{\rm 1}{\rm 2 \pi}\cdot \frac{\rm 1}{\rm 1+ (\it x/\rm 2)^{\rm 2}}.$$
Aus der Grafik ist bereits der extrem langsame Abfall des WDF–Verlaufs zu erkennen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Verteilungen.
- Insbesondere wird auf die Seite TCauchyverteilung Bezug genommen .
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- 1. Vergleicht man die vorgegebene WDF mit der allgemeinen Gleichung im Kapitel 3.7, so erkennt man, dass der Parameter λ = 2 ist. Daraus folgt (nach Integration über die WDF):
- $$F_x ( r ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(\it r/\rm 2).$$
- Insbesondere sind
- $$F_x ( r = 2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(1)=\frac{1}{2} + \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.75,$$
- $$F_x ( r = -2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(-1)=\frac{1}{2} - \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.25.$$
- Daraus ergibt sich die gesuchte Wahrscheinlichkeit als die Differenz zu 50%.
- 2. Nach dem Ergebnis aus (a) ist Fx(4.0) = 0.5 + 1/π = 0.852. Damit gilt für die „komplementäre” Wahrscheinlichkeit Pr(x > 4) = 0.148. Die gesuchte Wahrscheinlichkeit ist doppelt so groß:
- $${\rm Pr} (|x| >4) \hspace{0.15cm}\underline{ = 0.296}.$$
- 3. Alle Lösungsvorschläge treffen zu. Für die Varianz der Cauchyverteilung gilt nämlich:
- $$\sigma_x^{\rm 2}=\frac{1}{2\pi}\int_{-\infty}^{+\infty} \hspace{-0.15cm} \frac{\it x^{\rm 2}}{\rm 1+(\it x/\rm 2)^{\rm 2}} \,\,{\rm d}x.$$
- Für große x liefert der Integrand den konstanten Wert 4. Deshalb divergiert das Integral. Mit <nobr>σx → ∞</nobr> liefert aber auch die Tschebyscheffsche Ungleichung keine auswertbare Schranke.
„Natürliche“ Zufallsgrößen (physikalisch interpretierbar) können nie cauchyverteilt sein, da sie sonst eine unendlich große Leistung besitzen müssten. Dagegen unterliegt eine „künstliche“ (oder mathematische) Zufallsgröße - wie z. B. der Quotient zweier mittelwertfreier Gaußgrößen - nicht dieser Beschränkung.