Aufgaben:Aufgabe 2.7: Huffman-Anwendung für binäre Zweiertupel

• Zurück zum Buch

Die Anwendung des Huffman–Algorithmus in seiner ursprünglichen Form setzt einen Symbolumfang M > 2 voraus und ist deshalb zur Datenkomprimierung von Binärquellen unbrauchbar.

Fasst man aber mehrere aufeinanderfolgende Binärzeichen der Nachrichtenquelle zu einem neuen Symbol zusammen, so kann man auf die neue Symbolmenge die Huffman–Datenkomprimierung sinnvoll anwenden.

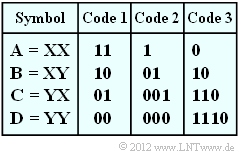
Wir gehen in dieser Aufgabe von der Symbolmenge {X, Y}  ⇒  M = 2 aus und bilden gemäß der obigen Tabelle Zweiertupel mit dem Symbolvorrat {A, B, C, D}  ⇒  M ′ = M ² = 4. Aus der binären Quellensymbolfolge XYXXYXXXYY wird somit die quaternäre Folge BACAD.

Desweiteren sind in obiger Tabelle drei Codes angegeben, von denen manche durch den Huffman–Algorithmus entstanden sind. Die binären Ausgangsfolgen ergeben sich dann für unser Beispiel wie folgt:

• Code 1:   1011011100,

• Code 2:   0110011000,

• Code 3:   10011001110.

Nochmals zum Verständnis: Aus der ursprünglichen Symbolmenge {X, Y} erhält man durch die Bildung von Zweiertupeln eine Quaternärmenge mit dem Symbolvorrat {A, B, C, D}. Die Folgenlänge N wird dadurch halbiert. Durch Huffman–Codierung ergibt sich wieder eine Binärfolge, deren Symbolmenge zur besseren Unterscheidung mit {0, 1} bezeichnet wird. Die Anwendung der Huffman–Codierung macht genau dann Sinn, wenn die Länge der Ausgangsfolge (im statistischen Mittel) kleiner ist als N.

Mit dieser Aufgabe soll geklärt werden, welche der vorgegebenen Binärcodes bei welchen Randbedingungen sinnvoll sind. Die binäre Nachrichtenquelle {X, Y} sei gedächtnislos und wird allein durch die Symbolwahrscheinlichkeiten p_X beschrieben. Die zweite Wahrscheinlichkeit ist dann stets p_Y = 1 – p_X.

Hinweis: Die Aufgabe bezieht sich auf die letzte Theorieseite von Kapitel 2.3. Die Idee zu dieser Aufgabe entstand bei einem Vortrag von Prof. Robert Fischer von der Universität Ulm zum Thema „Der goldene Schnitt in der Nachrichtentechnik”.

Für die mittlere Codewortlänge pro Zweiertupel gilt:

$$L_{\rm M}' = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B} + p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm}.$$

Bezogen auf ein Quellensymbol ergibt sich L_M = L′_M/2.

Fragebogen

1

Geben Sie die Codewortlängen bei redundanzfreier Binärquelle an.

Code 1: $L_M$ = bit/Quellensymbol

Code 2: $L_M$ = bit/Quellensymbol

Code 3: $L_M$ = bit/Quellensymbol

2

Ermitteln Sie den Huffman–Code hinsichtlich Zweiertupel für p_X = 0.6.

	Es ergibt sich Code 1.
	Es ergibt sich Code 2.
	Es ergibt sich Code 3.

3

Wie groß ist die zugehörige mittlere Codewortlänge?

$p_X = 0.6:\ L_M$ = bit/Quellensymbol

4

Ermitteln Sie den Huffman–Code hinsichtlich Zweiertupel für p_X = 0.8.

	Es ergibt sich Code 1.
	Es ergibt sich Code 2.
	Es ergibt sich Code 3.

5

Wie groß ist die zugehörige mittlere Codewortlänge?

$p_X = 0.8:\ L_M$ = bit/Quellensymbol

6

In welchem Bereich darf die Wahrscheinlichkeit p_X für das Symbol X liegen, damit sich Code 1 als Huffman–Code ergibt?

$p_\text{X,max}$ =

$p_\text{X,min}$ =

Musterlösung

Musterlösung

1  Bei redundanzfreier Binärquelle (p_X = p_Y = 1/2) erhält man p_A = p_B = p_C = p_D = 1/4 und mit der angegebenen Gleichung:

$$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} \big [ \hspace{0.05cm}p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B} + p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm} \big ] / 2 = \\ \hspace{0.2cm} = \hspace{0.2cm} \big [ \hspace{0.05cm} L_{\rm A} + L_{\rm B} + L_{\rm C} + L_{\rm D}\hspace{0.05cm} \big ] / 8 \hspace{0.05cm}.$$

Berücksichtigt man die angegebenen Zuordnungen, so erhält man für

• Code 1:    L_M = 1.000 bit/Quellensymbol,

• Code 2:    L_M = 1.125 bit/Quellensymbol,

• Code 3:    L_M = 1.250 bit/Quellensymbol.

Im Verlauf der Aufgabe wird sich zeigen, dass die beiden ersten Codes durchaus als Ergebnis des Huffman–Algorithmus möglich sind (natürlich nur bei geeigneten Symbolwahrscheinlichkeiten). Code 3 ist zwar ebenfalls präfixfrei, aber hinsichtlich der mittleren Codewortlänge nie optimal.

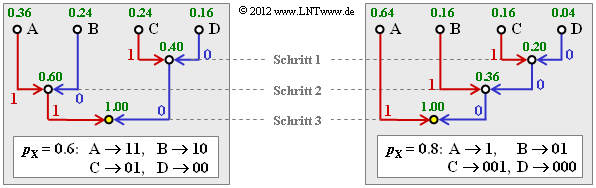
2.  Die Wahrscheinlichkeiten der möglichen Zweiertupel lauten:

$$p_{\rm A} = 0.6^2 = 0.36 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B}= 0.6 \cdot 0.4 = 0.24 = p_{\rm C} \hspace{0.05cm},\hspace{0.2cm} p_{\rm D}= 0.4^2 = 0.16 \hspace{0.05cm}.$$

Damit ergibt sich das linke Baumdiagramm (siehe Grafik) und der folgende Huffman–Code:

A → 11,   B → 10,   C → 01,   D → 00.

Es handelt sich um den Code 1   ⇒   Lösungsvorschlag 1.

3.  Jedes Zweiertupel wird durch zwei Bit dargestellt. Damit ist L_M = 1 bit/Quellensymbol.

4.  Hier lauten die Wahrscheinlichkeiten der einzelnen Zweiertupel:

$$p_{\rm A} = 0.8^2 = 0.64 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B}= 0.8 \cdot 0.2 = 0.16 = p_{\rm C} \hspace{0.05cm},\hspace{0.2cm} p_{\rm D}= 0.2^2 = 0.04 \hspace{0.05cm}. $$

Entsprechend dem rechten Baumdiagramm ergibt sich nun Code 2   ⇒   Lösungsvorschlag 2:

A → 1,   B → 01,   C → 011,   D → 010.

5.  Hier gilt für die mittlere Zweiertupellänge bzw. die mittlere Codewortlänge:

$$L_{\rm M}' = 0.64 \cdot 1 + 0.16 \cdot 2 + (0.16 + 0.04) \cdot 3 = 1.56\,{\rm bit/Zweiertupel}$$

$$\Rightarrow\hspace{0.3cm}L_{\rm M} = \frac{L_{\rm M}'}{2}\hspace{0.15cm}\underline{ = 0.78\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$

6.  Beispielsweise ist für p_X = 0.8 entsprechend der Teilaufgabe (4) der Code 2 optimal und die mittlere Codewortlänge beträgt L_M = 0.78 bit/Quellensymbol. Für p_X = 0.6 ist dagegen Code 1 optimal und die mittlere Codewortlänge ist L_M = 1 bit/Quellensymbol (dieses Ergebnis ist unabhängig von p_X).

Der gesuchte Maximalwert p_X, max wird zwischen 0.6 und 0.8 liegen. Die Bestimmungsgleichung ist dabei, dass für den Grenzfall p_X = p_X, max beide Codes genau die gleiche mittlere Codewortlänge L_M = 1 bit/Quellensymbol besitzen, bzw. L′_M = 2 bit/Zweiertupel.

Mit der Abkürzung p = p_{X, max} lautet die Gleichung:

$$L_{\rm M}'\hspace{0.15cm}{\rm (Code \hspace{0.15cm}2)} = p^2 \cdot 1 + p \cdot (1-p) \cdot 2 + p \cdot (1-p) \cdot 3 + (1-p)^2 \cdot 3 \stackrel{!}{=} 2 \hspace{0.05cm}.$$

Dies führt zum zahlenmäßigen Ergebnis:

$$p^2 + p - 1 \stackrel{!}{=} 0 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} p_{\rm X,\hspace{0.05cm}max} = p = \frac{\sqrt{5}-1}{2} \hspace{0.15cm}\underline{ \approx 0.618} \hspace{0.05cm}.$$

Da sich die grundsätzliche Huffman–Struktur durch Vertauschen von X und Y nicht ändert, gilt für die untere Grenze:

$$p_{\rm X,\hspace{0.05cm}min} = 1 - p_{\rm X,\hspace{0.05cm}max}\hspace{0.15cm}\underline{ \approx 0.382} \hspace{0.05cm}.$$

Die Darstellung der Zweiertupel durch unterschiedlich lange Bitfolgen (Code 2) macht also nur dann Sinn, wenn sich die Symbolwahrscheinlichkeiten von X und Y signifikant unterscheiden. Liegen diese dagegen zwischen 0.382 und 0.618, so ist Code 1 anzuwenden.

Die Aufteilung einer Strecke der Länge 1 in zwei Abschnitte der Länge 0.618... und 0.382... bezeichnet man als Goldenen Schnitt, auf den man in den verschiedensten Fachgebieten immer wieder stößt.