Aufgaben:Aufgabe 2.6Z: Betrag und Phase: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Signaldarstellung/Fourierreihe }} right| Es soll der Zusammenhang zwischen :* den reellen Fourierko…“) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID348__Sig_Z_2_6.png|right|]] | + | [[Datei:P_ID348__Sig_Z_2_6.png|right|Zu analysierendes Signal]] |
Es soll der Zusammenhang zwischen | Es soll der Zusammenhang zwischen | ||
| Zeile 10: | Zeile 10: | ||
:* den komplexen Koeffizienten $D_n$, sowie | :* den komplexen Koeffizienten $D_n$, sowie | ||
| − | :* den Betrags– | + | :* den Betrags– bzw. Phasenkoeffizienten ($C_n$, $\varphi_n$) |
aufgezeigt werden. | aufgezeigt werden. | ||
| Zeile 19: | Zeile 19: | ||
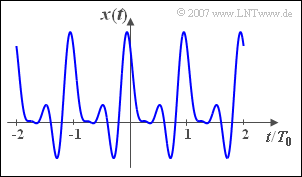
Dieses Signal ist in obiger Grafik im Bereich von $–2T_0$ bis $+2T_0$ dargestellt. | Dieses Signal ist in obiger Grafik im Bereich von $–2T_0$ bis $+2T_0$ dargestellt. | ||
| − | + | ''Hinweise:'' | |
| + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fourierreihe|Fourierreihe]]. | ||
| + | *Eine kompakte Zusammenfassung der Thematik finden Sie in den folgenden Lernvideos [[Zur Berechnung der Fourierkoeffizienten (Dauer 3:50)]] und [[Eigenschaften und Genauigkeit der Fourierreihe]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
| Zeile 26: | Zeile 30: | ||
{Welche Werte besitzen die Koeffizienten $A_0$, $D_0$, $C_0$ und $\varphi_0$? | {Welche Werte besitzen die Koeffizienten $A_0$, $D_0$, $C_0$ und $\varphi_0$? | ||
|type="{}"} | |type="{}"} | ||
| − | $C_0$ = { 1 3% } $\text{V}$ | + | $C_0$ = { 1 3% } $\text{V}$ |
| − | $\varphi_0$ = { 0 | + | $\varphi_0$ = { 0. } $\text{Grad}$ |
{Welche der Cosinus– und Sinuskoeffizienten sind ungleich Null? | {Welche der Cosinus– und Sinuskoeffizienten sind ungleich Null? | ||
|type="[]"} | |type="[]"} | ||
| − | + $A_1$ | + | + $A_1$, |
| − | - $B_1$ | + | - $B_1$, |
| − | + $A_2$ | + | + $A_2$, |
| − | + $B_2$ | + | + $B_2$, |
| − | - $A_3$ | + | - $A_3$, |
| − | + $B_3$ | + | + $B_3$. |
{Welche Werte besitzen die Koeffizienten $\varphi_1$, $C_1$ und $D_1$? | {Welche Werte besitzen die Koeffizienten $\varphi_1$, $C_1$ und $D_1$? | ||
|type="{}"} | |type="{}"} | ||
| − | $\varphi_1$ = { 0 3% } $\text{Grad}$ | + | $\varphi_1$ = { 0 3% } $$\text{Grad}$ |
| − | $C_1$ = { 2 3% } $\text{V}$ | + | $C_1$ = { 2 3% } $$\text{V}$ |
| − | $\text{Re}[D_1]$ = { 1 3% } $\text{V}$ | + | $\text{Re}[D_1]$ = { 1 3% } $$\text{V}$ |
| − | $\text{Im}[D_1]$ = { | + | $\text{Im}[D_1]$ = { 0. } $$\text{V}$ |
{Welche Werte besitzen die Koeffizienten $\varphi_2$, $C_2$ und $D_2$? | {Welche Werte besitzen die Koeffizienten $\varphi_2$, $C_2$ und $D_2$? | ||
|type="{}"} | |type="{}"} | ||
| − | $\varphi_2$ = | + | $\varphi_2$ = { -26.6--26.5 } $\text{Grad}$ |
| − | $C_2$ = { 2.236 3% } $\text{V}$ | + | $C_2$ = { 2.236 3% } $\text{V}$ |
| − | $\text{Re}[D_2]$ = { 1 3% } $\text{V}$ | + | $\text{Re}[D_2]$ = { 1 3% } $\text{V}$ |
| − | $\text{Im}[D_2]$ = { 0.5 3% } $\text{V}$ | + | $\text{Im}[D_2]$ = { 0.5 3% } $\text{V}$ |
| Zeile 59: | Zeile 63: | ||
{Welche Werte besitzen die Koeffizienten $\varphi_3$ und $C_3$? | {Welche Werte besitzen die Koeffizienten $\varphi_3$ und $C_3$? | ||
|type="{}"} | |type="{}"} | ||
| − | $\varphi_3$ = | + | $\varphi_3$ = { -91--89 } $\text{Grad}$ |
| − | $C_3$ = { 1 3% } $\text{V}$ | + | $C_3$ = { 1 3% } $\text{V}$ |
{Wie groß ist der komplexe Fourierkoeffizient $D_\text{–3}$? | {Wie groß ist der komplexe Fourierkoeffizient $D_\text{–3}$? | ||
|type="{}"} | |type="{}"} | ||
| − | $\text{Re}[D_3]$ = { 0 | + | $\text{Re}[D_3]$ = { 0. } $\text{V}$ |
| − | $\text{Im}[D_3]$ = $-$ { 0. | + | $\text{Im}[D_3]$ = $-$ { -0.51--0.49 } $\text{V}$ |
Version vom 16. Januar 2017, 14:01 Uhr
Es soll der Zusammenhang zwischen
- den reellen Fourierkoeffizienten $A_n$ und $B_n$,
- den komplexen Koeffizienten $D_n$, sowie
- den Betrags– bzw. Phasenkoeffizienten ($C_n$, $\varphi_n$)
aufgezeigt werden.
Dazu betrachten wir das periodische Signal
- $$x(t)=1{\rm V+2V}\cdot\cos(\omega_0 t) +{\rm 2V}\cdot\cos(2\omega_0 t)- \ {\rm 1V}\cdot\sin(2\omega_0 t)-{\rm 1V}\cdot\sin(3\omega_0 t).$$
Dieses Signal ist in obiger Grafik im Bereich von $–2T_0$ bis $+2T_0$ dargestellt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Fourierreihe.
- Eine kompakte Zusammenfassung der Thematik finden Sie in den folgenden Lernvideos Zur Berechnung der Fourierkoeffizienten (Dauer 3:50) und Eigenschaften und Genauigkeit der Fourierreihe.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
1. Der Gleichsignalkoeffizient beträgt $A_0 = 1 V$. Gleichzeitig gilt $C_0 = D0 = A0 \rightarrow C_0 \underline{= 1}, \varphi_0 \underline{= 0}$.
2. Es gibt keine Anteile mit $sin(\omega_0t)$ und $cos(3\omega_0t)$. Daraus folgt direkt $B_1 = A_3 = 0$. Alle anderen hier aufgeführten Koeffizienten sind ungleich 0. ⇒ Richtig sind also die Antworten 1, 3, 4 und 6.
3. Allgemein gilt:
- $$\varphi_n=\arctan\left(\frac{B_n}{A_n}\right),\hspace{0.5cm}C_n=\sqrt{A_n^2+B_n^2},\hspace{0.5cm}D_n=\frac{1}{2}(A_n-{\rm j}B_n).$$
Wegen $B_1 = 0$ erhält man $\varphi_1 = 0, C_1 = A_1 = 2 V$ und $D_1 = A_1/2 = 1 V$.
4. Mit $A_2 = 2 V$ und $B_2 = –1 V$ erhält man:
- $$\varphi_2=\arctan(-0.5)\hspace{0.15cm}\underline{=-26.56^{\rm o}},\hspace{0.5cm}C_2=\sqrt{A_2^2+B_2^2}\hspace{0.15cm}\underline{=2.236 \; \rm V},$$
- $$D_2=\frac{1}{2}(A_2-{\rm j}\cdot B_2)=1\;\rm V+{\rm j}\cdot 0.5 \rm V \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Re}[D_2]\hspace{0.15cm}\underline{ = 1 V}, \hspace{0.2cm}{\rm Im}[D_2]\hspace{0.15cm}\underline{ = 0.5 V} .$$
5. Es ist $\varphi_3 = –90°$ und $C_3 = |B_3| = 1 V$.
6. Es gilt $D_3 = –j · B_3/2 = j · 0.5 V$ und $D_\text{–3} = D_3^{\star} = j · B_3/2 = –j · 0.5 V$.