Aufgaben:Aufgabe 1.5Z: Ausfallwahrscheinlichkeiten: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) K (Nabil verschob die Seite Zusatzaufgaben:1.5 Ausfallwahrscheinlichkeiten nach 1.5Z Ausfallwahrscheinlichkeiten) |
|||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Stochastische Signaltheorie/Statistische Abhängigkeit und Unabhängigkeit}} | {{quiz-Header|Buchseite=Stochastische Signaltheorie/Statistische Abhängigkeit und Unabhängigkeit}} | ||
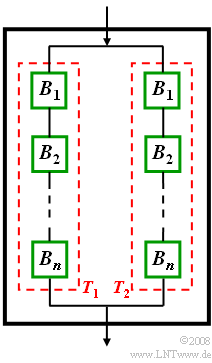
| − | [[Datei:P_ID87__Sto_Z_1_5.png|right|]] | + | [[Datei:P_ID87__Sto_Z_1_5.png|right|Funktionsschaltbild des Gerätes]] |
| − | Ein Geräteteil ist aus den Bauteilen $ | + | Ein Geräteteil ist aus den Bauteilen $B_1, B_2, … , B_n$ aufgebaut, wobei die jeweilige Funktionsfähigkeit unabhängig von allen anderen Bauteilen angenommen werden kann. |
| + | *Das Teil $T_1$ funktioniert nur dann, wenn alle $n$ Bauteile funktionsfähig sind. | ||
| + | *Gehen Sie davon aus, dass alle Bauteile mit gleicher Wahrscheinlichkeit $p_{\rm A}$ ausfallen. | ||
| + | |||
Zur Erhöhung der Zuverlässigkeit werden wichtige Baugruppen häufig dupliziert. Das Gerät $G$ kann somit mengentheoretisch wie folgt beschrieben werden: | Zur Erhöhung der Zuverlässigkeit werden wichtige Baugruppen häufig dupliziert. Das Gerät $G$ kann somit mengentheoretisch wie folgt beschrieben werden: | ||
| − | $$ G = T_1 \cup T_2 $$ | + | $$ G = T_1 \cup T_2.$$ |
Das heißt: Das Gerät $G$ ist bereits dann einsatzbereit, wenn zumindest eines der beiden baugleichen Teilgeräte ($T_1$ oder $T_2$) funktionsfähig ist. | Das heißt: Das Gerät $G$ ist bereits dann einsatzbereit, wenn zumindest eines der beiden baugleichen Teilgeräte ($T_1$ oder $T_2$) funktionsfähig ist. | ||
| − | '' | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit|Statistische Abhängigkeit und Unabhängigkeit]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo: | ||
| + | :[[Statistische Abhängigkeit und Unabhängigkeit]] | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Die Ausfallwahrscheinlichkeit $ | + | {Die Ausfallwahrscheinlichkeit $p_{\rm G}$ des Gesamtgeräts darf nicht größer sein als 0.04%. Wie groß dürfen dann die Ausfallwahrscheinlichkeiten $p_{\rm T}$ der zwei parallel vorhandenen identischen Geräteteile höchstens sein? |
|type="{}"} | |type="{}"} | ||
| − | $p_\text{T,max}$ | + | $p_\text{T, max} \ = $ { 0.02 3% } |
| − | {Die Ausfallwahrscheinlichkeit aller Bauteile sei $ | + | {Die Ausfallwahrscheinlichkeit aller Bauteile sei $p_{\rm A} = 0.1$. Jedes Teilgerät bestehe aus $n = 3$ Bauteilen. Berechnen Sie die Wahrscheinlichkeit $p_{\rm T}$ exakt, dass ein Teilgerät ausfällt. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\text{exakt: }p_{\rm T} \ = $ { 0.271 3% } |
| − | {Welcher Wert ergibt sich für $ | + | {Welcher Wert ergibt sich für $p_{\rm A} = 0.01$? In welcher Form kann man $p_{\rm T}$ für kleine Werte von $p_{\rm A}$ annähern? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\text{Näherung: }p_{\rm T} \ = $ { 0.0297 3% } |
| − | {Nun gelte für die Ausfallwahrscheinlichkeit aller Bauteile $ | + | {Nun gelte für die Ausfallwahrscheinlichkeit aller Bauteile $p_{\rm A} = 0.4\%$. Wieviele Bauteile kann das Teilgerät höchstens enthalten, wenn $p_{\rm T} ≤ 2\%$ gelten soll? |
|type="{}"} | |type="{}"} | ||
| − | $n$ | + | $n \ = $ { 5 3% } |
Version vom 22. Februar 2017, 16:12 Uhr
Ein Geräteteil ist aus den Bauteilen $B_1, B_2, … , B_n$ aufgebaut, wobei die jeweilige Funktionsfähigkeit unabhängig von allen anderen Bauteilen angenommen werden kann.
- Das Teil $T_1$ funktioniert nur dann, wenn alle $n$ Bauteile funktionsfähig sind.
- Gehen Sie davon aus, dass alle Bauteile mit gleicher Wahrscheinlichkeit $p_{\rm A}$ ausfallen.
Zur Erhöhung der Zuverlässigkeit werden wichtige Baugruppen häufig dupliziert. Das Gerät $G$ kann somit mengentheoretisch wie folgt beschrieben werden:
$$ G = T_1 \cup T_2.$$
Das heißt: Das Gerät $G$ ist bereits dann einsatzbereit, wenn zumindest eines der beiden baugleichen Teilgeräte ($T_1$ oder $T_2$) funktionsfähig ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel Statistische Abhängigkeit und Unabhängigkeit.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:
Fragebogen
Musterlösung
- 1. Da die beiden Teilgeräte unabhängig voneinander ausfallen, gilt mengentheoretisch:
- $$\rm Pr(\it G \rm \hspace{0.1cm}f\ddot{a}llt\hspace{0.1cm}aus) = Pr(\it T_{\rm 1}\rm \hspace{0.1cm} f\ddot{a}llt \hspace{0.1cm}aus) \cdot Pr(\it T_{\rm 2}\rm \hspace{0.1cm} f\ddot{a}llt \hspace{0.1cm}aus). $$
- Da die Teilgeräte T1 und T2 baugleich sind, fallen sie mit der gleichen Wahrscheinlichkeit pT aus. Daraus folgt:
- $$\rm \it p_{\rm G} = \it p_{\rm T}^{\rm 2} \hspace{0.5cm} \rm bzw. \hspace{0.5cm} \rm \it p_{\rm T}= \sqrt{\it p_{\rm G}} \le \rm\sqrt{0.0004} \hspace{0.15cm}\underline {= 0.02}.$$
- 2. Dieses Ergebnis ist einfacher über das Komplementärereignis zu bestimmen:
- $$\rm Pr(\it T_{\rm 1}\hspace{0.1cm}\rm funktioniert) = \rm Pr(\it B_{\rm 1} \hspace{0.1cm}\rm funktioniert \cap \it B_{\rm 2} \hspace{0.1cm} \rm funktioniert \cap \it B_{\rm 3}\hspace{0.1cm} \rm funktioniert).$$
- $$\Rightarrow 1- p_{\rm T}= (1-p_{\rm A})^{3} \hspace{0.3cm}\rm \Rightarrow \hspace{0.3cm} 1-p_{\rm T}=(0.9)^3= 0.729 \hspace{0.3cm}\rm \Rightarrow \hspace{0.3cm} p_{\rm T}\hspace{0.15cm}\underline {= 0.271 = 27.1\%}.$$
- 3. Mit pA = 0.01 erhält man pT = 0.0297. Allgemein gilt die Näherung: pT ≈ n · pA (= 3%).
- 4. Mit der Näherung aus (c) folgt direkt n = 5. Bei größerem pA müsste man wie folgt vorgehen:
- $$0.996^{\it n}\ge 0.98 \hspace{0.5cm} \rm\Longrightarrow \hspace{0.5cm} \it n\le\rm\frac{log(0.98)}{log(0.996)} = 5.0406\hspace{0.15cm}\underline { \approx 5}.$$