Aufgaben:Aufgabe 3.8Z: Tupel aus ternären Zufallsgrößen: Unterschied zwischen den Versionen

Version vom 26. November 2016, 18:56 Uhr

Wir betrachten das Tupel $Z = (X, Y)$, wobei die Einzelkomponenten $X$ und $Y$ jeweils ternäre Zufallsgrößen darstellen $\Rightarrow$ Symbolumfang $|X| = |Y| = 3$. Die gemeinsame Wahrscheinlichkeitsfunktion $P_{ XY }(X, Y)$ ist rechts angegeben.

In dieser Aufgabe sind zu berechnen:

die Verbundentropie $H(XY)$ und die Transinformation $I(X; Y)$,
die Verbundentropie $H(XZ)$ und die Transinformation $I(X; Z)$,
die bedingten Entropien $H(Z|X)$ und $H(X|Z)$.

Hinweis: Die Aufgabe bezieht sich auf das Themengebiet von Kapitel 3.2.

Fragebogen

Musterlösung

1. 2. 3. 4. 5. 6. 7.

@@ Zeile 4: / Zeile 4: @@
 }}
-[[Datei:|right|]]
+[[Datei:P_ID2771__Inf_Z_3_7.png|right|]]
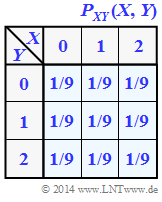
+Wir betrachten das Tupel $Z = (X, Y)$, wobei die Einzelkomponenten $X$ und $Y$ jeweils ternäre Zufallsgrößen darstellen $\Rightarrow$ Symbolumfang $|X| = |Y| = 3$. Die gemeinsame Wahrscheinlichkeitsfunktion $P_{ XY }(X, Y)$ ist rechts angegeben.
+In dieser Aufgabe sind zu berechnen:
+:* die Verbundentropie $H(XY)$ und die Transinformation $I(X; Y)$,
+:*die Verbundentropie $H(XZ)$ und die Transinformation $I(X; Z)$,
+:*die bedingten Entropien $H(Z|X)$ und $H(X|Z)$.
+'''Hinweis:''' Die Aufgabe bezieht sich auf das Themengebiet von [http://www.lntwww.de/Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgr%C3%B6%C3%9Fen Kapitel 3.2].
@@ Zeile 10: / Zeile 19: @@
 <quiz display=simple>
-{Multiple-Choice Frage
+{Berechnen Sie die folgenden Entropien.
-|type="[]"}
-- Falsch
-+ Richtig
-{Input-Box Frage
 |type="{}"}
-$\alpha$ = { 0.3 }
+$ H(X)$ = { 1.585 }