Aufgaben:Aufgabe 3.14: Kanalcodierungstheorem: Unterschied zwischen den Versionen

Version vom 28. November 2016, 22:31 Uhr

Shannons Kanalcodierungstheorem besagt, dass über einen diskreten gedächtnislosen Kanal (DMC) mit der Coderate $R$ fehlerfrei übertragen werden kann, so lange $R$ nicht größer ist als die Kanalkapazität $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ Das Kanalcodierungstheorem soll in dieser Aufgabe numerisch ausgewertet werden, wobei zwei typische Kanalmodelle zu betrachten sind:

das $\text{BSC–Modell}$ (Binary Symmetric Channel) mit Verfälschungswahrscheinlichkeit $ε = 0.25$ und der Kanalkapazität $C = 1 – H_{bin}(ε),$
das sog. $\text{EUC–Modell}$ (Extremely Unsymmetric Channel) entsprechend der Aufgabe Z3.10 (diese Bezeichnung ist nicht allgemein üblich)

Hinweis: Diese Aufgabe gehört zum Themengebiet von Kapitel 3.3. Die Grafiken zeigen die numerischen Werte der informationstheoretischen Größen für die beiden Kanäle „BSC” und „EUC”:

der Quellenentropie $H(X),$
der Äquivokation $H(X|Y),$
der Transinformation $I(X; Y),$
der Irrelevanz $H(Y|X),$ und
der Sinkenentropie $H(Y).$

Der Parameter in diesen Tabellen ist $p_0 = Pr(X = 0)$ im Bereich von $0.3$ bis $0.7.$ Entsprechend gilt für die Wahrscheinlichkeit des Quellensymbols „1”: $p_1 = 1 – p_0$

Fragebogen

Musterlösung

1. 2. 3. 4. 5. 6. 7.

@@ Zeile 3: / Zeile 3: @@
 }}
-[[Datei:|right|]]
+[[Datei:P_ID2817__Inf_A_3_13.png|right|]]
+Shannons Kanalcodierungstheorem besagt, dass über einen diskreten gedächtnislosen Kanal (DMC) mit der Coderate $R$ fehlerfrei übertragen werden kann, so lange $R$ nicht größer ist als die Kanalkapazität
+$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
+Das Kanalcodierungstheorem soll in dieser Aufgabe numerisch ausgewertet werden, wobei zwei typische Kanalmodelle zu betrachten sind:
+:* das $\text{BSC–Modell}$ ''(Binary Symmetric Channel)'' mit Verfälschungswahrscheinlichkeit $ε = 0.25$ und der Kanalkapazität $C = 1 – H_{bin}(ε),$
+:* das sog. $\text{EUC–Modell}$ ''(Extremely Unsymmetric Channel)'' entsprechend der [http://www.lntwww.de/Aufgaben:3.10Z_Extrem_unsymmetrischer_Kanal Aufgabe Z3.10] (diese Bezeichnung ist nicht allgemein üblich)
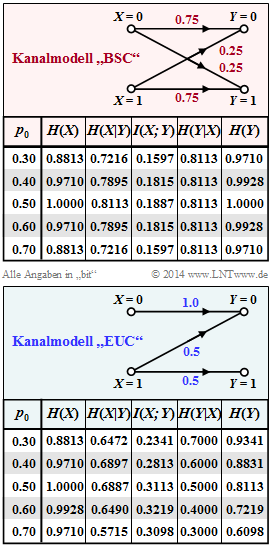
+'''Hinweis:''' Diese Aufgabe gehört zum Themengebiet von [http://www.lntwww.de/Informationstheorie/Anwendung_auf_die_Digitalsignal%C3%BCbertragung Kapitel 3.3]. Die Grafiken zeigen die numerischen Werte der informationstheoretischen Größen für die beiden Kanäle „BSC” und „EUC”:
+:* der Quellenentropie $H(X),$
+:* der Äquivokation $H(X|Y),$
+:* der Transinformation $I(X; Y),$
+:* der Irrelevanz $H(Y|X),$ und
+:* der Sinkenentropie $H(Y).$
+Der Parameter in diesen Tabellen ist $p_0 = Pr(X = 0)$ im Bereich von $0.3$ bis $0.7.$ Entsprechend gilt für die Wahrscheinlichkeit des Quellensymbols „1”:  $p_1 = 1 – p_0$

	Falsch
	Richtig