Aufgaben:Aufgabe 1.2: Verzerrungen? Oder keine Verzerrung?: Unterschied zwischen den Versionen

Version vom 11. Dezember 2016, 17:42 Uhr

Die drei Nachrichtensysteme $S_1$, $S_2$ und $S_3$ werden hinsichtlich der durch sie verursachten Verzerrungen analysiert. Zu diesem Zwecke wird an den Eingang eines jeden Systems das cosinusförmige Testsignal $$q(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )$$ angelegt. Die Signalfrequenz ist stets $f_N = 1 kHz$.

Gemessen werden die Signale am Ausgang der drei Systeme, die in der Grafik dargestellt sind: $$v_1(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )\hspace{0.05cm}$$ $$v_2(t) = 1 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t)$$ $$ + 1 \;{\rm V} \cdot \sin(2 \pi f_{\rm N} t) \hspace{0.05cm},$$ $$v_3(t)= 1.5 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t)$$ $$- 0.3 \;{\rm V} \cdot \cos(6 \pi f_{\rm N} t)\hspace{0.05cm}.$$

Anzumerken ist, dass hier die in der Praxis stets vorhandenen Rauschanteile als vernachlässigbar klein angenommen werden.

Hinweis:Diese Aufgabe bezieht sich auf das Kapitel 1.2 des vorliegenden Buches und das Kapitel 2.2 von „Lineare zeitinvariante Systeme”. Bei nichtlinearen Verzerrungen ist das Sinken–$\text{SNR}$ $ρ_υ = 1/K^{ 2 }$, wobei der Klirrfaktor $K$ das Verhältnis der Effektivwerte aller Oberwellen und Grundfrequenz angibt.

Fragebogen

Musterlösung

1. 2. 3. 4. 5. 6. 7.

@@ Zeile 3: / Zeile 3: @@
 }}
-[[Datei:|right|]]
+[[Datei:P_ID949__Mod_A_1_2.png|right|]]
+Die drei Nachrichtensysteme $S_1$, $S_2$ und $S_3$ werden hinsichtlich der durch sie verursachten Verzerrungen analysiert. Zu diesem Zwecke wird an den Eingang eines jeden Systems das cosinusförmige Testsignal
+$$q(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )$$
+angelegt. Die Signalfrequenz ist stets $f_N = 1 kHz$.
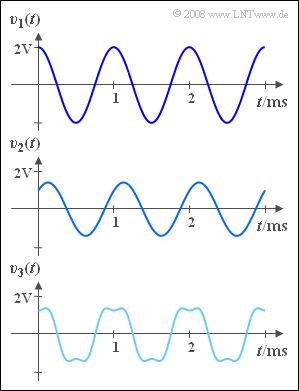
+Gemessen werden die Signale am Ausgang der drei Systeme, die in der Grafik dargestellt sind:
+$$v_1(t) =  2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )\hspace{0.05cm}$$
+$$v_2(t) =  1 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t)$$
+$$ +  1 \;{\rm V} \cdot \sin(2 \pi f_{\rm N} t) \hspace{0.05cm},$$
+$$v_3(t)=  1.5 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t)$$
+$$- 0.3 \;{\rm V} \cdot \cos(6 \pi f_{\rm N} t)\hspace{0.05cm}.$$
+Anzumerken ist, dass hier die in der Praxis stets vorhandenen Rauschanteile als vernachlässigbar klein angenommen werden.
+'''Hinweis:'''Diese Aufgabe bezieht sich auf das [http://www.lntwww.de/Modulationsverfahren/Qualit%C3%A4tskriterien Kapitel 1.2] des vorliegenden Buches und das [http://www.lntwww.de/Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen Kapitel 2.2] von „Lineare zeitinvariante Systeme”. Bei nichtlinearen Verzerrungen ist das Sinken–$\text{SNR}$ $ρ_υ = 1/K^{ 2 }$, wobei der Klirrfaktor $K$ das Verhältnis der Effektivwerte aller Oberwellen und Grundfrequenz angibt.

	Falsch
	Richtig