Aufgaben:Aufgabe 1.3: Systemvergleich beim AWGN–Kanal: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Qualitätskriterien }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type=…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID960__Mod_A_1_3.png|right|]] |
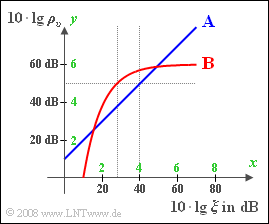
| + | Für den Vergleich verschiedener Modulationsverfahren und Demodulatoren hinsichtlich der Rauschempfindlichkeit gehen wir meist vom so genannten $\text{AWGN}$–Kanal aus und beschreiben folgendes doppelt–logarithmische Diagramm: | ||
| + | :*Die Ordinate gibt den Sinken–Störabstand (SNR logarithmiert) $10 · lg ρ_υ$ in dB an. | ||
| + | :*Auf der Abszisse ist $10 · lg ξ$ aufgetragen, wobei für die normierte Leistungskenngröße gilt: | ||
| + | $$ \xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$ | ||
| + | :*In $ξ$ sind also die Sendeleistung $P_S$, der Kanaldämpfungsfaktor $α_K$, die Rauschleistungsdichte $N_0$ sowie die Bandbreite $B_{NF}$ des Nachrichtensignals in geeigneter Weise zusammengefasst. | ||
| + | :* Wenn nicht ausdrücklich etwas anderes angegeben ist, soll in der Aufgabe von folgenden Werten ausgegangen werden: | ||
| + | $$ P_{\rm S}= 5 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm K} = 0.001\hspace{0.05cm}, \hspace{0.2cm} {N_0} = 10^{-10}\;\frac{{\rm W}}{{\rm Hz}}\hspace{0.05cm}, \hspace{0.2cm} B_{\rm NF}= 5\; {\rm kHz}\hspace{0.05cm}.$$ | ||
| + | In der Grafik sind zwei Systeme eingezeichnet, deren (x, y)–Verlauf wie folgt beschrieben werden kann: | ||
| + | :*'''System A:''' | ||
| + | $y = x+1$ | ||
| + | :*'''System B:''' | ||
| + | $$ y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right)\hspace{0.05cm}.$$ | ||
| + | Die in der Grafik zusätzlich grün eingezeichneten Achsenbeschriftungen haben folgende Bedeutung: | ||
| + | $$ x = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\xi} {10 \,{\rm dB}}\hspace{0.05cm}, \hspace{0.3cm}y = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\rho_v} {10 \,{\rm dB}}\hspace{0.05cm}.$$ | ||
| + | So steht $x = 4$ für $10 · lg ξ = 40$ dB bzw. $ξ = 104$ und $y = 5$ für $10 · lg ρυ = 50$ dB, also $ρ_υ = 105$. | ||
| + | |||
| + | '''Hinweis:'''Diese Aufgabe bezieht sich auf den Theorieteil von [http://www.lntwww.de/Modulationsverfahren/Qualit%C3%A4tskriterien Kapitel 1.2]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 12. Dezember 2016, 14:12 Uhr
Für den Vergleich verschiedener Modulationsverfahren und Demodulatoren hinsichtlich der Rauschempfindlichkeit gehen wir meist vom so genannten $\text{AWGN}$–Kanal aus und beschreiben folgendes doppelt–logarithmische Diagramm:
- Die Ordinate gibt den Sinken–Störabstand (SNR logarithmiert) $10 · lg ρ_υ$ in dB an.
- Auf der Abszisse ist $10 · lg ξ$ aufgetragen, wobei für die normierte Leistungskenngröße gilt:
$$ \xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$
- In $ξ$ sind also die Sendeleistung $P_S$, der Kanaldämpfungsfaktor $α_K$, die Rauschleistungsdichte $N_0$ sowie die Bandbreite $B_{NF}$ des Nachrichtensignals in geeigneter Weise zusammengefasst.
- Wenn nicht ausdrücklich etwas anderes angegeben ist, soll in der Aufgabe von folgenden Werten ausgegangen werden:
$$ P_{\rm S}= 5 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm K} = 0.001\hspace{0.05cm}, \hspace{0.2cm} {N_0} = 10^{-10}\;\frac[[:Vorlage:\rm W]][[:Vorlage:\rm Hz]]\hspace{0.05cm}, \hspace{0.2cm} B_{\rm NF}= 5\; {\rm kHz}\hspace{0.05cm}.$$ In der Grafik sind zwei Systeme eingezeichnet, deren (x, y)–Verlauf wie folgt beschrieben werden kann:
- System A:
$y = x+1$
- System B:
$$ y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right)\hspace{0.05cm}.$$ Die in der Grafik zusätzlich grün eingezeichneten Achsenbeschriftungen haben folgende Bedeutung: $$ x = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\xi} {10 \,{\rm dB}}\hspace{0.05cm}, \hspace{0.3cm}y = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\rho_v} {10 \,{\rm dB}}\hspace{0.05cm}.$$ So steht $x = 4$ für $10 · lg ξ = 40$ dB bzw. $ξ = 104$ und $y = 5$ für $10 · lg ρυ = 50$ dB, also $ρ_υ = 105$.
Hinweis:Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.2.
Fragebogen
Musterlösung