Aufgaben:Aufgabe 1.3Z: Thermisches Rauschen: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 5: | Zeile 5: | ||
[[Datei:P_ID953__Mod_Z_1_3.png|right|]] | [[Datei:P_ID953__Mod_Z_1_3.png|right|]] | ||
Eine fundamentale und bei jedem Nachrichtensystem auftretende Störung ist das thermische Rauschen, da jeder Widerstand $R$ mit der absoluten Temperatur $θ$ (in „Grad Kelvin”) ein Rauschsignal $n(t)$ mit der (einseitigen) Rauschleistungsdichte | Eine fundamentale und bei jedem Nachrichtensystem auftretende Störung ist das thermische Rauschen, da jeder Widerstand $R$ mit der absoluten Temperatur $θ$ (in „Grad Kelvin”) ein Rauschsignal $n(t)$ mit der (einseitigen) Rauschleistungsdichte | ||
| − | $$ | + | $$N_{0,min} = k_B \cdot \theta ( k_B = 1.38 \cdot 10^{ -23 } Ws/K)$$ |
abgibt. $k_B$ bezeichnet man als die Boltzmann–Konstante. | abgibt. $k_B$ bezeichnet man als die Boltzmann–Konstante. | ||
| Zeile 20: | Zeile 20: | ||
Die zweiseitige Rauschleistungsdichte von bandbegrenztem Tiefpass–Rauschen $n_{TP}(t)$ lautet: | Die zweiseitige Rauschleistungsdichte von bandbegrenztem Tiefpass–Rauschen $n_{TP}(t)$ lautet: | ||
$$ {\it \Phi}_{n, {\hspace{0.05cm}\rm TP}}(f) = \left\{ \begin{array}{c} N_0/2 \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < B,} \\ {\rm sonst.} \\ \end{array}$$ | $$ {\it \Phi}_{n, {\hspace{0.05cm}\rm TP}}(f) = \left\{ \begin{array}{c} N_0/2 \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < B,} \\ {\rm sonst.} \\ \end{array}$$ | ||
| − | + | Dagegen gilt bei bandpassartigem Rauschen $n_{BP}(t)$ mit der Mittenfrequenz $f_M$: | |
| + | $${\it \Phi}_{n, {\hspace{0.05cm}\rm BP}}(f) = \left\{ \begin{array}{c} N_0/2 \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f - f_{\rm M}\hspace{0.05cm} \right| < B/2,} \\ {\rm sonst.} \\ \end{array}.$$ | ||
| + | Für alle nachfolgenden numerischen Berechnungen wird vorausgesetzt: | ||
| + | $$ F = 10, \hspace{0.2cm}\theta = 290\,{\rm K},\hspace{0.2cm}R = 50\,{\rm \Omega},\hspace{0.2cm}B = 30\,{\rm kHz},\hspace{0.2cm}f_{\rm M} = 0 \hspace{0.1cm}{\rm bzw.}\hspace{0.1cm}100\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf die theoretischen Grundlagen von [http://www.lntwww.de/Modulationsverfahren/Qualit%C3%A4tskriterien Kapitel 1.2]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 15. Dezember 2016, 00:16 Uhr
Eine fundamentale und bei jedem Nachrichtensystem auftretende Störung ist das thermische Rauschen, da jeder Widerstand $R$ mit der absoluten Temperatur $θ$ (in „Grad Kelvin”) ein Rauschsignal $n(t)$ mit der (einseitigen) Rauschleistungsdichte $$N_{0,min} = k_B \cdot \theta ( k_B = 1.38 \cdot 10^{ -23 } Ws/K)$$ abgibt. $k_B$ bezeichnet man als die Boltzmann–Konstante.
Allerdings ist diese aus physikalischen Gründen auf $6$ $\text{THz}$ begrenzt. Weiterhin ist zu beobachten, dass dieser minimale Wert nur bei exakter Widerstandsanpassung erreicht werden kann.
Bei der Realisierung einer Schaltungseinheit – zum Beispiel eines Verstärkers – ist die wirksame Rauschleistungsdichte meist deutlich größer, da sich mehrere Rauschquellen addieren und zudem Fehlanpassungen eine Rolle spielen. Dieser Effekt wird durch die Rauschzahl F erfasst, und es gilt: $$ N_0 = F \cdot {N_{\rm 0, \hspace{0.05cm}min}}= F \cdot k_{\rm B} \cdot \theta \hspace{0.05cm}.$$ Für die wirksame Rauschleistung gilt mit der Bandbreite $B$: $$N = N_0 \cdot B \hspace{0.1cm}\left(= N_0 \cdot B\cdot R = \sigma_n^2\right) \hspace{0.01cm}.$$ Nach der ersten Gleichung ergibt sich die tatsächliche, physikalische Leistung in „W”. Nach der zweiten, in Klammern angegebenen Gleichung hat das Ergebnis die Einheit „$V^{ 2 }$”. Das heißt: Hier ist die Leistung – wie in der Nachrichtentechnik allgemein üblich – auf den Bezugswiderstand $\text{R = 1 Ω}$ umgerechnet. Diese Gleichung muss auch herangezogen werden, um den Effektivwert (die Streuung) σn des Rauschsignals $n(t)$ zu berechnen.
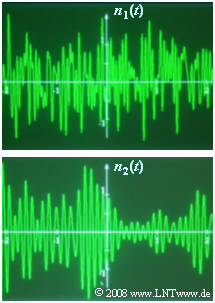
Alle Gleichungen gelten unabhängig davon, ob es sich um Tiefpass– oder Bandpass–Rauschen handelt. Die Grafik zeigt zwei Rauschsignale $n_1(t)$ und $n_2(t)$ bei gleicher Bandbreite. In der Teilaufgabe (d) ist gefragt, welches dieser Signale am Ausgang eines Tiefpasses bzw. eines Bandpasses auftreten wird.
Die zweiseitige Rauschleistungsdichte von bandbegrenztem Tiefpass–Rauschen $n_{TP}(t)$ lautet: $$ {\it \Phi}_{n, {\hspace{0.05cm}\rm TP}}(f) = \left\{ \begin{array}{c} N_0/2 \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < B,} \\ {\rm sonst.} \\ \end{array}$$ Dagegen gilt bei bandpassartigem Rauschen $n_{BP}(t)$ mit der Mittenfrequenz $f_M$: $${\it \Phi}_{n, {\hspace{0.05cm}\rm BP}}(f) = \left\{ \begin{array}{c} N_0/2 \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f - f_{\rm M}\hspace{0.05cm} \right| < B/2,} \\ {\rm sonst.} \\ \end{array}.$$ Für alle nachfolgenden numerischen Berechnungen wird vorausgesetzt: $$ F = 10, \hspace{0.2cm}\theta = 290\,{\rm K},\hspace{0.2cm}R = 50\,{\rm \Omega},\hspace{0.2cm}B = 30\,{\rm kHz},\hspace{0.2cm}f_{\rm M} = 0 \hspace{0.1cm}{\rm bzw.}\hspace{0.1cm}100\,{\rm kHz}\hspace{0.05cm}.$$ Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 1.2.
Fragebogen
Musterlösung