Digitalsignalübertragung/Lineare digitale Modulation – Kohärente Demodulation: Unterschied zwischen den Versionen
Aus LNTwww
Ayush (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{Header |Untermenü=Digitalsignalübertragung bei idealisierten Bedingungen |Vorherige Seite=Optimierung der Basisbandübertragungssysteme |Nächste Seite=G…“) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 7: | Zeile 7: | ||
| + | == Gemeinsames Blockschaltbild für ASK und BPSK == | ||
| + | <br> | ||
| + | Im Kapitel 4.2 des Buches „Modulationsverfahren” wurden die digitalen Trägerfrequenzsysteme [http://www.lntwww.de/Modulationsverfahren/Lineare_digitale_Modulationsverfahren#ASK_.E2.80.93_Amplitude_Shift_Keying ASK] (<i>Amplitude Shift Keying</i>) und [http://www.lntwww.de/Modulationsverfahren/Lineare_digitale_Modulationsverfahren#BPSK_.E2.80.93_Binary_Phase_Shift_Keying BPSK] (<i>Binary Phase Shift Keying</i>) bereits ausführlich beschrieben. In diesem Kapitel wird nun die Fehlerwahrscheinlichkeit dieser Systeme berechnet, wobei von dem folgenden gemeinsamen Blockschaltbild ausgegangen wird: | ||
| + | <br><br>[[Datei:P_ID1671__Dig_T_4_1_S1_v3.png|Blockschaltbild eines ASK– und BPSK–Übertragungssystems|class=fit]]<br><br> | ||
| + | Wie im Kapitel 4.2 des Buches „Modulationsverfahren” gelten auch hier folgende Voraussetzungen: | ||
| + | *Die Demodulation geschieht stets <font color="#cc0000"><span style="font-weight: bold;">kohärent</span></font>. Das heißt: Beim Empfänger wird ein Trägersignal mit gleicher Frequenz wie beim Sender zugesetzt, aber mit doppelter Amplitude. Der Phasenversatz sei zunächst Δ<i>ϕ</i><sub>T</sub> = 0.<br> | ||
| + | *Bei BPSK wird von den bipolaren Amplitudenkoeffizienten <i>a<sub>ν</sub></i> ∈ {–1, +1} ausgegangen und die Entscheiderschwelle liegt bei <i>E</i> = 0. Dagegen gilt bei ASK <i>a<sub>ν</sub></i> ∈ {0, 1}. Die Entscheiderschwelle <i>E</i> ist für diesen unipolaren Fall bestmöglich zu wählen.<br> | ||
| + | *Wir betrachten stets den AWGN–Kanal, das heißt, dass für den Kanalfrequenzgang <i>H</i><sub>K</sub>(<i>f</i>) = 1 gilt und <i>n</i>(<i>t</i>) weißes Gaußsches Rauschen mit der (einseitigen) Rauschleistungsdichte <i>N</i><sub>0</sub> darstellt.<br> | ||
| + | *Die Entzerrung linearer Kanalverzerrungen – also der Fall <i>H</i><sub>K</sub>(<i>f</i>) ≠ const. – ist in gleicher Weise möglich wie bei der Basisbandübertragung. Hierzu sei auf das Kapitel 3.3 verwiesen.<br> | ||
| − | + | <math></math><br> | |
| − | + | <br> | |
| + | <br><br> | ||
| + | [[Datei:||class=fit]]<br><br> | ||
Version vom 19. Dezember 2016, 16:44 Uhr
Gemeinsames Blockschaltbild für ASK und BPSK
Im Kapitel 4.2 des Buches „Modulationsverfahren” wurden die digitalen Trägerfrequenzsysteme ASK (Amplitude Shift Keying) und BPSK (Binary Phase Shift Keying) bereits ausführlich beschrieben. In diesem Kapitel wird nun die Fehlerwahrscheinlichkeit dieser Systeme berechnet, wobei von dem folgenden gemeinsamen Blockschaltbild ausgegangen wird:
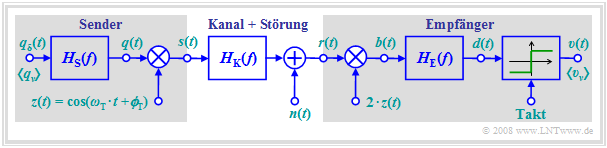
Wie im Kapitel 4.2 des Buches „Modulationsverfahren” gelten auch hier folgende Voraussetzungen:
- Die Demodulation geschieht stets kohärent. Das heißt: Beim Empfänger wird ein Trägersignal mit gleicher Frequenz wie beim Sender zugesetzt, aber mit doppelter Amplitude. Der Phasenversatz sei zunächst ΔϕT = 0.
- Bei BPSK wird von den bipolaren Amplitudenkoeffizienten aν ∈ {–1, +1} ausgegangen und die Entscheiderschwelle liegt bei E = 0. Dagegen gilt bei ASK aν ∈ {0, 1}. Die Entscheiderschwelle E ist für diesen unipolaren Fall bestmöglich zu wählen.
- Wir betrachten stets den AWGN–Kanal, das heißt, dass für den Kanalfrequenzgang HK(f) = 1 gilt und n(t) weißes Gaußsches Rauschen mit der (einseitigen) Rauschleistungsdichte N0 darstellt.
- Die Entzerrung linearer Kanalverzerrungen – also der Fall HK(f) ≠ const. – ist in gleicher Weise möglich wie bei der Basisbandübertragung. Hierzu sei auf das Kapitel 3.3 verwiesen.
\(\)
[[Datei:||class=fit]]