Digitalsignalübertragung/Symbolweise Codierung mit Pseudoternärcodes: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{Header |Untermenü=Codierte und mehrstufige Übertragung |Vorherige Seite=Blockweise Codierung mit 4B3T-Codes |Nächste Seite=Ursachen und Auswirkungen von…“) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 24: | Zeile 24: | ||
Die Bildbeschreibung folgt auf der nächsten Seite.<br> | Die Bildbeschreibung folgt auf der nächsten Seite.<br> | ||
| + | |||
| + | |||
| + | == Allgemeine Beschreibung von Partial Response Codes (2) == | ||
| + | <br> | ||
| + | Die Beschreibung des <i>Partial Response Coders</i> wird fortgesetzt: | ||
| + | |||
| + | [[Datei:P_ID1343__Dig_T_2_4_S1_v1.png|Block- und Ersatzschaltbild eines Pseudoternärcodes|class=fit]]<br><br> | ||
| + | |||
| + | Man erkennt aus den beiden Darstellungen (Blockschaltbild links, Ersatzschaltbild rechts): | ||
| + | *Der Pseudoternärcoder kann in den nichtlinearen Vorcodierer und ein lineares Codiernetzwerk aufgespalten werden, wenn man die Verzögerung um <i>N</i><sub>C</sub> · <i>T</i> und die Gewichtung mit <i>K</i><sub>C</sub> zur Verdeutlichung zweimal zeichnet.<br> | ||
| + | |||
| + | *Der nichtlineare Vorcodierer gewinnt durch eine Modulo–2–Addition (Antivalenz) zwischen den Symbolen <i>q<sub>ν</sub></i> und <i>K</i><sub>C</sub> · <i>b</i><sub><i>ν</i>–<i>N</i>c</sub> die vorcodierten Symbole <i>b<sub>ν</sub></i>, die ebenfalls binär sind: | ||
| + | |||
| + | ::<math>q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, | ||
| + | +1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, | ||
| + | +1\}\hspace{0.05cm}.</math> | ||
| + | |||
| + | *Die Symbole <i>b<sub>ν</sub></i> sind wie die Quellensymbole <i>q<sub>ν</sub></i> statistisch voneinander unabhängig. Durch den Vorcodierer wird also keine Redundanz hinzugefügt. Er gestattet aber eine einfache Realisierung des Decoders und verhindert eine Fehlerfortpflanzung nach einem Übertragungsfehler.<br> | ||
| + | |||
| + | *Die eigentliche Umcodierung von binär auf ternär bewirkt das lineare Codiernetzwerk durch die herkömmliche Subtraktion | ||
| + | |||
| + | ::<math>c(t) ={1}/{2} \cdot \left [b(t) - K_{\rm C} \cdot b(t- N_{\rm | ||
| + | C}\cdot T)\right] \hspace{0.05cm}.</math> | ||
| + | |||
| + | :Dieses ternäre Signal (Stufenzahl <i>M</i> = 3) weist die normierten Werte <i>a<sub>ν</sub></i> ∈ {–1, 0, +1} auf.<br> | ||
| + | |||
| + | *Weiterhin gilt für das (nun redundante) Sendesignal <i>s</i>(<i>t</i>) mit dem Sendegrundimpuls <i>g<sub>s</sub></i>(<i>t</i>), der im gesamten Kapitel 2.4 stets als NRZ–Rechteck vorausgesetzt wird: | ||
| + | |||
| + | ::<math>s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.05cm}.</math> | ||
| + | |||
| + | *Die relative Coderedundanz ist für alle Pseudoternärcodes gleich <i>r<sub>c</sub></i> = 1 – 1/log<sub>2</sub>(3) ≈ 36.9 %.<br> | ||
<math></math><br> | <math></math><br> | ||
Version vom 21. Dezember 2016, 16:40 Uhr
Allgemeine Beschreibung von Partial Response Codes (1)
Bei der symbolweisen Codierung wird mit jedem ankommenden Quellensymbol qν ein Codesymbol cν erzeugt, das außer vom aktuellen Eingangssymbol qν auch von den NC vorangegangenen Symbolen abhängt. NC bezeichnet man als die
Ordnung des Codes.
Typisch für eine symbolweise Codierung ist, dass
- die Symboldauer T des Codersignals (und des Sendesignals) mit der Bitdauer TB des binären Quellensignals übereinstimmt,
- Codierung und Decodierung nicht zu größeren Zeitverzögerungen führen, die bei Verwendung von Blockcodes unvermeidbar sind.
Besondere Bedeutung besitzen die Pseudomehrstufencodes – besser bekannt unter der englischen Bezeichnung Partial Response Codes.
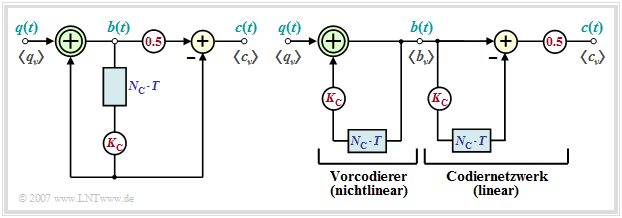
Im Folgenden werden ausschließlich die Pseudoternärcodes mit der Stufenzahl M = 3 betrachtet, die durch das Blockschaltbild entsprechend der linken Grafik beschreibbar sind. In der rechten Grafik ist ein Ersatzschaltbild angegeben, das für eine Analyse dieser Codes sehr gut geeignet ist.
Die Bildbeschreibung folgt auf der nächsten Seite.
Allgemeine Beschreibung von Partial Response Codes (2)
Die Beschreibung des Partial Response Coders wird fortgesetzt:
Man erkennt aus den beiden Darstellungen (Blockschaltbild links, Ersatzschaltbild rechts):
- Der Pseudoternärcoder kann in den nichtlinearen Vorcodierer und ein lineares Codiernetzwerk aufgespalten werden, wenn man die Verzögerung um NC · T und die Gewichtung mit KC zur Verdeutlichung zweimal zeichnet.
- Der nichtlineare Vorcodierer gewinnt durch eine Modulo–2–Addition (Antivalenz) zwischen den Symbolen qν und KC · bν–Nc die vorcodierten Symbole bν, die ebenfalls binär sind:
- \[q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, +1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, +1\}\hspace{0.05cm}.\]
- Die Symbole bν sind wie die Quellensymbole qν statistisch voneinander unabhängig. Durch den Vorcodierer wird also keine Redundanz hinzugefügt. Er gestattet aber eine einfache Realisierung des Decoders und verhindert eine Fehlerfortpflanzung nach einem Übertragungsfehler.
- Die eigentliche Umcodierung von binär auf ternär bewirkt das lineare Codiernetzwerk durch die herkömmliche Subtraktion
- \[c(t) ={1}/{2} \cdot \left [b(t) - K_{\rm C} \cdot b(t- N_{\rm C}\cdot T)\right] \hspace{0.05cm}.\]
- Dieses ternäre Signal (Stufenzahl M = 3) weist die normierten Werte aν ∈ {–1, 0, +1} auf.
- Weiterhin gilt für das (nun redundante) Sendesignal s(t) mit dem Sendegrundimpuls gs(t), der im gesamten Kapitel 2.4 stets als NRZ–Rechteck vorausgesetzt wird:
- \[s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.05cm}.\]
- Die relative Coderedundanz ist für alle Pseudoternärcodes gleich rc = 1 – 1/log2(3) ≈ 36.9 %.
\(\)
[[Datei:||class=fit]]