Digitalsignalübertragung/Impulsinterferenzen bei mehrstufiger Übertragung: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 108: | Zeile 108: | ||
*Dagegen ergeben sich für <i>a</i><sub>∗</sub> ≥ 50 dB günstigere Verhältnisse für die Quaternärübertragung. Bei 80 dB Kabeldämpfung ist der Störabstandsgewinn gegenüber <i>M</i> = 2 größer als 3 dB.<br> | *Dagegen ergeben sich für <i>a</i><sub>∗</sub> ≥ 50 dB günstigere Verhältnisse für die Quaternärübertragung. Bei 80 dB Kabeldämpfung ist der Störabstandsgewinn gegenüber <i>M</i> = 2 größer als 3 dB.<br> | ||
| + | == Augenöffnung bei den Pseudoternärcodes (1) == | ||
| + | <br> | ||
| + | In Kapitel 2.4 wurden die Pseudoternärcodes allgemein beschrieben und es wurden für diese die Augendiagramme bei Nyquistimpulsformung angegeben. In der Grafik auf dieser Seite sehen Sie die Augendiagramme – jeweils ohne Rauschen – für den AMI–Code (links) und den Duobinärcode (rechts) im Vergleich zum redundanzfreien Binärcode (Mitte). Die Amplitude ist jeweils zu <i>s</i><sub>0</sub> = 1 normiert.<br> | ||
| + | [[Datei:P ID1416 Dig T 3 4 S4 version1.png|Augendiagramme der Pseudoternärcodes (AMI–Code, Duobinärcode)|class=fit]]<br> | ||
| + | Alle Augendiagramme gelten für ein gaußförmiges Empfangsfilter mit der Grenzfrequenz <i>f</i><sub>G</sub> · <i>T</i> = 0.4, woraus sich folgende (normierte) Grundimpulswerte ergeben: | ||
| + | :<math>g_{0} \approx 0.68, \hspace{0.2cm} g_{1}= g_{-1} \approx 0.16, \hspace{0.2cm}\hspace{0.2cm} g_{2}= g_{-2}= ... \approx 0 \hspace{0.05cm}.</math> | ||
| + | |||
| + | Beim redundanzfreien Binärsystem (mittlere Grafik) erhält man somit für die Augenöffnung | ||
| + | |||
| + | :<math>{\ddot{o}(T_{\rm D})}= 2 \cdot (g_0 - 2 \cdot g_1 ) = 0.72 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | \ddot{o}_{\rm norm} = \frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = 0.36</math> | ||
| + | |||
| + | im Vergleich zu <i>ö</i>(<i>T</i><sub>D</sub>) = 2 bzw. <i>ö</i><sub>norm</sub> = 1 beim binären Nyquistsystem.<br> | ||
| + | |||
| + | Da die Pseudoternärcodes mit der gleichen Symbolrate arbeiten wie das redundanzfreie Binärsystem, | ||
| + | *sind die Detektionsgrundimpulswerte <i>g</i><sub>ν</sub> und auch der Rauscheffektivwert <i>σ<sub>d</sub></i> in allen Fällen gleich,<br> | ||
| + | |||
| + | *ist die (halbe) Augenöffnung für die Systemoptimierung ebenso geeignet wie das S/N–Verhältnis <i>ρ</i><sub>U</sub> = [<i>ö</i>(<i>T</i><sub>D</sub>)/2]<sup>2</sup>/<i>σ<sub>d</sub></i><sup>2</sup> und die daraus resultierende (ungünstigste) Fehlerwahrscheinlichkeit <i>p</i><sub>U</sub>.<br><br> | ||
| + | |||
| + | Die Beschreibung der beiden äußeren Augendiagramme folgt auf der nächsten Seite.<br> | ||
| + | |||
| + | == == | ||
{{Display}} | {{Display}} | ||
Version vom 26. Dezember 2016, 19:14 Uhr
Inhaltsverzeichnis
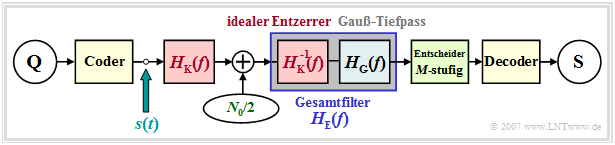
Augenöffnung bei redundanzfreien Mehrstufensystemen (1)
Wir gehen weiterhin von folgenden Voraussetzungen aus:
- NRZ–Rechteck–Sendeimpulse,
- Koaxialkabel und AWGN–Rauschen,
- ideale Kanalentzerrung, sowie
- ein Gaußtiefpass zur Rauschleistungsbegrenzung.
Im Unterschied zu Kapitel 3.3 ist das weiterhin redundanzfreie Sendesignal s(t) nun nicht mehr binär, sondern M–stufig, was sich nur im Wertevorrat der Amplitudenkoeffizienten auswirkt:
\[s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.3cm}{\rm mit}\hspace{0.3cm} a_\nu \in \{ a_1, ... , a_\mu , ... , a_{M}\}\hspace{0.05cm}.\]
Dementsprechend besitzt der Entscheider nun nicht mehr nur eine, sondern M – 1 Entscheiderschwellen und im Augendiagramm sind bei geöffnetem Auge M – 1 Augenöffnungen erkennbar.
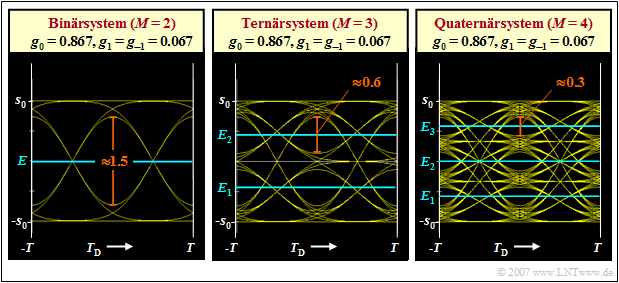
Vergleicht man die Augendiagramme (ohne Rauschen)
- eines binären (M = 2),
- eines ternären (M = 3), und
- eines quaternären (M = 4)
Übertragungssystems bei gleichem vorgegebenen Detektionsgrundimpuls gd(t) und gleicher Symboldauer T, so erhält man für die halbe vertikale Augenöffnung allgemein:
\[{\ddot{o}(T_{\rm D})}/{ 2} = \frac{g_0}{ M-1} - \sum_{\nu = 1}^{\infty} |g_{-\nu} | - \sum_{\nu = 1}^{\infty} |g_{\nu} |\hspace{0.05cm}.\]
Hierbei bezeichnet g0 = gd(t = 0) wie im Kapitel 3.3 den Hauptwert, während die beiden Summen in obiger Gleichung
- die Vorläufer g1, g2, ... (zweiter Term), und
- die Nachläufer g–1, g–2, ... (dritter Term)
berücksichtigen. Dabei gilt stets gν = gd(t = ν · T).
Auf der nächsten Seite wird diese Gleichung an einem Beispiel verdeutlicht.
Augenöffnung bei redundanzfreien Mehrstufensystemen (2)
\[{\ddot{o}(T_{\rm D})}= 2 \cdot (g_0 - 2 \cdot g_1) \approx 1.5 \cdot s_0 \hspace{0.05cm}.\]
Bei den Mehrstufensystemen ist die Augenöffnung per se um den Faktor 1/(M – 1) kleiner. Dadurch wird hier die Augenöffnung durch die (gleich großen) Vor– und Nachläufer (relativ gesehen) stärker verringert als beim Binärsystem. Man erhält bei gleichen Grundimpulswerten für
\[M = 3 : \hspace{0.2cm}{\ddot{o}(T_{\rm D})} = 2 \cdot (g_0/2 - 2 \cdot g_1) \approx 0.6 \cdot s_0 \hspace{0.05cm},\] \[ M = 4 : \hspace{0.2cm}{\ddot{o}(T_{\rm D})} = 2 \cdot (g_0/3 - 2 \cdot g_1) \approx 0.3 \cdot s_0 \hspace{0.05cm}.\]
Anzumerken ist, dass auch für diese beiden Mehrstufensysteme jeweils die normierte Grenzfrequenz <nobr>fG · T = 0.6</nobr> zugrundeliegt. Bei einem Systemvergleich ist allerdings zu beachten, dass sich durch die größere Stufenzahl auch der Informationsfluss erhöht. Das heißt, dass die Mehrstufensysteme besser sind, als es diese Grafiken aussagen. Mehr darüber auf der nächsten Seite.
Vergleich zwischen Binär– und Quaternärsystem (1)
Der auf der letzten Seite angestellte Vergleich ist nicht fair, da nicht von gleichem Informationsfluss ausgegangen wurde. Ein Systemvergleich bei konstanter äquivalenter Bitrate RB muss vielmehr auch berücksichtigen, dass bei den (redundanzfreien) Mehrstufensystemen die Symboldauer T um den Faktor ld (M) größer ist als beim Binärsystem, was sich günstig auf die Impulsinterferenzen auswirkt.
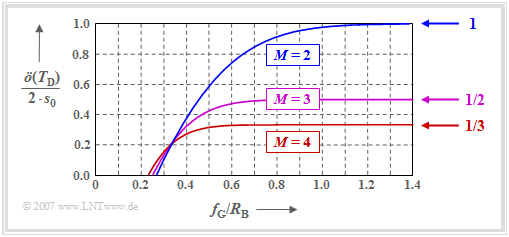
Die Grafik zeigt die (auf s0 normierte) halbe Augenöffnung in Abhängigkeit des Quotienten fG/RB des gaußförmigen Empfangsfilters. In der Aufgabe Z3.4 wird diese in analytischer Form wie folgt berechnet:
\[\ddot{o}_{\rm norm} = \frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = \frac{M}{ M-1}\cdot \frac{g_0}{ s_0} -1 =\]
- \[ = \frac{1}{ M-1}\cdot \left [1- 2 \cdot M \cdot {\rm Q} \left( \sqrt{2\pi} \cdot {\rm ld}\hspace{0.1cm}(M) \cdot {f_{\rm G}}/{R_{\rm B}} \right)\right] \hspace{0.05cm}.\]
Man erkennt aus obiger Grafik:
- Bei breitbandigem Filter (das heißt: für großes fG) ist das Binärsystem den Mehrstufensystemen deutlich überlegen. Die normierte halbe Augenöffnung beträgt im Grenzfall önorm = 1 (für M = 2), önorm = 1/2 (für M = 3) bzw. önorm = 1/3 (für M = 4).
- Wie aus obiger Grafik hervorgeht, führt für Grenzfrequenzen fG/RB < 0.35 die Stufenzahl M = 4 (rote Kurve) zu einer größeren Augenöffnung als M = 2 (blaue Kurve). Das Ternärsystem (M = 3, violette Kurve) liegt fast im gesamten Bereich zwischen dem Binär– und dem Quaternärsystem.
- Besonders erwähnenswert ist, dass sich beim Quaternärsystem erst mit einer Grenzfrequenz <nobr>fG/RB < 0.23</nobr> ein geschlossenes Auge ergibt (was zu sehr großen Fehlerwahrscheinlichkeiten führt), während die Binärübertragung bereits für fG/RB < 0.27 nicht mehr möglich ist.
Vergleich zwischen Binär– und Quaternärsystem (2)
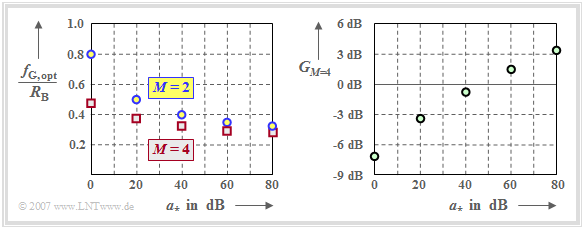
Vergleichen wir nun die optimalen Grenzfrequenzen des Gaußfilters, die sich für M = 2 bzw. M = 4 ergeben. Dem Vergleich liegt ein koaxialer Übertragungskanal mit der charakteristischen Kabeldämpfung a∗ zugrunde. Je größer dieser Kanalparameter ist (das heißt auch: wie größer die Kabellänge ist), desto stärker wird das Rauschen durch die erforderliche Entzerrung beim Empfänger verstärkt.
Interpretieren wir zunächst die linke Grafik:
- Bei verzerrungsfreiem Kanal (a∗ = 0 dB) ergeben sich die optimalen Grenzfrequenzen zu 0.8 (für M = 2) bzw. 0.48 (für M = 4) – jeweils normiert auf die äquivalente Bitrate. Entsprechend dem Kurvenverlauf ö(TD)/(2s0) auf der letzten Seite ist hier das Binärsystem dem Quaternärsystem deutlich überlegen.
- Mit der charakteristischen Kabeldämpfung a∗ = 80 dB erhält man für das Binärsystem (M = 2) die optimale Grenzfrequenz fG,opt = 0.33/T. Für das Quaternärsystem (für M = 4) ergibt sich ein kleinerer Wert: fG,opt = 0.28/T.
Das optimierte Binärsystem ist aber trotz größerer Augenöffnung nicht immer besser als das optimierte Quaternärsystem, da auch die Rauschleistung zu berücksichtigen ist. Diese wird mit kleiner werdenden Grenzfrequenz ebenfalls kleiner.
Die rechte Grafik zeigt den Störabstandsgewinn des Quaternärsystems gegenüber dem Binärsystem,
\[G_{_{M=4}} = 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{_{{\rm U},\hspace{0.05cm} M=4}} - 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{_{{\rm U}, \hspace{0.05cm}M=2}},\]
wenn die Grenzfrequenzen gemäß der linken Grafik jeweils optimal gewählt werden. Demnach gilt:
- Für a∗ < 50 dB ist das Binärsystem optimal. Beim verzerrungsfreien Kanal (a∗ = 0 dB) ergibt sich ein um ca. 7 dB größeres SNR als mit M = 4.
- Dagegen ergeben sich für a∗ ≥ 50 dB günstigere Verhältnisse für die Quaternärübertragung. Bei 80 dB Kabeldämpfung ist der Störabstandsgewinn gegenüber M = 2 größer als 3 dB.
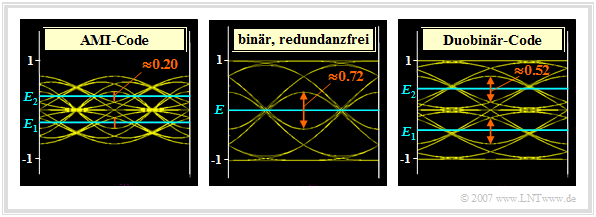
Augenöffnung bei den Pseudoternärcodes (1)
In Kapitel 2.4 wurden die Pseudoternärcodes allgemein beschrieben und es wurden für diese die Augendiagramme bei Nyquistimpulsformung angegeben. In der Grafik auf dieser Seite sehen Sie die Augendiagramme – jeweils ohne Rauschen – für den AMI–Code (links) und den Duobinärcode (rechts) im Vergleich zum redundanzfreien Binärcode (Mitte). Die Amplitude ist jeweils zu s0 = 1 normiert.
Alle Augendiagramme gelten für ein gaußförmiges Empfangsfilter mit der Grenzfrequenz fG · T = 0.4, woraus sich folgende (normierte) Grundimpulswerte ergeben:
\[g_{0} \approx 0.68, \hspace{0.2cm} g_{1}= g_{-1} \approx 0.16, \hspace{0.2cm}\hspace{0.2cm} g_{2}= g_{-2}= ... \approx 0 \hspace{0.05cm}.\]
Beim redundanzfreien Binärsystem (mittlere Grafik) erhält man somit für die Augenöffnung
\[{\ddot{o}(T_{\rm D})}= 2 \cdot (g_0 - 2 \cdot g_1 ) = 0.72 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \ddot{o}_{\rm norm} = \frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = 0.36\]
im Vergleich zu ö(TD) = 2 bzw. önorm = 1 beim binären Nyquistsystem.
Da die Pseudoternärcodes mit der gleichen Symbolrate arbeiten wie das redundanzfreie Binärsystem,
- sind die Detektionsgrundimpulswerte gν und auch der Rauscheffektivwert σd in allen Fällen gleich,
- ist die (halbe) Augenöffnung für die Systemoptimierung ebenso geeignet wie das S/N–Verhältnis ρU = [ö(TD)/2]2/σd2 und die daraus resultierende (ungünstigste) Fehlerwahrscheinlichkeit pU.
Die Beschreibung der beiden äußeren Augendiagramme folgt auf der nächsten Seite.