Aufgaben:Aufgabe 2.4: Frequenz– und Phasenversatz: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 31: | Zeile 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welche der nachfolgenden Aussagen sind zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Der Demodulator würde bei ZSB–AM mit Träger besser arbeiten. |
| − | + | + | + Der Träger würde die Sendeleistung unnötigerweise vergrößern. |
| + | + Die richtige Dimensionierung des Tiefpasses $H_E(f)$ ist essentiell. | ||
| + | - Man könnte auch einen Hüllkurvendemodulator verwenden. | ||
| + | + Hüllkurvendemodulation ist nur für m < 1 anwendbar. | ||
| − | { | + | |
| + | {Wie sind die Signalparameter von $z_E(t)$ zu wählen, damit $υ(t) = q(t)$ gilt? | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_E$ = { 2 3% } |
| + | $f_F$ = { 50 3% } $\text{KHz}$ | ||
| + | $\phi_E$ { -90 } | ||
| + | {Es gelte $f_E = f_T$. Welches Sinkensignal $υ(t)$ ergibt sich mit $ϕ_E = – 120°$? Geben Sie dessen Signalwert bei t = 0 ein. | ||
| + | |type="{}"} | ||
| + | $ϕ_E = –120°: υ(t = 0)$ = { 1.732 3% } $\text{V}$ | ||
| + | {Es gelte $f_E = f_T$. Welches Sinkensignal $υ(t)$ ergibt sich mit $ϕ_E = 0$? Geben Sie den Signalwert bei t = 0 ein. | ||
| + | |type="{}"} | ||
| + | $ϕ_E = 0: υ(t = 0)$ = { 0 3% } $\text{V}$ | ||
| + | |||
| + | |||
| + | {Es gelte $ϕ_E = ϕ_T$. Welches Sinkensignal erhält man mit $Δf_T = f_E – f_T = 1 kHz$? Welche der nachfolgenden Aussagen sind richtig? | ||
| + | |type="[]"} | ||
| + | + gilt $υ(t) = q(t) · cos(2π · Δf_T · t).$ | ||
| + | - $υ(t)$ beinhaltet einen Spektralanteil bei 2 kHz. | ||
| + | + $υ(t)$ beinhaltet einen Spektralanteil bei 4 kHz. | ||
| + | + $υ(t)$ beinhaltet einen Spektralanteil bei 6 kHz. | ||
</quiz> | </quiz> | ||
Version vom 30. Dezember 2016, 17:37 Uhr
Betrachtet wird das Quellensignal $$q(t) = A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) +A_{\rm 2} \cdot \sin(2 \pi f_{\rm 2} t )$$ mit den Signalparametern $$ A_1 = 2\,{\rm V}, \hspace{0.15cm}f_1 = 2\,{\rm kHz}, \hspace{0.15cm}$$ $$A_2 = 1\,{\rm V}, \hspace{0.15cm}f_2 = 5\,{\rm kHz}\hspace{0.05cm}.$$ Dieses Signal wird ZSB–amplitudenmoduliert.
Das modulierte Signal $s(t)$ besitzt somit Spektralanteile bei $±45 kHz$, $±48 kHz$, $±52 kHz$ und $±55 kHz$. Bekannt ist weiter, dass das sendeseitige Trägersignal einen sinusförmigen Verlauf hat ($ϕ_T = –90°$).
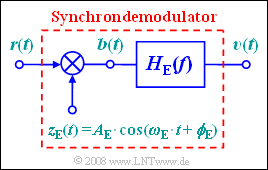
Die Demodulation soll mit nebenstehend skizzierter Schaltung erfolgen, die durch folgende Parameter bestimmt ist:
- Amplitude $A_E$ (ohne Einheit),
- Frequenz $f_E$,
- Phase $ϕ_E$.
Der Block $H_E(f)$ beschreibt einen idealen, rechteckförmigen Tiefpass, der geeignet dimensioniert ist.
Hinweis: Diese Aufgabe gehört zum Themengebiet von Kapitel 2.2. Berücksichtigen Sie die folgenden trigonometrischen Umformungen:
$$\\cos(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) + \cos(\alpha+\beta)\right] \hspace{0.05cm},$$
$$\\sin(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \sin(\alpha-\beta) + \sin(\alpha+\beta)\right] \hspace{0.05cm},$$
$$\\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right] \hspace{0.05cm}.$$
Fragebogen
Musterlösung