Aufgaben:Aufgabe 3.1Z: Einfluss der Nachrichtenphase bei PM: Unterschied zwischen den Versionen

Version vom 2. Januar 2017, 15:42 Uhr

Wir betrachten die Phasenmodulation verschiedener Schwingungen $$ q(t) = \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}.$$ Das Quellensignal ist hierbei normiert (Amplitude 1) dargestellt, so dass das phasenmodulierte Signal mit dem Modulationsindex (bzw. Phasenhub) $η$ wie folgt beschrieben werden kann: $$s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T} \cdot t + \eta \cdot q(t) \right)\hspace{0.05cm}.$$ Das in der oberen Grafik dargestellte Signal $s_1(t)$ ist durch die Parameterwerte $ϕ_N = –90°$ und $η_1 = 2$ charakterisiert. Die Frequenz $f_N$ dieses sinusförmigen Quellensignals soll ebenso wie die Trägerfrequenz $f_T$ aus dem dargestellten Signalausschnitt der Dauer $200 μs$ ermittelt werden.

Das Signal $s_2(t)$ unterscheidet sich von $s_1(t)$ möglicherweise durch eine andere Nachrichtenphase $ϕ_N$ und einen anderen Modulationsindex $η$. Alle anderen Systemparameter sind gegenüber $s_1(t)$ unverändert.

Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 3.1.

Fragebogen

Musterlösung

1. Man erkennt aus der Skizze, dass der dargestellte Signalausschnitt der Dauer $200 μs$ genau der Periodendauer des sinusförmigen Quellensignals entspricht. Daraus folgt $f_N = 5 kHz$. Zu den Zeitpunkten $t = 0$, $t = 100 μs$ und $t = 200 μs$ sind die Signale $z(t)$ und $s(t)$ phasensynchron. In der ersten Halbwelle von $q(t)$ kommen die Nulldurchgänge von $s(t)$ etwas früher als die des Trägersignals $z(t)$, was auf eine positive Phase hinweist. Dagegen ist im Bereich von 100 bis 200 μs die Phase $ϕ(t) < 0$.

2. Es gilt $f_T = 50 kHz$, da im dargestellten Signalausschnitt ($200 μs$) von $z(t)$ genau 10 Perioden abgezählt werden können.

3. Die maximale relative Phasenabweichung beträgt $ϕ_{max} = η_1/(2π) ≈ 0.318$.

4.Da die Periodendauer des Trägers $T_0 = 20 μs$ ist, erhält man $Δt_{max} = ϕ_{max} ·T0 ≈ 6.37 μs$.

5. Die maximale Phasenabweichung (Verschiebung der Nulldurchgänge) ist bei $s_2(t)$ genau so groß wie bei $s_1(t)$. Daraus kann auf $η_2 = η_1 = 2$ geschlossen werden.

6.Das Signal $s_2(t)$ ist gegenüber $s_1(t)$ um $25 μs$ nach rechts verschoben. Deshalb muss auch für die Quellensignale gelten: $$ q_2(t) = q_1(t - 25\,{\rm \mu s}) = \cos(2 \pi f_{\rm N} (t - 25\,{\rm \mu s}) ) = \cos (\omega_{\rm N} \cdot t - 0.75 \cdot \pi)\hspace{0.05cm}.$$ Dies entspricht der Phasenlage $ϕ_{N2} = –135°$.

@@ Zeile 3: / Zeile 3: @@
 }}
-[[Datei:|right|]]
+[[Datei:P_ID1080__Mod_Z_3_1.png|right|]]
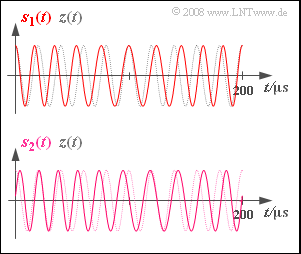
+Wir betrachten die Phasenmodulation verschiedener Schwingungen
+$$ q(t) = \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}.$$
+Das Quellensignal ist hierbei normiert (Amplitude 1) dargestellt, so dass das phasenmodulierte Signal mit dem Modulationsindex (bzw. Phasenhub) $η$ wie folgt beschrieben werden kann:
+$$s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T} \cdot t + \eta \cdot q(t) \right)\hspace{0.05cm}.$$
+Das in der oberen Grafik dargestellte Signal $s_1(t)$ ist durch die Parameterwerte $ϕ_N = –90°$ und $η_1 = 2$ charakterisiert. Die Frequenz $f_N$ dieses sinusförmigen Quellensignals soll ebenso wie die Trägerfrequenz $f_T$ aus dem dargestellten Signalausschnitt der Dauer $200 μs$ ermittelt werden.
+Das Signal $s_2(t)$ unterscheidet sich von $s_1(t)$ möglicherweise durch eine andere Nachrichtenphase $ϕ_N$ und einen anderen Modulationsindex $η$. Alle anderen Systemparameter sind gegenüber $s_1(t)$ unverändert.
+'''Hinweis:''' Die Aufgabe bezieht sich auf die theoretischen Grundlagen von [http://www.lntwww.de/Modulationsverfahren/Phasenmodulation_(PM) Kapitel 3.1].
@@ Zeile 9: / Zeile 18: @@
 <quiz display=simple>
-{Multiple-Choice Frage
-|type="[]"}
-- Falsch
-+ Richtig
+{Ermitteln Sie die Frequenz des Nachrichtensignals.
+|type="{}"}
+$f_N$ = { 5 3%  } $KHz$
+{Wie groß ist die Trägerfrequenz?
+|type="{}"}
+$f_T$ = { 50 3% } $KHz$
+{Wie groß ist die maximale Phasenabweichung zwischen $z(t)$ und $s(t)$?
+|type="{}"}
+$ϕ_{max}$ = { 0.318 3% } $rad$
+{Zu welcher Zeitverschiebung der Nulldurchgänge führt diese Phase?
+|type="{}"}
+$Δt_{max}$ = { 6.37 3% } $μs$
-{Input-Box Frage
+{Bestimmen Sie den Modulationsindex $η_2$ für das Signal $s_2(t).
 |type="{}"}
-$\alpha$ = { 0.3 }
+$η_2$ = { 2 3% }
+{Welche Phasenlage hat das für $s_2(t)$ zugrunde liegende Quellensignal?
+|type="{}"}
+$ϕ_{N2}$ = { -135 3% } $Grad$
@@ Zeile 25: / Zeile 48: @@
 ===Musterlösung===
 {{ML-Kopf}}
-'''1.'''
+'''1.''' Man erkennt aus der Skizze, dass der dargestellte Signalausschnitt der Dauer $200 μs$ genau der Periodendauer des sinusförmigen Quellensignals entspricht. Daraus folgt $f_N = 5 kHz$. Zu den Zeitpunkten $t = 0$, $t = 100 μs$ und $t = 200 μs$ sind die Signale $z(t)$ und $s(t)$ phasensynchron. In der ersten Halbwelle von $q(t)$ kommen die Nulldurchgänge von $s(t)$ etwas früher als die des Trägersignals $z(t)$, was auf eine positive Phase hinweist. Dagegen ist im Bereich von 100 bis 200 μs die Phase $ϕ(t) < 0$.
-'''2.'''
-'''3.'''
-'''4.'''
+'''2.''' Es gilt $f_T = 50 kHz$, da im dargestellten Signalausschnitt ($200 μs$) von $z(t)$ genau 10 Perioden abgezählt werden können.
-'''5.'''
-'''6.'''
+'''3.'''  Die maximale relative Phasenabweichung beträgt $ϕ_{max} = η_1/(2π) ≈ 0.318$.
-'''7.'''
+'''4.'''Da die Periodendauer des Trägers $T_0 = 20 μs$ ist, erhält man $Δt_{max} = ϕ_{max} ·T0 ≈ 6.37 μs$.
+'''5.''' Die maximale Phasenabweichung (Verschiebung der Nulldurchgänge) ist bei $s_2(t)$ genau so groß wie bei $s_1(t)$. Daraus kann auf $η_2 = η_1 = 2$ geschlossen werden.
+'''6.'''Das Signal $s_2(t)$ ist gegenüber $s_1(t)$ um $25 μs$ nach rechts verschoben. Deshalb muss auch für die Quellensignale gelten:
+$$ q_2(t) = q_1(t - 25\,{\rm \mu s}) = \cos(2 \pi f_{\rm N} (t - 25\,{\rm \mu s}) ) = \cos (\omega_{\rm N} \cdot t - 0.75 \cdot \pi)\hspace{0.05cm}.$$
+Dies entspricht der Phasenlage $ϕ_{N2} = –135°$.
 {{ML-Fuß}}