Digitalsignalübertragung/Bündelfehlerkanäle: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{Header |Untermenü=Digitale Kanalmodelle |Vorherige Seite=Binary Symmetric Channel (BSC) |Nächste Seite=Anwendungen bei Multimedia–Dateien }} == Kanalm…“) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 77: | Zeile 77: | ||
Zu jedem Taktzeitpunkt wird genau ein Element der Fehlerfolge 〈<i>e<sub>ν</sub></i>〉 entsprechend der aktuellen Fehlerwahrscheinlichkeit (<i>p</i><sub>G</sub> bzw. <i>p</i><sub>B</sub>) erzeugt. Die Simulation des Fehlerabstandes ist hier nicht anwendbar, da ein Zustandswechsel nach jedem Symbol (und nicht nur nach einem Fehler) möglich ist.<br> | Zu jedem Taktzeitpunkt wird genau ein Element der Fehlerfolge 〈<i>e<sub>ν</sub></i>〉 entsprechend der aktuellen Fehlerwahrscheinlichkeit (<i>p</i><sub>G</sub> bzw. <i>p</i><sub>B</sub>) erzeugt. Die Simulation des Fehlerabstandes ist hier nicht anwendbar, da ein Zustandswechsel nach jedem Symbol (und nicht nur nach einem Fehler) möglich ist.<br> | ||
| + | |||
| + | == Fehlerabstandsverteilung des GE–Modells == | ||
| + | <br> | ||
| + | In Huber, J.: <i>Codierung für gedächtnisbehaftete Kanäle.</i> Dissertation – Universität der Bundeswehr München, 1982 finden sich die analytischen Berechnungen | ||
| + | *der Wahrscheinlichkeit des Fehlerabstandes <i>k</i>: | ||
| + | |||
| + | ::<math>{\rm Pr}(a=k) = \alpha_{\rm G} \cdot \beta_{\rm | ||
| + | G}^{\hspace{0.05cm}k-1} \cdot (1- \beta_{\rm G}) + \alpha_{\rm B} | ||
| + | \cdot \beta_{\rm B}^{\hspace{0.05cm}k-1} \cdot (1- \beta_{\rm | ||
| + | B})\hspace{0.05cm},</math> | ||
| + | |||
| + | *der Fehlerabstandsverteilung: | ||
| + | |||
| + | ::<math>V_a(k) = {\rm Pr}(a \ge k) = \alpha_{\rm G} \cdot \beta_{\rm | ||
| + | G}^{\hspace{0.05cm}k-1} | ||
| + | + \alpha_{\rm B} \cdot \beta_{\rm | ||
| + | B}^{\hspace{0.05cm}k-1} \hspace{0.05cm}.</math> | ||
| + | |||
| + | Hierbei sind folgende Hilfsgrößen verwendet: | ||
| + | |||
| + | :<math>u_{\rm GG} \hspace{-0.1cm} = \hspace{-0.1cm}{\rm Pr}(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) | ||
| + | \hspace{0.05cm},\hspace{0.2cm} | ||
| + | {\it u}_{\rm GB} ={\rm Pr}(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\hspace{0.03cm} \rm G}) | ||
| + | \hspace{0.05cm},</math> | ||
| + | :<math>u_{\rm BB} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr}(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B}) | ||
| + | \hspace{0.05cm},\hspace{0.29cm} | ||
| + | {\it u}_{\rm BG} ={\rm Pr}(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm | ||
| + | B})\hspace{0.05cm}</math> | ||
| + | |||
| + | :<math>\Rightarrow \hspace{0.3cm} \beta_{\rm G} \hspace{-0.1cm} = | ||
| + | \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - | ||
| + | u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} | ||
| + | \hspace{0.05cm},</math> | ||
| + | :<math>\hspace{0.8cm}\beta_{\rm B} \hspace{-0.1cm} = \hspace{-0.1cm}\frac{u_{\rm | ||
| + | GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot | ||
| + | u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}.</math> | ||
| + | |||
| + | :<math>x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} | ||
| + | \hspace{0.05cm},\hspace{0.2cm} | ||
| + | x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}</math> | ||
| + | |||
| + | :<math>\Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot | ||
| + | p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm | ||
| + | B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, | ||
| + | \hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.</math> | ||
| + | |||
| + | Die angegebenen Gleichungen sind das Ergebnis umfangreicher Matrizenoperationen.<br> | ||
| + | |||
| + | [[Datei:P ID1838 Dig T 5 3 S2 version1.png|Fehlerabstandsverteilung von GE– und BSC–Modell|class=fit]]<br> | ||
| + | |||
| + | *Die Abbildung zeigt die Fehlerabstandsverteilung (FAV) des GE–Modells (rote Kurve) in linearer und logarithmischer Darstellung für Pr(G|B) = 0.1, Pr(B|G) = 0.01, <i>p</i><sub>G</sub> = 0.001 und <i>p</i><sub>B</sub> = 0.4.<br> | ||
| + | |||
| + | *Zum Vergleich ist auch der Verlauf von <i>V<sub>a</sub></i>(<i>k</i>) für das BSC–Modell mit der gleichen mittleren Fehlerwahrscheinlichkeit <i>p</i><sub>M</sub> = 4.5% als blaue Kurve eingezeichnet.<br> | ||
| + | |||
| + | |||
| + | |||
| + | |||
{{Display}} | {{Display}} | ||
Version vom 2. Januar 2017, 23:57 Uhr
Kanalmodell nach Gilbert–Elliott (1)
Dieses auf E. N. Gilbert Gilbert, E. N.: Capacity of Burst–Noise Channel. In: Bell Syst. Techn. J. Vol. 39, 1960, pp. 1253–1266 und E. O. Elliott Elliott, E.O.: Estimates of Error Rates for Codes on Burst–Noise Channels. In: Bell Syst. Techn. J., Vol. 42, (1963), pp. 1253 – 1266 zurückgehende Kanalmodell eignet sich zur Beschreibung und Simulation von digitalen Übertragungssystemen mit Bündelfehlercharakteristik.
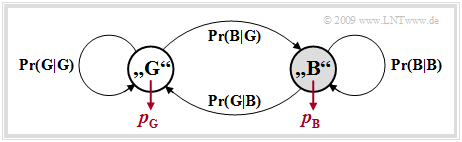
Das Gilbert–Elliott–Modell (Kurzbezeichnung: GE–Modell) lässt sich wie folgt charakterisieren:
- Die unterschiedliche Übertragungsqualität zu unterschiedlichen Zeiten wird durch eine endliche Anzahl g von Kanalzuständen (Z1, Z2, ..., Zg) ausgedrückt.
- Die in Wirklichkeit fließenden Übergänge der Störintensität – im Extremfall von völlig fehlerfreier Übertragung bis hin zum Totalausfall – werden beim GE–Modell durch feste Wahrscheinlichkeiten in den einzelnen Kanalzuständen approximiert.
- Die Übergänge zwischen den g Zuständen erfolgen gemäß einem Markovprozess (1. Ordnung) und werden durch g · (g – 1) Übergangswahrscheinlichkeiten gekennzeichnet. Zusammen mit den g Fehlerwahrscheinlichkeiten in den einzelnen Zuständen gibt es somit g2 freie Modellparameter.
- Aus Gründen der mathematischen Handhabbarkeit beschränkt man sich meist auf g = 2 Zustände und bezeichnet diese mit „G” (GOOD) und „B” (BAD). Meist wird die Fehlerwahrscheinlichkeit im Zustand „G” sehr viel kleiner sein als im Zustand „B”.
- Im Folgenden benutzen wir diese beiden Fehlerwahrscheinlichkeiten pG und pB, wobei pG < pB gelten soll, sowie die Übergangswahrscheinlichkeiten Pr(B|G) und Pr(G|B). Damit sind auch die beiden anderen Übergangswahrscheinlichkeiten festgelegt:
- \[{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) = 1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G), \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B) = 1 - {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{0.05cm}.\]
Kanalmodell nach Gilbert–Elliott (2)
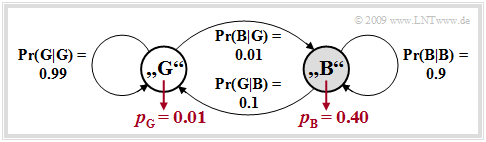
Beispielhaft betrachten wir nun das GE–Modell mit den Parametern
\[p_{\rm G} = 0.01, \hspace{0.2cm}p_{\rm B} = 0.4, \hspace{0.2cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) = 0.1, \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.\]
Die nachfolgende Grafik zeigt eine dazugehörige (mögliche) Fehlerfolge der Länge N = 800.
Befindet sich das GE–Modell im Zustand „BAD”, so erkennt man dies an der grauen Hinterlegung. Die Wahrscheinlichkeiten, dass sich die Markovkette im Zustand „G” bzw. „B” befindet, lassen sich aus der vorausgesetzten Homogenität und Stationarität berechnen. Man erhält mit den obigen Zahlenwerten:
\[w_{\rm G} \hspace{-0.15cm} = \hspace{-0.15cm} {\rm Pr(im\hspace{0.15cm} Zustand \hspace{0.15cm}G)}= \frac{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = \frac{0.1}{0.1 + 0.01} = {10}/{11}\hspace{0.05cm},\] \[w_{\rm B} \hspace{-0.15cm} = \hspace{-0.15cm} {\rm Pr(im\hspace{0.15cm} Zustand \hspace{0.15cm}B)}= \frac{{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = \frac{0.11}{0.1 + 0.01} = {1}/{11}\hspace{0.05cm}.\]
Damit kann auch die mittlere Fehlerwahrscheinlichkeit des GE–Modells ermittelt werden:
\[p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} = \frac{p_{\rm G} \cdot {\rm Pr}({\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}+ p_{\rm B} \cdot {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} \hspace{0.05cm}.\]
Insbesondere gilt für das hier beispielhaft betrachtete Modell:
\[p_{\rm M} ={10}/{11} \cdot 0.01 +{1}/{11} \cdot 0.4 = {1}/{22} \approx 4.55\%\hspace{0.05cm}.\]
Zur Simulation einer GE–Fehlerfolge wird zwischen den Zuständen „G” und „B” entsprechend den vier Übergangswahrscheinlichkeiten umgeschaltet. Beim ersten Aufruf erfolgt die Auswahl des Zustandes zweckmäßigerweise entsprechend den Wahrscheinlichkeiten wG und wB.
Zu jedem Taktzeitpunkt wird genau ein Element der Fehlerfolge 〈eν〉 entsprechend der aktuellen Fehlerwahrscheinlichkeit (pG bzw. pB) erzeugt. Die Simulation des Fehlerabstandes ist hier nicht anwendbar, da ein Zustandswechsel nach jedem Symbol (und nicht nur nach einem Fehler) möglich ist.
Fehlerabstandsverteilung des GE–Modells
In Huber, J.: Codierung für gedächtnisbehaftete Kanäle. Dissertation – Universität der Bundeswehr München, 1982 finden sich die analytischen Berechnungen
- der Wahrscheinlichkeit des Fehlerabstandes k:
- \[{\rm Pr}(a=k) = \alpha_{\rm G} \cdot \beta_{\rm G}^{\hspace{0.05cm}k-1} \cdot (1- \beta_{\rm G}) + \alpha_{\rm B} \cdot \beta_{\rm B}^{\hspace{0.05cm}k-1} \cdot (1- \beta_{\rm B})\hspace{0.05cm},\]
- der Fehlerabstandsverteilung:
- \[V_a(k) = {\rm Pr}(a \ge k) = \alpha_{\rm G} \cdot \beta_{\rm G}^{\hspace{0.05cm}k-1} + \alpha_{\rm B} \cdot \beta_{\rm B}^{\hspace{0.05cm}k-1} \hspace{0.05cm}.\]
Hierbei sind folgende Hilfsgrößen verwendet:
\[u_{\rm GG} \hspace{-0.1cm} = \hspace{-0.1cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) \hspace{0.05cm},\hspace{0.2cm} {\it u}_{\rm GB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\hspace{0.03cm} \rm G}) \hspace{0.05cm},\] \[u_{\rm BB} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B}) \hspace{0.05cm},\hspace{0.29cm} {\it u}_{\rm BG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B})\hspace{0.05cm}\]
\[\Rightarrow \hspace{0.3cm} \beta_{\rm G} \hspace{-0.1cm} = \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} \hspace{0.05cm},\] \[\hspace{0.8cm}\beta_{\rm B} \hspace{-0.1cm} = \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}.\]
\[x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} \hspace{0.05cm},\hspace{0.2cm} x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}\]
\[\Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, \hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.\]
Die angegebenen Gleichungen sind das Ergebnis umfangreicher Matrizenoperationen.
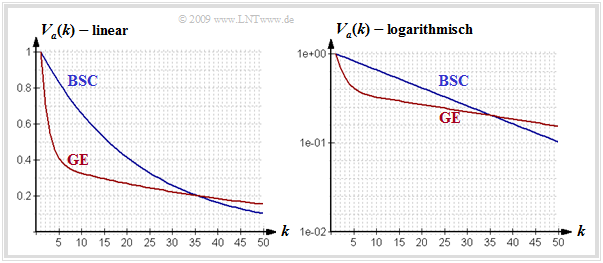
- Die Abbildung zeigt die Fehlerabstandsverteilung (FAV) des GE–Modells (rote Kurve) in linearer und logarithmischer Darstellung für Pr(G|B) = 0.1, Pr(B|G) = 0.01, pG = 0.001 und pB = 0.4.
- Zum Vergleich ist auch der Verlauf von Va(k) für das BSC–Modell mit der gleichen mittleren Fehlerwahrscheinlichkeit pM = 4.5% als blaue Kurve eingezeichnet.