Aufgaben:Aufgabe 3.9: Kreisbogen und Parabel

• Zurück zum Buch

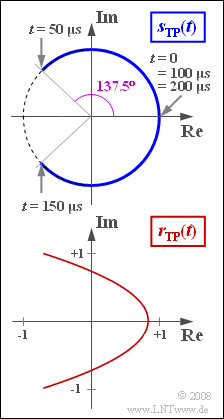
Wir betrachten hier die Frequenzmodulation eines cosinusförmigen Quellensignals $$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t )$$ mit der Amplitude $A_N = 1 V$ und der Frequenz $f_N = 5 kHz$. Der Modulationsindex (Phasenhub) beträgt $η = 2.4$. Das zugehörige TP–Signal lautet bei normierter Trägeramplitude ($A_T = 1$): $$ s_{\rm TP}(t) = \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}.$$ Dieses beschreibt einen Kreisbogen. Innerhalb der Periodendauer $T_N = 1/f_N = 200 μs$ ergeben sich folgende Phasenwinkel: $$: \phi(0) = 0, \hspace{0.2cm}\phi(0.25 \cdot T_{\rm N}) = \eta, \hspace{0.2cm}\phi(0.5 \cdot T_{\rm N})= 0,$$ $$ \phi(0.75 \cdot T_{\rm N})= -\eta,\hspace{0.2cm}\phi(T_{\rm N})= 0.$$ Die erforderliche Kanalbandbreite zur Übertragung dieses Signals ist theoretisch unendlich groß. Ist die Bandbreite jedoch begrenzt, z. B. auf $B_K = 25 kHz$, so kann das äquivalente TP–Signal des Empfangssignals wie folgt beschrieben werden: $$r_{\rm TP}(t) = \sum_{n = - 2}^{+2}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}.$$ In diesem Fall ergibt sich eine parabelförmige Ortskurve $$ y^2 + a \cdot x + b = 0,$$ die in dieser Aufgabe analysiert werden soll.

Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 3.1 und Kapitel 3.2. Gehen Sie bei der Berechnung von folgenden Werten der Besselfunktion aus: $${\rm J}_0 (2.4) \approx 0, \hspace{0.2cm}{\rm J}_1 (2.4) = -{\rm J}_{-1} (2.4)\approx 0.52, \hspace{0.2cm}{\rm J}_2 (2.4) = {\rm J}_{-2} (2.4)\approx 0.43.$$

Fragebogen

1

Wie groß ist die Modulatorkonstante?

$K_FM$ = $(Vs)^{-1}$

2

Berechnen Sie den Realteil $x(t) = Re[r_{TP}(t)]$ des äquivalenten TP-Signals und geben Sie dessen Maximum und Minimum an.

$x_{max}$ =

$x_{min}$ =

3

Wie groß ist das Maximum und Minimum des Imaginärteils $y(t) = Im[r_TP(t)]$?

$y_{max}$ =

$y_{min}$ =

4

Welche asenwerte ergeben sich bei allen Vielfachen von $T_N/2$?

$ϕ(t = n · T_N/2)$ = $Grad$

5

Wie groß ist der maximale Phasenwinkel $ϕ_{max}$? Interpretieren Sie das Ergebnis.

$ϕ_{max}$ = $Grad$

6

Zeigen Sie, dass man die Ortskurve in der Form $y^² + a · x + b = 0$ angeben kann. Bestimmen Sie die Parabelparameter a und b.

$a$ =

$b$ =

Musterlösung

Musterlösung

1. Bei Frequenzmodulation eines Cosinussignals gilt für den Modulationsindex: $$ \eta = \frac{K_{\rm FM} \cdot A_{\rm N}}{ \omega_{\rm N}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K_{\rm FM} = \frac{2 \pi \cdot f_{\rm N }\cdot \eta}{ A_{\rm N}}=$$ $$= \frac{2 \pi \cdot 5 \cdot 10^3 \,{\rm Hz}\cdot 2.4}{ 1\,{\rm V}} \hspace{0.15cm}\underline {\approx 7.54 }\cdot 10^4 \,\,{\rm V}^{-1}{\rm s}^{-1}\hspace{0.05cm}.$$ 2. Die angegebene Gleichung für das äquivalente TP–Signal lautet in ausgeschriebener Form mit der Abkürzung $γ = ω_N · t$ unter Berücksichtigung von $J_{–1} = –J_1$ und $J_{–2} = J_2$: $$r_{\rm TP}(t) = {\rm J}_0 + \left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \gamma} - {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \gamma} \right]\cdot {\rm J}_1 \hspace{0.27cm} +\left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\gamma} + {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\gamma} \right]\cdot {\rm J}_2 =$$ $$ = {\rm J}_0 + 2 \cdot {\rm j} \cdot {\rm J}_1 \cdot \sin (\gamma)+ 2 \cdot {\rm J}_2 \cdot \cos (2\gamma)\hspace{0.05cm} .$$ Somit ergibt sich für den Realteil allgemein bzw. für $η = 2.4$, das heißt $J_0 = 0$, $J_2 = 0.43$: $$ x(t) = {\rm J}_0 + 2 \cdot {\rm J}_2 \cdot \cos (2 \omega_{\rm N} t ) = 2 \cdot {\rm J}_2 \cdot \cos (2 \omega_{\rm N} t ) \hspace{0.05cm}$$ $$\Rightarrow \hspace{0.3cm} x_{\rm max} = 2 \cdot {\rm J}_2\hspace{0.15cm}\underline { = 0.86}, \hspace{0.3cm} x_{\rm min} = -x_{\rm max} \hspace{0.15cm}\underline {= -0.86}\hspace{0.05cm}.$$ 3. Entsprechend dem Ergebnis aus b) erhält man für den Imaginärteil ($J_1 = 0.52$): $$y(t) = 2 \cdot {\rm J}_1 \cdot \sin ( \omega_{\rm N} t )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} y_{\rm max} =2 \cdot {\rm J}_1\hspace{0.15cm}\underline { = 1.04}\hspace{0.05cm}, \hspace{0.3cm} y_{\rm min} = -y_{\rm max}\hspace{0.15cm}\underline { = -1.04}\hspace{0.05cm}.$$

4. Der Imaginärteil ist zu diesen Zeitpunkten jeweils 0 und damit auch die Phasenfunktion. Diesen Sachverhalt erkennt man auch aus der Skizze auf der Angabenseite.

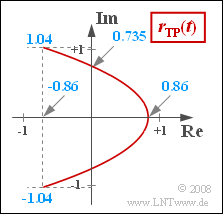
5. Aus der Skizze ist bereits zu erkennen, dass der Phasenwinkel beispielsweise für $t = T_N/4$ seinen Maximalwert erreicht. Dieser kann mit $y_{max} = 1.04$ und $x_{min} = –0.86$ wie folgt berechnet werden: $$\phi_{\rm max} = \arctan \frac{y_{\rm max}}{x_{\rm min}} = \arctan (-1.21) = 180^\circ - 50.4^\circ \hspace{0.15cm}\underline {= 129.6^\circ} \hspace{0.05cm}.$$ Ohne Bandbegrenzung würde sich hier der Phasenwinkel $ϕ(t = T_N/4) = η = 2.4 = 137.5°$ ergeben. Die maximale Abweichung des Sinkensignals vom Quellensignal tritt somit z.B. zur Zeit $t = T_N/4$ auf.

6. Mit $γ = ω_N · t$ und $cos(2γ) = 1 – 2 · cos^2(γ)$ kann für Real– und Imaginärteil geschrieben werden: $$x = {\rm J}_0 + 4 \cdot {\rm J}_2 \cdot \cos^2 (\gamma) - 2 \cdot {\rm J}_2\hspace{0.05cm},\hspace{0.3cm} y = 2 \cdot {\rm J}_1 \cdot \sin (\gamma) \hspace{0.05cm}.$$ Diese Gleichungen können wie folgt umgeformt werden: $$\cos^2 (\gamma) =\frac{x-{\rm J}_0 + 2 \cdot {\rm J}_2 }{4 \cdot {\rm J}_2} \hspace{0.05cm},\hspace{0.3cm} \sin^2 (\gamma) = \frac{y^2 }{4 \cdot {\rm J}_1^2}$$ $$\Rightarrow \hspace{0.3cm} \frac{y^2 }{4 \cdot {\rm J}_1^2} + \frac{x-{\rm J}_0 + 2 \cdot {\rm J}_2 }{4 \cdot {\rm J}_2} =1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {y^2 } + \frac{{\rm J}_1^2}{ {\rm J}_2} \cdot x + {{\rm J}_1^2} \cdot \left ( 2 - \frac{{\rm J}_0}{ {\rm J}_2} \right ) =0\hspace{0.05cm}.$$

Damit lauten die Parabelparameter für $J_0 = 0$: $$a = \frac{{\rm J}_1^2}{ {\rm J}_2} \hspace{0.15cm}\underline {\approx 0.629}, \hspace{0.3cm} b = 2 \cdot {\rm J}_1^2 \hspace{0.15cm}\underline {\approx 0.541} \hspace{0.05cm}.$$ Zur Kontrolle verwenden wir $y = 0$: $$ x_{\rm max} = \frac{b}{a} = 2 \cdot {\rm J}_2 = 0.86 \hspace{0.05cm}.$$ Die Werte bei $x = 0$ sind somit: $$y_0 = \pm \sqrt{2} \cdot {\rm J}_1 \approx 0.735 \hspace{0.05cm}.$$