Aufgaben:Aufgabe 5.7Z: Anwendung der IDFT: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Realisierung von OFDM-Systemen }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice F…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1670__Mod_Z_5_7.png|right|]] |
| + | Bei der Diskreten Fouriertransformation (DFT) werden aus den Zeitabtastwerten $d(ν)$ mit der Laufvariablen ν = 0, ... , N – 1 die diskreten Spektralkoeffizienten D(μ) mit μ = 0, ... , N – 1 wie folgt berechnet: | ||
| + | $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | ||
| + | Hierbei ist mit w der komplexe Drehfaktor abgekürzt, der wie folgt definiert ist: | ||
| + | $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$ | ||
| + | Entsprechend gilt für die Inverse Diskrete Fouriertransformation (IDFT) als '''Umkehrfunktion''' der DFT: | ||
| + | $$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | ||
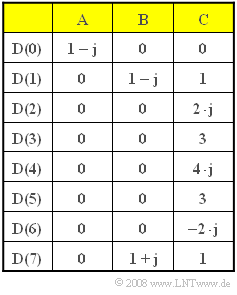
| + | In dieser Aufgabe sollen für verschiedene komplexwertige Beispielfolgen $D(μ)$ – die in der Tabelle mit „A”, „B” und „C” bezeichnet sind – die Zeitkoeffizienten d(ν) ermittelt werden. Es gilt somit stets N = 8. | ||
| + | |||
| + | '''Hinweis:''' Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von [http://www.lntwww.de/Modulationsverfahren/Realisierung_von_OFDM-Systemen Kapitel 5.6] dieses Buches und auf das [http://www.lntwww.de/Signaldarstellung/Diskrete_Fouriertransformation_(DFT) Kapitel 5.2] des Buches „Signaldarstellung”. Wir verweisen auch auf das Interaktionsmodul | ||
| + | |||
| + | Diskrete Fouriertransformation | ||
| + | |||
| Zeile 9: | Zeile 21: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie lauten die Zeitkoeffizienten $d(ν)$ für die Koeffizienten gemäß Spalte A? |
| − | |type=" | + | |type="{}"} |
| − | - | + | $D(μ)$ gemäß „A”: Re{$d(1)$} = { 1 3% } |
| − | + | im{$d(1)$} = { -1 3% } | |
| + | {Wie lauten die Zeitkoeffizienten $d(ν)$ für die Koeffizienten gemäß Spalte B? | ||
| + | |type="{}"} | ||
| + | $D(μ)$ gemäß „B”: Re{$d(1)$} = { 2.828 3% } | ||
| + | im{$d(1)$} = { 0 3% } | ||
| − | { | + | {Wie lauten die Zeitkoeffizienten $d(ν)$ für die Koeffizienten gemäß Spalte C? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $D(μ)$ gemäß „C”: Re{$d(1)$} = { -6.829 3% } |
| − | + | im{$d(1)$} = { -4 3% } | |
| Zeile 25: | Zeile 41: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Wegen $D(μ) = 0$ für μ ≠ 0 sind alle Zeitkoeffizienten $d(ν) = D(0)$. Damit gilt auch: |
| − | '''2.''' | + | $${\rm Re}\{d(1)\} \hspace{0.15cm}\underline {= 1}, \hspace{0.3cm}{\rm Im}\{d(1)\} \hspace{0.15cm}\underline {= -1}.$$ |
| − | '''3.''' | + | |
| − | + | '''2.''' Hier sind alle Spektralkoeffizienten 0 mit Ausnahme von $D_1 = 1 – j$ und $D_7 = 1 + j$. Daraus folgt für alle Zeitkoeffizienten (0 ≤ ν ≤ 7): | |
| − | + | $$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {7\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}.$$ | |
| − | + | Aufgrund der Periodizität gilt aber auch: | |
| − | + | $$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ +{\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}=$$ | |
| + | $$ = \left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} + {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right]+ {\rm{j}} \cdot\left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} - {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right].$$ | ||
| + | Mit dem Satz von Euler lässt sich dieser Ausdruck wie folgt umformen: | ||
| + | $$d(\nu) = 2 \cdot \cos \left( \frac {\pi}{4}\cdot \nu \right)+ 2 \cdot \sin \left( \frac {\pi}{4}\cdot \nu \right).$$ | ||
| + | Diese Zeitfunktion d(ν) ist rein reell und kennzeichnet eine harmonische Schwingung mit der Amplitude 2 mal „Wurzel aus 2” und der Phase φ = 45°. Der Zeitkoeffizient mit ν = 1 gibt das Maximum an: | ||
| + | $$ {\rm Re}[d(1)] = 2 \cdot \frac {\sqrt{2}}{2}+ 2 \cdot \frac {\sqrt{2}}{2} = 2 \cdot {\sqrt{2}} \hspace{0.15cm}\underline {\approx 2.828}, \hspace{0.5cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= 0}.$$ | ||
| + | |||
| + | '''3.''' Entsprechend der allgemeinen Gleichung gilt: | ||
| + | $$d(1) = \sum\limits_{\mu = 0}^{7} D(\mu)\cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\mu} =$$ | ||
| + | $$ = \left[ D(1) + D(7) \right]\cdot \cos \left( {\pi}/{4} \right) + \left[ D(3) + D(5) \right]\cdot \cos \left( {3\pi}/{4} \right)+$$ | ||
| + | $$ + {\rm j} \cdot \left[ D(2) - D(6) \right]\cdot \sin \left( {\pi}/{2} \right) + D(4) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}}.$$ | ||
| + | Die ersten drei Terme liefern rein reelle Ergebnisse: | ||
| + | $${\rm Re}\{d(1)\} = (1+1) \cdot \frac{1}{\sqrt{2}}-(3+3) \cdot \frac{1}{\sqrt{2}}+ {\rm j} \cdot4{\rm j} \cdot 1 =$$ | ||
| + | $$ = -\frac{4}{\sqrt{2}}-4\hspace{0.15cm}\underline { \approx -6.829}.$$ | ||
| + | Für den Imaginärteil ergibt sich: | ||
| + | $${\rm Im}\{d(1)\} = {\rm Im}\left\{4 \cdot{\rm j} \cdot (-1) \right\} \hspace{0.15cm}\underline {= -4}.$$ | ||
| + | |||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben Modulationsverfahren|^5.6 Realisierung von OFDM-Systemen^]] | + | [[Category:Aufgaben zu Modulationsverfahren|^5.6 Realisierung von OFDM-Systemen^]] |
Version vom 7. Januar 2017, 20:42 Uhr
Bei der Diskreten Fouriertransformation (DFT) werden aus den Zeitabtastwerten $d(ν)$ mit der Laufvariablen ν = 0, ... , N – 1 die diskreten Spektralkoeffizienten D(μ) mit μ = 0, ... , N – 1 wie folgt berechnet: $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ Hierbei ist mit w der komplexe Drehfaktor abgekürzt, der wie folgt definiert ist: $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$ Entsprechend gilt für die Inverse Diskrete Fouriertransformation (IDFT) als Umkehrfunktion der DFT: $$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ In dieser Aufgabe sollen für verschiedene komplexwertige Beispielfolgen $D(μ)$ – die in der Tabelle mit „A”, „B” und „C” bezeichnet sind – die Zeitkoeffizienten d(ν) ermittelt werden. Es gilt somit stets N = 8.
Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 5.6 dieses Buches und auf das Kapitel 5.2 des Buches „Signaldarstellung”. Wir verweisen auch auf das Interaktionsmodul
Diskrete Fouriertransformation
Fragebogen
Musterlösung
2. Hier sind alle Spektralkoeffizienten 0 mit Ausnahme von $D_1 = 1 – j$ und $D_7 = 1 + j$. Daraus folgt für alle Zeitkoeffizienten (0 ≤ ν ≤ 7): $$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {7\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}.$$ Aufgrund der Periodizität gilt aber auch: $$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ +{\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}=$$ $$ = \left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} + {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right]+ {\rm{j}} \cdot\left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} - {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right].$$ Mit dem Satz von Euler lässt sich dieser Ausdruck wie folgt umformen: $$d(\nu) = 2 \cdot \cos \left( \frac {\pi}{4}\cdot \nu \right)+ 2 \cdot \sin \left( \frac {\pi}{4}\cdot \nu \right).$$ Diese Zeitfunktion d(ν) ist rein reell und kennzeichnet eine harmonische Schwingung mit der Amplitude 2 mal „Wurzel aus 2” und der Phase φ = 45°. Der Zeitkoeffizient mit ν = 1 gibt das Maximum an: $$ {\rm Re}[d(1)] = 2 \cdot \frac {\sqrt{2}}{2}+ 2 \cdot \frac {\sqrt{2}}{2} = 2 \cdot {\sqrt{2}} \hspace{0.15cm}\underline {\approx 2.828}, \hspace{0.5cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= 0}.$$
3. Entsprechend der allgemeinen Gleichung gilt: $$d(1) = \sum\limits_{\mu = 0}^{7} D(\mu)\cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\mu} =$$ $$ = \left[ D(1) + D(7) \right]\cdot \cos \left( {\pi}/{4} \right) + \left[ D(3) + D(5) \right]\cdot \cos \left( {3\pi}/{4} \right)+$$ $$ + {\rm j} \cdot \left[ D(2) - D(6) \right]\cdot \sin \left( {\pi}/{2} \right) + D(4) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}}.$$ Die ersten drei Terme liefern rein reelle Ergebnisse: $${\rm Re}\{d(1)\} = (1+1) \cdot \frac{1}{\sqrt{2}}-(3+3) \cdot \frac{1}{\sqrt{2}}+ {\rm j} \cdot4{\rm j} \cdot 1 =$$ $$ = -\frac{4}{\sqrt{2}}-4\hspace{0.15cm}\underline { \approx -6.829}.$$ Für den Imaginärteil ergibt sich: $${\rm Im}\{d(1)\} = {\rm Im}\left\{4 \cdot{\rm j} \cdot (-1) \right\} \hspace{0.15cm}\underline {= -4}.$$