Kanalcodierung/Decodierung linearer Blockcodes: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{Header |Untermenü=Binäre Blockcodes zur Kanalcodierung |Vorherige Seite=Allgemeine Beschreibung linearer Blockcodes |Nächste Seite=Schranken für die Bl…“) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 29: | Zeile 29: | ||
::<math>\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ::<math>\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ||
d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | ||
| + | |||
| + | == Prinzip der Syndromdecodierung == | ||
| + | <br> | ||
| + | Vorausgesetzt wird hier ein (<i>n</i>, <i>k</i>)–Blockcode mit der Prüfmatrix <b>H</b> und den systematischen Codeworten | ||
| + | |||
| + | ::<math>\underline{x}\hspace{0.05cm} = (x_1, x_2, ... \hspace{0.05cm}, x_i, ... \hspace{0.05cm}, x_n) | ||
| + | = (u_1, u_2, ... \hspace{0.05cm}, u_k, p_1, ... \hspace{0.05cm}, p_{n-k})\hspace{0.05cm}. </math> | ||
| + | |||
| + | Mit dem Fehlervektor <i><u>e</u></i> gilt dann für das Empfangswort: | ||
| + | |||
| + | ::<math>\underline{y} = \underline{x} + \underline{e} \hspace{0.05cm}, \hspace{0.4cm} \underline{y} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.1cm} \underline{x} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.1cm} \underline{e} \in \hspace{0.1cm} {\rm GF}(2^n) | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | Ein Bitfehler an der Position <i>i</i>, das heißt <i>y<sub>i</sub></i> ≠ <i>x<sub>i</sub></i>, wird ausgedrückt durch den Fehlerkoeffizienten <i>e<sub>i</sub></i> = 1.<br> | ||
| + | |||
| + | {{Definition}}''':''' Das Syndrom <i><u>s</u></i> = (<i>s</i><sub>0</sub>, <i>s</i><sub>1</sub>, ... , <i>s</i><sub><i>m</i>–1</sub>) berechnet sich (als Zeilen– bzw. Spaltenvektor) aus dem Empfangswort <i><u>y</u></i> und der Prüfmatrix <b>H</b> in folgender Weise: | ||
| + | |||
| + | :<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T}\hspace{0.3cm}{\rm bzw.}\hspace{0.3cm} | ||
| + | \underline{s}^{\rm T} = { \boldsymbol{\rm H}} \cdot \underline{y}^{\rm T}\hspace{0.05cm}.</math> | ||
| + | |||
| + | Die Vektorlänge von <u><i>s</i></u> ist gleich <i>m</i> = <i>n</i> – <i>k</i> (Zeilenzahl von <b>H</b>).{{end}}<br> | ||
| + | |||
| + | Das Syndrom <i><u>s</u></i> zeigt folgende Charakteristika: | ||
| + | *Wegen <i><u>x</u></i> · <b>H</b><sup>T</sup> = <u>0</u> hängt <i><u>s</u></i> nicht vom Codewort <i><u>x</u></i> ab, sondern allein vom Fehlervektor <i><u>e</u></i>: | ||
| + | |||
| + | ::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} | ||
| + | = \hspace{0.05cm} \underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} + \hspace{0.05cm} \underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} | ||
| + | = \hspace{0.05cm} \underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Bei hinreichend wenig Bitfehlern liefert <i><u>s</u></i> einen eindeutigen Hinweis auf die Fehlerpositionen und ermöglicht so eine vollständige Fehlerkorrektur.<br><br> | ||
| + | |||
| + | {{Beispiel}}''':''' Ausgehend vom systematischen (7, 4, 3)–Hamming–Code erhält man beispielsweise für den Empfangsvektor <u><i>y</i></u> = (0, 1, 1, 1, 0, 0, 1) das folgende Ergebnis: | ||
| + | |||
| + | :<math>{ \boldsymbol{\rm H}} \cdot \underline{y}^{\rm T} | ||
| + | = \begin{pmatrix} | ||
| + | 1 &1 &1 &0 &1 &0 &0\\ | ||
| + | 0 &1 &1 &1 &0 &1 &0\\ | ||
| + | 1 &1 &0 &1 &0 &0 &1 | ||
| + | \end{pmatrix} \cdot \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 1 \\ | ||
| + | 1 \\ | ||
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | 1 | ||
| + | \end{pmatrix} = \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 1 \\ | ||
| + | 1 | ||
| + | \end{pmatrix} = \underline{s}^{\rm T} \hspace{0.05cm}.</math> | ||
| + | |||
| + | Vergleicht man das Syndrom mit den Prüfgleichungen des Hamming–Codes, so erkennt man, dass | ||
| + | *am wahrscheinlichsten das vierte Symbol (<i>x</i><sub>4</sub> = <i>u</i><sub>4</sub>) des Codewortes verfälscht wurde,<br> | ||
| + | |||
| + | *der Codewortschätzer somit das Ergebnis <u><i>z</i></u> = (0, 1, 1, 0, 0, 0, 1) liefern wird.<br> | ||
| + | |||
| + | *die Entscheidung nur dann richtig ist, wenn bei der Übertragung nur ein Bit verfälscht wurde.<br><br> | ||
| + | |||
| + | Nachfolgend sind die erforderlichen Korrekturen für den (7, 4, 3)–Hamming–Code angegeben, die sich aus dem errechneten Syndrom <i><u>s</u></i> entsprechend den Spalten der Prüfmatrix ergeben: | ||
| + | |||
| + | :<math>\underline{s} \hspace{-0.15cm} = \hspace{-0.15cm} (0, 0, 0) \hspace{0.10cm} \Rightarrow\hspace{0.10cm}{\rm keine\hspace{0.15cm} Korrektur}\hspace{0.05cm};\hspace{0.4cm}\underline{s} = (1, 0, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm}p_1{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};</math> | ||
| + | :<math>\underline{s} \hspace{-0.15cm} = \hspace{-0.15cm}(0, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} p_3{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{0.82cm}\underline{s} = (1, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_1{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};</math> | ||
| + | :<math>\underline{s} \hspace{-0.15cm} = \hspace{-0.15cm}(0, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} p_2{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{0.82cm}\underline{s} = (1, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_3{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};</math> | ||
| + | :<math>\underline{s} \hspace{-0.15cm} = \hspace{-0.15cm}(0, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_4{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{0.82cm}\underline{s} = (1, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_2{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm}. </math>{{end}}<br> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
{{Display}} | {{Display}} | ||
Version vom 9. Januar 2017, 22:35 Uhr
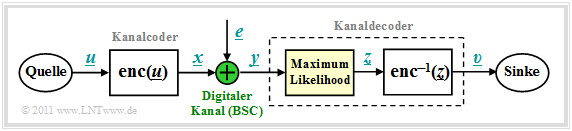
Blockschaltbild und Voraussetzungen
Wir gehen von dem bereits im Kapitel 1.2 gezeigten Blockschaltbild aus, wobei als Kanalmodell meist der Binary Symmetric Channel (BSC) verwendet wird. Zur Codewortschätzung verwenden wir den Maximum–Likelihood–Entscheider (ML), der für binäre Codes ⇒ x ∈ GF(2n) das gleiche Ergebnis liefert wie der MAP–Empfänger.
Die Aufgabe des Kanaldecoders kann wie folgt beschrieben werden:
- Der Vektor υ nach der Decodierung (an der Sinke) soll möglichst gut mit dem Informationswort u übereinstimmen. Das heißt: Die Blockfehlerwahrscheinlichkeit soll möglichst klein sein:
- \[{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]
- Aufgrund der deterministischen Zuweisungen x = enc(u) bzw. υ = enc–1(z) gilt aber auch:
- \[{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{z} \ne \underline{x}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]
- Gesucht ist somit das zum gegebenen Empfangswort y = x + e am wahrscheinlichsten gesendete Codewort xi, das als Ergebnis z weiter gegeben wird:
- \[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.\]
- Beim BSC–Kanal gilt sowohl xi ∈ GF(2n) als auch y ∈ GF(2n), so dass die ML–Regel auch mit der Hamming–Distanz dH(y, xi) geschrieben werden kann:
- \[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]
Prinzip der Syndromdecodierung
Vorausgesetzt wird hier ein (n, k)–Blockcode mit der Prüfmatrix H und den systematischen Codeworten
- \[\underline{x}\hspace{0.05cm} = (x_1, x_2, ... \hspace{0.05cm}, x_i, ... \hspace{0.05cm}, x_n) = (u_1, u_2, ... \hspace{0.05cm}, u_k, p_1, ... \hspace{0.05cm}, p_{n-k})\hspace{0.05cm}. \]
Mit dem Fehlervektor e gilt dann für das Empfangswort:
- \[\underline{y} = \underline{x} + \underline{e} \hspace{0.05cm}, \hspace{0.4cm} \underline{y} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.1cm} \underline{x} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.1cm} \underline{e} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}.\]
Ein Bitfehler an der Position i, das heißt yi ≠ xi, wird ausgedrückt durch den Fehlerkoeffizienten ei = 1.
\[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T}\hspace{0.3cm}{\rm bzw.}\hspace{0.3cm} \underline{s}^{\rm T} = { \boldsymbol{\rm H}} \cdot \underline{y}^{\rm T}\hspace{0.05cm}.\]
Die Vektorlänge von s ist gleich m = n – k (Zeilenzahl von H).
Das Syndrom s zeigt folgende Charakteristika:
- Wegen x · HT = 0 hängt s nicht vom Codewort x ab, sondern allein vom Fehlervektor e:
- \[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} = \hspace{0.05cm} \underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} + \hspace{0.05cm} \underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} = \hspace{0.05cm} \underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} \hspace{0.05cm}.\]
- Bei hinreichend wenig Bitfehlern liefert s einen eindeutigen Hinweis auf die Fehlerpositionen und ermöglicht so eine vollständige Fehlerkorrektur.
\[{ \boldsymbol{\rm H}} \cdot \underline{y}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} = \underline{s}^{\rm T} \hspace{0.05cm}.\]
Vergleicht man das Syndrom mit den Prüfgleichungen des Hamming–Codes, so erkennt man, dass
- am wahrscheinlichsten das vierte Symbol (x4 = u4) des Codewortes verfälscht wurde,
- der Codewortschätzer somit das Ergebnis z = (0, 1, 1, 0, 0, 0, 1) liefern wird.
- die Entscheidung nur dann richtig ist, wenn bei der Übertragung nur ein Bit verfälscht wurde.
Nachfolgend sind die erforderlichen Korrekturen für den (7, 4, 3)–Hamming–Code angegeben, die sich aus dem errechneten Syndrom s entsprechend den Spalten der Prüfmatrix ergeben:
\[\underline{s} \hspace{-0.15cm} = \hspace{-0.15cm} (0, 0, 0) \hspace{0.10cm} \Rightarrow\hspace{0.10cm}{\rm keine\hspace{0.15cm} Korrektur}\hspace{0.05cm};\hspace{0.4cm}\underline{s} = (1, 0, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm}p_1{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\] \[\underline{s} \hspace{-0.15cm} = \hspace{-0.15cm}(0, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} p_3{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{0.82cm}\underline{s} = (1, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_1{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\] \[\underline{s} \hspace{-0.15cm} = \hspace{-0.15cm}(0, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} p_2{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{0.82cm}\underline{s} = (1, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_3{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\]
\[\underline{s} \hspace{-0.15cm} = \hspace{-0.15cm}(0, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_4{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{0.82cm}\underline{s} = (1, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_2{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm}. \]