Kanalcodierung/Algebraische und polynomische Beschreibung: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 386: | Zeile 386: | ||
Auf der nächsten Seite werden diese Definitionen und Gesetzmäßigkeiten an einem ausführlichen Beispiel verdeutlicht.<br> | Auf der nächsten Seite werden diese Definitionen und Gesetzmäßigkeiten an einem ausführlichen Beispiel verdeutlicht.<br> | ||
| + | |||
| + | == Übertragungsfunktionsmatrix – Transfer Function Matrix (2) == | ||
| + | <br> | ||
| + | {{Beispiel}}''':''' | ||
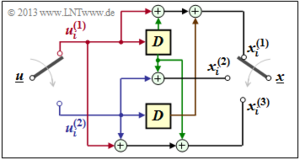
| + | [[Datei:P ID2617 KC T 3 1 S4 v1.png|rahmenlos|rechts|Faltungscoder mit <i>k</i> = 2, <i>n</i> = 3 und <i>m</i> = 1]] Wir betrachten nun wieder den (<i>n</i> = 3, <i>k</i> = 2, <i>m</i> = 1)–Faltungscoder, dessen Teilmatrizen in einem früheren Beispiel wie folgt ermittelt wurden: | ||
| + | |||
| + | :<math>{ \boldsymbol{\rm G}}_0 = | ||
| + | \begin{pmatrix} | ||
| + | 1 & 0 & 1\\ | ||
| + | 0 & 1 & 1 | ||
| + | \end{pmatrix} \hspace{0.05cm}, \\ | ||
| + | { \boldsymbol{\rm G}}_1 = \begin{pmatrix} | ||
| + | 1 & 1 & 1\\ | ||
| + | 1 & 0 & 0 | ||
| + | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| + | |||
| + | Wegen <i>m</i> = 1 existieren keine Teilmatrizen für <i>l</i> ≥ 2. Damit lautet die Übertragungsfunktionsmatrix: | ||
| + | |||
| + | :<math>{\boldsymbol{\rm G}}(D) = {\boldsymbol{\rm G}}_0 + {\boldsymbol{\rm G}}_1 \cdot D = | ||
| + | \begin{pmatrix} | ||
| + | 1+D & D & 1+D\\ | ||
| + | D & 1 & 1 | ||
| + | \end{pmatrix} | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | Die (zeitlich begrenzte) Informationssequenz sei <u><i>u</i></u> = (0, 1, 1, 0, 0, 0, 1, 1), woraus sich die beiden Eingangsfolgen wie folgt ergeben: | ||
| + | |||
| + | :<math>\underline{u}^{(1)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | ||
| + | {U}^{(1)}(D) = D + D^3 \hspace{0.05cm},</math> | ||
| + | :<math>\underline{u}^{(2)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | ||
| + | {U}^{(2)}(D) = 1 + D^3 \hspace{0.05cm}.</math> | ||
| + | |||
| + | Daraus folgt für den Vektor der <i>D</i>–Transformierten am Coderausgang: | ||
| + | |||
| + | :<math>\underline{X}(D) \hspace{-0.15cm} = \hspace{-0.15cm} \big (\hspace{0.05cm} {X}^{(1)}(D)\hspace{0.05cm}, \hspace{0.05cm} {X}^{(2)}(D)\hspace{0.05cm}, \hspace{0.05cm} {X}^{(3)}(D)\hspace{0.05cm}\big ) = \underline{U}(D) \cdot {\boldsymbol{\rm G}}(D)</math> | ||
| + | :<math>\hspace{1cm} = \hspace{-0.15cm} \begin{pmatrix} | ||
| + | D+D^3 & 1+D^3 | ||
| + | \end{pmatrix} \cdot \begin{pmatrix} | ||
| + | 1+D & D & 1+D\\ | ||
| + | D & 1 & 1 | ||
| + | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| + | |||
| + | Damit ergeben sich in den drei Strängen folgende Codesquenzen: | ||
| + | |||
| + | :<math>{X}^{(1)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (D + D^3) \cdot (1+D) + (1 + D^3) \cdot D =</math> | ||
| + | :<math>\hspace{1.5cm} = \hspace{-0.15cm} D + D^2 + D^3 + D^4 + D + D^4 = D^2 + D^3</math> | ||
| + | |||
| + | :<math>\Rightarrow \underline{x}^{(1)} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm},</math> | ||
| + | |||
| + | :<math>{X}^{(2)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (D + D^3) \cdot D + (1 + D^3) \cdot 1 =</math> | ||
| + | :<math>\hspace{1.5cm} = \hspace{-0.15cm} D^2 + D^4 + 1 + D^3 = 1+D^2 + D^3 + D^4</math> | ||
| + | |||
| + | :<math>\Rightarrow \underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm},</math> | ||
| + | |||
| + | :<math>{X}^{(3)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (D + D^3) \cdot (1 + D) + (1 + D^3) \cdot 1 =</math> | ||
| + | :<math>\hspace{1.5cm} = \hspace{-0.15cm} D + D^2 + D^3+ D^4 + 1 + D^3 = 1+ D + D^2 + D^4</math> | ||
| + | |||
| + | :<math>\Rightarrow \underline{x}^{(3)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm}.</math> | ||
| + | |||
| + | Die gleichen Ergebnisse haben wir auf anderen Wegen bereits in vorherigen Beispielen erhalten: | ||
| + | * im Beispiel von Kapitel 3.1, Seite 4.<br> | ||
| + | |||
| + | *im Beispiel von Kapitel 3.2, Seite 2.{{end}}<br> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Version vom 15. Januar 2017, 16:35 Uhr
Inhaltsverzeichnis
- 1 Definition und Interpretation der Teilmatrizen G0, ... , Gm
- 2 Generatormatrix eines Faltungscodierers mit Gedächtnis m
- 3 Generatormatrix für Faltungscodierer der Rate 1/n
- 4 GF(2)–Beschreibungsformen eines Digitalen Filters (1)
- 5 GF(2)–Beschreibungsformen eines Digitalen Filters (2)
- 6 Anwendung der D–Transformation auf Rate–1/n–Faltungscoder (1)
- 7 Anwendung der D–Transformation auf Rate–1/n–Faltungscoder (2)
- 8 Übertragungsfunktionsmatrix – Transfer Function Matrix (1)
- 9 Übertragungsfunktionsmatrix – Transfer Function Matrix (2)
Definition und Interpretation der Teilmatrizen G0, ... , Gm
Entsprechend den Ausführungen in Kapitel 1.4 lässt sich das Codewort x eines linearen Blockcodes aus dem Informationswort u und der Generatormatrix G in einfacher Weise ermitteln:
\[\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.\]
Dabei gilt:
- Die Vektoren u und x haben die Länge k (Bitanzahl eines Informationswortes) bzw. n (Bitanzahl eines Codewortes) und G besitzt die Dimension k × n (k Zeilen und n Spalten).
- Bei Faltungscodierung bezeichnen dagegen u und x Sequenzen mit k' → ∞ und n' → ∞. Deshalb wird auch die Generatormatrix G in beiden Richtungen unendlich weit ausgedehnt sein.
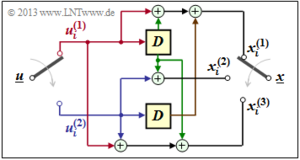
Als Vorbereitung für die Einführung der Generatormatrix G auf der nächsten Seite definieren wir m + 1 Teilmatrizen, jeweils mit k Zeilen und n Spalten, die wir mit Gl bezeichnen, wobei 0 ≤ l ≤ m gilt.
Diese Definition wird nun an einem Beispiel verdeutlicht.
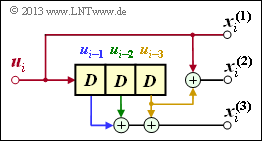
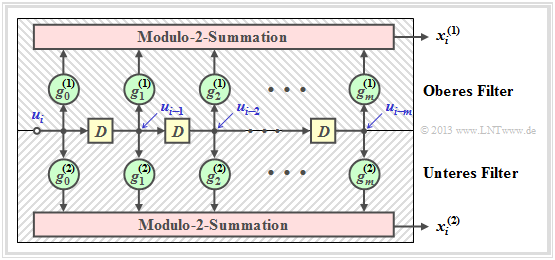
\[x_i^{(1)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},\] \[x_i^{(2)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(2)} + u_{i-1}^{(1)} \hspace{0.05cm},\] \[x_i^{(3)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)}+ u_{i-1}^{(1)} \hspace{0.05cm}.\]
Wegen der Gedächtnisordnung m = 1 wird dieser Codierer durch die beiden Teilmatrizen G0 und G1 charakterisiert:
\[{ \boldsymbol{\rm G}}_0 = \begin{pmatrix} 1 & 0 & 1\\ 0 & 1 & 1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm} { \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 & 1 & 1\\ 1 & 0 & 0 \end{pmatrix}\hspace{0.05cm}.\]
Diese Matrizen sind wie folgt zu interpretieren:
- Erste Zeile von G0, rote Pfeile: ui(1) beeinflusst sowohl xi(1) als auch xi(3), nicht jedoch xi(2).
- Zweite Zeile von G0, blaue Pfeile: ui(2) beeinflusst xi(2) und xi(3), aber nicht xi(1).
- Erste Zeile von G1, grüne Pfeile: ui–1(1) beeinflusst alle drei Coderausgänge.
- Zweite Zeile von G1, brauner Pfeil: ui–1(2) beeinflusst nur xi(1).
Generatormatrix eines Faltungscodierers mit Gedächtnis m
Mit den Teilmatrizen G0, ... , Gm lassen sich die n Codebits zum Zeitpunkt i wie folgt ausdrücken:
\[\underline{x}_i = \sum_{l = 0}^{m} \hspace{0.15cm}\underline{u}_{i-l} \cdot { \boldsymbol{\rm G}}_l = \underline{u}_{i} \cdot { \boldsymbol{\rm G}}_0 + \underline{u}_{i-1} \cdot { \boldsymbol{\rm G}}_1 + ... + \underline{u}_{i-m} \cdot { \boldsymbol{\rm G}}_m \hspace{0.05cm}.\]
Hierbei sind folgende vektorielle Größen zu berücksichtigen:
\[\underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, \hspace{0.05cm}... \hspace{0.1cm}, u_i^{(k)}\right )\hspace{0.05cm},\hspace{0.5cm} \underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, \hspace{0.05cm}... \hspace{0.1cm}, x_i^{(n)}\right )\hspace{0.05cm}.\]
Betrachtet man die bei i = 1 beginnenden und sich zeitlich bis ins Unendliche erstreckenden Sequenzen
\[\underline{\it u} = \big( \underline{\it u}_1\hspace{0.05cm}, \underline{\it u}_2\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm}, \underline{\it u}_i\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm} \big)\hspace{0.05cm},\hspace{0.5cm} \underline{\it x} = \big( \underline{\it x}_1\hspace{0.05cm}, \underline{\it x}_2\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm}, \underline{\it x}_i\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm} \big)\hspace{0.05cm},\]
so kann dieser Zusammenhang durch die Matrixgleichung x = u · G ausgedrückt werden. Hierbei ist für die Generatormatrix G zu setzen:
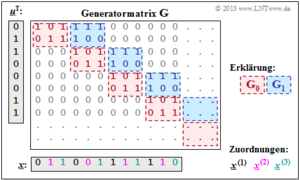
\[{ \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \cdots & \cdots & & & \cdots \end{pmatrix}\hspace{0.05cm}.\]
Aus der Gleichung erkennt man sofort das Gedächtnis m des Faltungscodes. Die Parameter k und n sind direkt nicht ablesbar. Sie sind aber durch die Zeilen– und Spaltenzahl der Teilmatrizen Gl festgelegt.
Anzumerken ist:
- Die Generatormatrix G erstreckt sich nach unten und nach rechts eigentlich bis ins Unendliche. Explizit dargestellt sind aber nur 8 Zeilen und 12 Spalten.
- Für die zeitlich begrenzte Informationssequenz u = (0, 1, 1, 0, 0, 0, 1, 1) ist der gezeichnete Matrixteil ausreichend. Die Codesequenz lautet dann: x = (0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0).
- Anhand der Beschriftungsfarben lassen sich die n = 3 Codewortstränge ablesen. Das gleiche Ergebnis haben wir (auf anderem Wege) im Beispiel am Ende von Kapitel 3.1 erhalten.
- \[\underline{\it x}^{(1)} = (0\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(2)} = (1\hspace{0.05cm}, 0\hspace{0.05cm},1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(3)} = (1\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0) \hspace{0.05cm}.\]
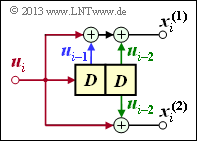
Generatormatrix für Faltungscodierer der Rate 1/n
Wir betrachten nun den Sonderfall k = 1, zum einen aus Gründen einer möglichst einfachen Darstellung, aber auch, weil Faltungscodierer der Rate 1/n für die Praxis eine große Bedeutung besitzen.
Faltungscodierer mit k = 1, n = 2 und m = 1
Aus der nebenstehenden Skizze kann abgeleitet werden:
\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 0 & 1 \end{pmatrix}\]
\[\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}=\begin{pmatrix} 11 & 01 & 00 & 00 & 00 & \cdots & \\ 00 & 11 & 01 & 00 & 00 & \cdots & \\ 00 & 00 & 11 & 01 & 00 & \cdots & \\ 00 & 00 & 00 & 11 & 01 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm}.\]
Für die Eingangssequenz u = (1, 0, 1, 1) beginnt die Codesequenz mit x = (1, 1, 0, 1, 1, 1, 1, 0, ...). Dieses Ergebnis ist gleich der Summe der Zeilen 1, 3 und 4 der Gewneratormatrix.
Faltungscodierer mit k = 1, n = 2 und m = 2
Aufgrund der Gedächtnisordnung m = 2 gibt es hier drei Teilmatrizen:
\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 1 & 0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_2=\begin{pmatrix} 1 & 1 \end{pmatrix}\]
\[\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}=\begin{pmatrix} 11 & 10 & 11 & 00 & 00 & 00 & \cdots & \\ 00 & 11 & 10 & 11 & 00 & 00 & \cdots & \\ 00 & 00 & 11 & 10 & 11 & 00 & \cdots & \\ 00 & 00 & 00 & 11 & 10 & 11 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm}.\]
Hier führt die Eingangsssequenz u = (1, 0, 1, 1) zur Codesequenz x = (1, 1, 1, 0, 0, 0, 0, 1, ...).
Faltungscodierer mit k = 1, n = 3 und m = 3
Wegen m = 3 gibt es vier Teilmatrizen der Dimension 1 × 3:
\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 & 0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\]
\[{ \boldsymbol{\rm G}}_2=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_3=\begin{pmatrix} 0 & 1 & 1 \end{pmatrix}\hspace{0.05cm}.\]
Damit lautet die resultierende Generatormatrix:
\[{ \boldsymbol{\rm G}}=\begin{pmatrix} 110 & 001 & 001 & 011 & 000 & 000 & 000 & \cdots & \\ 000 & 110 & 001 & 001 & 011 & 000 & 000 & \cdots & \\ 000 & 000 & 110 & 001 & 001 & 011 & 000 & \cdots & \\ 000 & 000 & 000 & 110 & 001 & 001 & 011 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm},\]
und man erhält für u = (1, 0, 1, 1) die Codesequenz x = (1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, ...).
GF(2)–Beschreibungsformen eines Digitalen Filters (1)
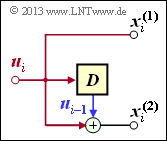
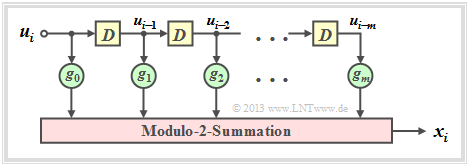
In Kapitel 3.1 wurde bereits darauf hingewiesen, dass ein Faltungscodierer der Rate 1/n durch mehrere Digitale Filter realisiert werden kann, wobei die Filter parallel mit der gleichen Eingangsfolge u arbeiten. Bevor wir diese Aussage vertiefen, sollen zuerst die Eigenschaften eines Digitalfilters für das Galoisfeld GF(2) genannt werden.
Die Grafik ist wie folgt zu interpretieren:
- Das Filter besitzt die Impulsantwort g = (g0, g1, g2, ... , gm), wobei für alle Filterkoeffizienten (mit den Indizes 0 ≤ l ≤ m) gilt: gl ∈ GF(2) = {0, 1}.
- Die einzelnen Symbole ui der Eingangsfolge u seien ebenfalls binär: ui ∈ {0, 1}. Damit gilt für das Ausgangssymbol zu den Zeitpunkten i ≥ 1 mit Addition und Multiplikation in GF(2):
- \[x_i = \sum_{l = 0}^{m} g_l \cdot u_{i-l} \hspace{0.05cm}.\]
- Dies entspricht der (zeitdiskreten) Faltungsoperation (englisch: Convolution), gekennzeichnet durch einen Stern. Damit kann für die gesamte Ausgangssequenz geschrieben werden:
- \[\underline{x} = \underline{u} * \underline{g}\hspace{0.05cm}.\]
- Wesentlicher Unterschied gegenüber dem Kapitel 5.2 des Buches „Stochastische Signaltheorie” ist die Modulo–2–Addition (1 + 1 = 0) anstelle der herkömmlichen Addition (1 + 1 = 2).
Die Eingangssequenz dieses Filters sei zeitlich unbegrenzt: u = (1, 1, 0, 0, 0, ...).
Damit ergibt sich die (unendliche) Ausgangssequenz x im binären Galoisfeld ⇒ GF(2):
\[\underline{x} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0, \hspace{0.05cm}. ... \hspace{0.05cm}) * (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1\hspace{0.05cm})= \] \[\hspace{0.3cm} = \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm}0,\hspace{0.05cm} . ... \hspace{0.05cm}) \oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm}0, \hspace{0.05cm} . ... \hspace{0.05cm}) = (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, . ... \hspace{0.05cm}) \hspace{0.05cm}.\]
Bei der herkömmlichen Faltung (für reelle Zahlen) hätte dagegen das Ergebnis gelautet:
\[\underline{x}= (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 2,\hspace{0.05cm} 1,\hspace{0.05cm} 0, . ... \hspace{0.05cm}) \hspace{0.05cm}.\]
GF(2)–Beschreibungsformen eines Digitalen Filters (2)
Zeitdiskrete Signale kann man auch durch Polynome bezüglich einer Dummy–Variablen repräsentieren.
\[X(D) = x_0 + x_1 \cdot D + x_2 \cdot D^2 + \hspace{0.05cm}...\hspace{0.05cm}= \sum_{i = 0}^{\infty} x_i \cdot D^i \hspace{0.05cm}.\]
Für diese spezielle Transformation in einen Bildbereich verwenden wir auch die Notation:
\[\underline{x} = (x_0, x_1, x_2,\hspace{0.05cm}...\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad X(D) = \sum_{i = 0}^{\infty} x_i \cdot D^i \hspace{0.05cm}.\]
In der Literatur wird manchmal x(D) anstelle von X(D) verwendet. Wir schreiben in LNTwww aber alle Bildbereichsfunktionen mit Großbuchstaben, zum Beispiel Fourier–, Laplace– und D–Transformation:
\[x(t) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}}\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)\hspace{0.05cm},\hspace{0.4cm} x(t) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\hspace{0.15cm} X(p) \hspace{0.05cm},\hspace{0.4cm} \underline{x} \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} X(D) \hspace{0.05cm}.\]
Wir werden nun die D–Transformation auch auf die Informationssequenz u und die Impulsantwort g an. Aufgrund der zeitlichen Begrenzung von g ergibt sich die obere Summationsgrenze bei G(D) zu i = m:
\[\underline{u} = (u_0, u_1, u_2,\hspace{0.05cm}...\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = \sum_{i = 0}^{\infty} u_i \cdot D^i \hspace{0.05cm},\]
\[\underline{g} = (g_0, g_1, \hspace{0.05cm}...\hspace{0.05cm}, g_m) \quad
\circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad
G(D) = \sum_{i = 0}^{m} g_i \cdot D^i \hspace{0.05cm}.\]
\[\underline{x} = \underline{u} * \underline{g} \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad X(D) = U(D) \cdot G(D) \hspace{0.05cm}.\]
Man bezeichnet, wie in der Systemtheorie allgemein üblich, auch die D–Transformierte G(D) der Impulsantwort g als Übertragungsfunktion (englisch: Transfer Function).
Der (recht einfache) Beweis dieses wichtigen Ergebnisses finden Sie in der Angabe zu Aufgabe Z3.3.
\[\underline{u} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}...\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = 1+ D \hspace{0.05cm},\]
\[\underline{g} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D^2 + D^3 \hspace{0.05cm}.\]
Wie im letzten Biespiel: erhält man auch auf diesem Lösungsweg:
\[X(D) \hspace{-0.15cm} = \hspace{-0.15cm} U(D) \cdot G(D) = (1+D) \cdot (1+ D^2 + D^3) =\] \[\hspace{1cm} = \hspace{-0.15cm} 1+ D^2 + D^3 +D + D^3 + D^4 = 1+ D + D^2 + D^4 \]
\[\Rightarrow \hspace{0.4cm} \underline{x} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, ... \hspace{0.05cm}) \hspace{0.05cm}.\]
Die Multiplikation mit D im Bildbereich entspricht im Zeitbereich einer Verschiebung um eine Stelle nach rechts, weshalb man D als Verzögerungsoperator (englisch: Delay Operator) bezeichnet:
\[W(D) = D \cdot X(D) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\circ\quad \underline{w} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, ... \hspace{0.05cm}) \hspace{0.05cm}.\]
Anwendung der D–Transformation auf Rate–1/n–Faltungscoder (1)
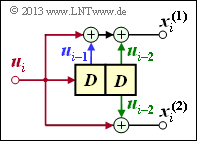
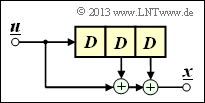
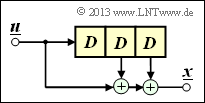
Wir wenden nun die Ergebnisse der letzten Seite auf einen Faltungscoder an, wobei wir uns zunächst auf den Sonderfall k = 1 beschränken. Ein solcher (n, k = 1)–Faltungscode lässt sich mit n Digitalen Filtern realisieren, die auf der gleichen Informationssequenz u parallel arbeiten. Die Grafik zeigt die Anordnung für den Codeparameter n = 2 ⇒ Coderate R = 1/2.
Die nachfolgenden Gleichungen gelten für beide Filter gleichermaßen, wobei für das obere Filter j = 1 und für das untere Filter j = 2 zu setzen ist:
- Die Impulsantworten der beiden Filter ergeben sich zu
- \[\underline{g}^{(j)} = (g_0^{(j)}, g_1^{(j)}, \hspace{0.05cm}...\hspace{0.05cm}, g_m^{(j)}\hspace{0.01cm}) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]
- Die beiden Ausgangssequenzen lauten:
- \[\underline{x}^{(j)} = (x_0^{(j)}, x_1^{(j)}, x_2^{(j)}, \hspace{0.05cm}...\hspace{0.05cm}) = \underline{u} \cdot \underline{g}^{(j)} \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]
- Hierbei ist berücksichtigt, dass das obere Filter und das untere Filter beide auf der gleichen Eingangssequenz u = (u0, u1, u2, ...) arbeiten.
- Für die D–Transformierten der Ausgangssequenzen gilt:
- \[X^{(j)}(D) = U(D) \cdot G^{(j)}(D) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]
Auf der nächsten Seite verwenden wir eine kompaktere Schreibweise.
Anwendung der D–Transformation auf Rate–1/n–Faltungscoder (2)
Um den soeben dargelegten Sachverhalt kompakter darstellen zu können, definieren wir nun folgende vektorielle Größen eines Faltungscodes der Rate 1/n:
\[\underline{G}(D) = \left ( G^{(1)}(D), G^{(2)}(D), \hspace{0.05cm}...\hspace{0.1cm}, G^{(n)} (D) \right )\hspace{0.05cm}.\]
Der Vektor X(D) beinhaltet die D–Transformierten der n Codesequenzen x(1), x(2), ... , x(n):
\[\underline{X}(D) = \left ( X^{(1)}(D), X^{(2)}(D), \hspace{0.05cm}...\hspace{0.1cm}, X^{(n)} (D) \right )\hspace{0.05cm}.\]
Damit erhält man die folgende Vektorgleichung:
\[\underline{X}(D) = U(D) \cdot \underline{G}(D)\hspace{0.05cm}.\]
Aufgrund des Codeparameters k = 1 ist U(D) hier keine vektorielle Größe.
\[\underline{g}^{(1)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D + D^2 \hspace{0.05cm},\] \[\underline{g}^{(2)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D^2 \]
\[\Rightarrow \hspace{0.3cm} \underline{G}(D) = \big ( 1+ D + D^2 \hspace{0.05cm}, \hspace{0.1cm}1+ D^2 \big )\hspace{0.05cm}.\]
Die Informationssequenz sei u = (1, 0, 1, 1), was zur D–Transformierten U(D) = 1 + D2 + D3 führt. Damit erhält man
\[\underline{X}(D) = \left ( X^{(1)}(D),\hspace{0.1cm} X^{(2)}(D) \right ) = U(D) \cdot \underline{G}(D) \hspace{0.05cm}, \hspace{0.2cm}\]
wobei
\[{X}^{(1)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (1+ D^2 + D^3) \cdot (1+ D + D^2)=\] \[\hspace{1.5cm} = \hspace{-0.15cm}1+ D + D^2 + D^2 + D^3 + D^4 + D^3 + D^4 + D^5 = 1+ D + D^5\]
\[\Rightarrow \underline{x}^{(1)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} ... \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm},\]
\[{X}^{(2)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (1+ D^2 + D^3) \cdot (1+ D^2)=\] \[\hspace{1.5cm} = \hspace{-0.15cm}1+ D^2 + D^2 + D^4 + D^3 + D^5 = 1+ D^3 + D^4 + D^5\]
\[\Rightarrow \underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} ... \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm}.\]
Das gleiche Ergebnis haben wir in der Aufgabe Z3.1 auf anderem Wege erhalten. Nach dem Multplexen der beiden Sränge erhält man wieder: x = (11, 10, 00, 01, 01, 11, 00, 00, ... ).
Übertragungsfunktionsmatrix – Transfer Function Matrix (1)
Auf der letzten Seite haben wir gesehen, dass ein Faltungscode der Rate 1/n sich am kompaktesten als Vektorgleichung im D–transformierten Bereich beschreiben lässt:
\[\underline{X}(D) = U(D) \cdot \underline{G}(D)\hspace{0.05cm}.\]
Nun erweitern wir das Resultat auf Faltungscodierer mit mehr als einem Eingang ⇒ k≥ 2 (siehe Grafik).
Um einen Faltungscode der Rate k/n im D–Bereich abbilden zu können, muss die Dimension obiger Vektorgleichung hinsichtlich Eingang und Übertragungsfunktion erhöht werden:
\[\underline{X}(D) = \underline{U}(D) \cdot { \boldsymbol{\rm G}}(D)\hspace{0.05cm},\]
mit folgenden Maßnahmen:
- Aus der skalaren Funktion U(D) wird der Vektor U(D) = (U(1)(D), U(2)(D), ... , U(k)(D)).
- Aus dem Vektor G(D) wird die k×n–Matrix G(D), die man als Übertragungsfunktionsmatrix bezeichnet (englisch: Transfer Function Matrix oder auch Polynomial Generator Matrix):
- \[{\boldsymbol{\rm G}}(D)=\begin{pmatrix} G_1^{(1)}(D) & G_1^{(2)}(D) & \ldots & G_1^{(n)}(D)\\ G_2^{(1)}(D) & G_2^{(2)}(D) & \ldots & G_2^{(n)}(D)\\ \vdots & \vdots & & \vdots\\ G_k^{(1)}(D) & G_k^{(2)}(D) & \ldots & G_k^{(n)}(D) \end{pmatrix}\hspace{0.05cm}.\]
- Jedes der k·n Matrixelemente Gi(j)(D) mit 1 ≤ i ≤ k, 1 ≤ j ≤ n ist ein Polynom über der Dummy–Variablen D im Galoisfeld GF(2), maximal vom Grad m, wobei m das Gedächtnis angibt.
- Für die obige Übertragungsfunktionsmatrix kann mit den zu Beginn dieses Kapitels definierten Teilmatrizen G0, ... , Gm auch geschrieben werden (als Index verwenden wir wieder l):
- \[{\boldsymbol{\rm G}}(D) = \sum_{l = 0}^{m} {\boldsymbol{\rm G}}_l \cdot D\hspace{0.03cm}^l = {\boldsymbol{\rm G}}_0 + {\boldsymbol{\rm G}}_1 \cdot D + {\boldsymbol{\rm G}}_2 \cdot D^2 + ... \hspace{0.05cm}+ {\boldsymbol{\rm G}}_m \cdot D\hspace{0.03cm}^m \hspace{0.05cm}.\]
Auf der nächsten Seite werden diese Definitionen und Gesetzmäßigkeiten an einem ausführlichen Beispiel verdeutlicht.
Übertragungsfunktionsmatrix – Transfer Function Matrix (2)
\[{ \boldsymbol{\rm G}}_0 = \begin{pmatrix} 1 & 0 & 1\\ 0 & 1 & 1 \end{pmatrix} \hspace{0.05cm}, \\ { \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 & 1 & 1\\ 1 & 0 & 0 \end{pmatrix}\hspace{0.05cm}.\]
Wegen m = 1 existieren keine Teilmatrizen für l ≥ 2. Damit lautet die Übertragungsfunktionsmatrix:
\[{\boldsymbol{\rm G}}(D) = {\boldsymbol{\rm G}}_0 + {\boldsymbol{\rm G}}_1 \cdot D = \begin{pmatrix} 1+D & D & 1+D\\ D & 1 & 1 \end{pmatrix} \hspace{0.05cm}.\]
Die (zeitlich begrenzte) Informationssequenz sei u = (0, 1, 1, 0, 0, 0, 1, 1), woraus sich die beiden Eingangsfolgen wie folgt ergeben:
\[\underline{u}^{(1)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad {U}^{(1)}(D) = D + D^3 \hspace{0.05cm},\] \[\underline{u}^{(2)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad {U}^{(2)}(D) = 1 + D^3 \hspace{0.05cm}.\]
Daraus folgt für den Vektor der D–Transformierten am Coderausgang:
\[\underline{X}(D) \hspace{-0.15cm} = \hspace{-0.15cm} \big (\hspace{0.05cm} {X}^{(1)}(D)\hspace{0.05cm}, \hspace{0.05cm} {X}^{(2)}(D)\hspace{0.05cm}, \hspace{0.05cm} {X}^{(3)}(D)\hspace{0.05cm}\big ) = \underline{U}(D) \cdot {\boldsymbol{\rm G}}(D)\] \[\hspace{1cm} = \hspace{-0.15cm} \begin{pmatrix} D+D^3 & 1+D^3 \end{pmatrix} \cdot \begin{pmatrix} 1+D & D & 1+D\\ D & 1 & 1 \end{pmatrix}\hspace{0.05cm}.\]
Damit ergeben sich in den drei Strängen folgende Codesquenzen:
\[{X}^{(1)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (D + D^3) \cdot (1+D) + (1 + D^3) \cdot D =\] \[\hspace{1.5cm} = \hspace{-0.15cm} D + D^2 + D^3 + D^4 + D + D^4 = D^2 + D^3\]
\[\Rightarrow \underline{x}^{(1)} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm},\]
\[{X}^{(2)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (D + D^3) \cdot D + (1 + D^3) \cdot 1 =\] \[\hspace{1.5cm} = \hspace{-0.15cm} D^2 + D^4 + 1 + D^3 = 1+D^2 + D^3 + D^4\]
\[\Rightarrow \underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm},\]
\[{X}^{(3)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (D + D^3) \cdot (1 + D) + (1 + D^3) \cdot 1 =\] \[\hspace{1.5cm} = \hspace{-0.15cm} D + D^2 + D^3+ D^4 + 1 + D^3 = 1+ D + D^2 + D^4\]
\[\Rightarrow \underline{x}^{(3)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm}.\]
Die gleichen Ergebnisse haben wir auf anderen Wegen bereits in vorherigen Beispielen erhalten:
- im Beispiel von Kapitel 3.1, Seite 4.
- im Beispiel von Kapitel 3.2, Seite 2.