Aufgaben:Aufgabe 1.4: 2S/3E-Kanalmodell

• Zurück zum Buch

Ein Sender gibt die binären Symbole $\rm L$ (Ereignis $S_{\rm L}$) und $H$ (Ereignis $S_{\rm H}$) ab.

• Bei guten Bedingungen entscheidet sich der Digitalempfänger ebenfalls nur für die Binärsymbole $\rm L$ (Ereignis $E_{\rm L}$) oder $H$ (Ereignis $E_{\rm H}$) .
• Kann der Empfänger allerdings vermuten, dass bei der Übertragung ein Fehler aufgetreten ist, so trifft er keine Entscheidung (Ereignis $E_{\rm K}$; $K$ steht dabei für „Keine Entscheidung”).

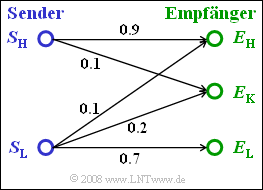
Die Grafik zeigt ein einfaches Kanalmodell in Form von Übergangswahrscheinlichkeiten. Es ist zu erkennen, dass ein gesendetes $\rm L$ durchaus als Symbol $\rm H$ empfangen werden kann. Dagegen ist der Übergang von $\rm H$ nach $\rm L$ nicht möglich.

Die Symbolauftrittswahrscheinlichkeiten am Sender seien ${\rm Pr}(S_{\rm L}) = 0.3$ und ${\rm Pr}(S_{\rm H}) = 0.7$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Statistische Abhängigkeit und Unabhängigkeit.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:

Statistische Abhängigkeit und Unabhängigkeit

Fragebogen

1

Wie groß ist die Wahrscheinlichkeit dafür, dass sich der Empfänger für das Symbol $\rm L$ entscheidet?

${\rm Pr}(E_{\rm L}) \ = $

2

Wie groß ist die Wahrscheinlichkeit dafür, dass sich der Empfänger für das Symbol $\rm H$ entscheidet?

${\rm Pr}(E_{\rm H}) \ = $

3

Wie groß ist die Wahrscheinlichkeit dafür, dass der Empfänger keine Entscheidung trifft?

${\rm Pr}(E_{\rm K}) \ = $

4

Mit welcher Wahrscheinlichkeit entscheidet der Empfänger falsch?

$\text{Pr(falsche Entscheidung)} \ = $

5

Wie groß ist die Wahrscheinlichkeit, dass das Symbol $\rm L$ gesendet wurde, wenn sich der Empfänger für das Symbol $\rm L$ entschieden hat?

${\rm Pr}(E_{\rm S}\hspace{0.05cm}|\hspace{0.05cm}E_{\rm L} ) \ = $

6

Wie groß ist die Wahrscheinlichkeit, dass das Symbol $\rm L$ gesendet wurde, wenn der Empfänger keine Entscheidung trifft?

${\rm Pr}(E_{\rm S}\hspace{0.05cm}|\hspace{0.05cm}E_{\rm K} ) \ =$

Musterlösung

Musterlösung

1.   Nur wenn das Symbol L gesendet wurde, kann sich der Empfänger beim gegebenen Kanal für das Symbol L entscheiden. Die Wahrscheinlichkeit für ein empfangenes L ist allerdings um den Faktor 0.7 kleiner als für ein gesendetes. Daraus folgt:

$$\rm Pr (\it E_{\rm L}) = \rm Pr (\it S_{\rm L}) \cdot \rm Pr (\it E_{\rm L}|\it S_{\rm L}) = \rm 0.3 \cdot 0.7 \hspace{0.15cm}\underline {= \rm 0.21}.$$

2.   Zum Ereignis E_H kommt man sowohl von S_H als auch von S_L aus. Deshalb gilt:

$$\rm Pr (\it E_{\rm H}) = \rm Pr (\it S_{\rm H}) \cdot \rm Pr (\it E_{\rm H}|\it S_{\rm H}) + \rm Pr (\it S_{\rm L}) \cdot\rm Pr (\it E_{\rm H}|\it S_{\rm L}) \\ = \rm 0.7 \cdot 0.9 + 0.3 \cdot 0.1\hspace{0.15cm}\underline { = \rm 0.66}.$$

3.   Die Ereignisse E_H, E_L und E_K bilden zusammen ein vollständiges System. Daraus folgt:

$$\rm Pr (\it E_{\rm K}) =\rm 1 - \rm Pr (\it E_{\rm L}) - \rm Pr (\it E_{\rm H}) \hspace{0.15cm}\underline {= \rm 0.13}.$$

4.   Eine falsche Entscheidung kann man mengentheoretisch wie folgt charakterisieren:

$$\rm Pr (falsche\hspace{0.1cm}Entscheidung) = Pr (\it S_{\rm L} \cap \it E_{\rm H} \cup \it S_{\rm H} \cap \it E_{\rm L}) = \rm 0.3 \cdot 0.1 + 0.7\cdot 0 \hspace{0.15cm}\underline {= \rm 0.03}.$$

5.   Wenn das Symbol L empfangen wurde, kann nur L gesendet worden sein. Daraus folgt:

$$\rm Pr (\it S_{\rm L} | \it E_{\rm L}) \hspace{0.15cm}\underline {= \rm 1}.$$

6.   Zur Lösung dieser Aufgabe eignet sich z. B. der Satz von Bayes:

$$\rm Pr (\it S_{\rm L}|\it E_{\rm K}) =\frac{ \rm Pr (\it E_{\rm K} | S_{\rm L}) \cdot \rm Pr (\it S_{\rm L})}{\rm Pr (\it E_{\rm K})} =\frac{ \rm 0.2 \cdot 0.3}{\rm 0.13} = \frac{\rm 6}{\rm 13}\hspace{0.15cm}\underline { \approx \rm 0.462}.$$