Aufgaben:Aufgabe 3.8: Verstärkung und Begrenzung

• Zurück zum Buch

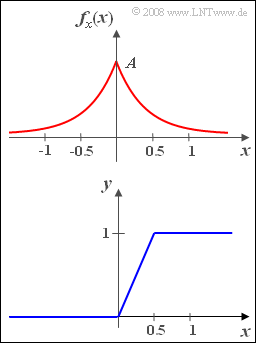
Wir betrachtenein Zufallssignal $x(t)$ mit symmetrischer Wahrscheinlichkeitsdichtefunktion:

$$f_x(x)=A\cdot \rm e^{\rm -2 \hspace{0.05cm}\cdot \hspace{0.05cm}|\it x|}.$$

Dieses Signal wird an den Eingang einer Nichtlinearität mit der Kennlinie (siehe unteres Bild) angelegt: $$y=\left\{\begin{array}{*{4}{c}}0 &\rm f\ddot{u}r\hspace{0.2cm} \it x <\rm 0, \\\rm2\it x & \rm f\ddot{u}r\hspace{0.2cm} \rm 0\le \it x\le \rm 0.5, \\1 & \rm f\ddot{u}r\hspace{0.2cm}\it x > \rm 0.5\\\end{array}\right.$$

Das Ausgangssignal wird mit $y(t)$ bezeichnet.

Diese unten skizzierte Kennlinie begrenzt die Größe $x(t)$ am Eingang asymmetrisch und verstärkt sie im linearen Bereich.

Hinweise:

• Die Aufgabe gehört zum Kapitel Exponentialverteilte Zufallsgröße.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Gegeben ist das folgende bestimmte Integral:

$$\int_{0}^{\infty}\it x^n\cdot\rm e^{-\it a x}\, d{\it x} =\frac{\it n!}{\it a^{n}}.$$

Fragebogen

1

Berechnen Sie den Funktionswert A = f_x(0) der WDF an der Stelle x = 0.

$A$ =

2

Berechnen Sie die Momente m_k der Zufallsgröße x. Begründen Sie, dass alle Momente mit ungeradem Index null sind. Wie groß ist die Streuung?

$\sigma_x$ =

3

Welcher Wert ergibt sich für die Kurtosis der Zufallsgröße x?

$K_x$ =

4

Wie groß ist die Wahrscheinlichkeit, dass x den Wert 0.5 überschreitet?

$Pr(x > 0.5)$ =

5

Welche der folgenden Aussagen sind bezüglich der WDF f_y(y) zutreffend?

	Die WDF beinhaltet eine Diracfunktion bei y = 0.
	Die WDF beinhaltet eine Diracfunktion bei y = 0.5.
	Die WDF beinhaltet eine Diracfunktion bei y = 1.

6

Wie lautet der kontinuierliche Anteil der WDF f_y(y)? Welcher Wert ergibt sich für y = 0.5?

$f_y(y\ =\ 0.5)$ =

7

Wie groß ist der Mittelwert der begrenzten und verstärkten Zufallsgröße y?

$m_y$ =

Musterlösung

Musterlösung

1.  Die Fläche unter der Wahrscheinlichkeitsdichtefunktion ergibt

$$\it F=\rm 2\cdot \it A\int_{\rm 0}^{\infty}\hspace{-0.15cm}\rm e^{\rm -2\it x}\, \rm d \it x=\frac{\rm 2\cdot \it A}{\rm -2}\cdot \rm e^{\rm -2\it x}\Big|_{\rm 0}^{\infty}=\it A.$$

Da diese Fläche definitionsgemäß gleich 1 sein muss, gilt A = 1.

2.  Alle Momente mit ungeradem Index k sind aufgrund der symmetrischen WDF gleich Null. Bei geradem k kann der linke Teil der WDF in den rechten gespiegelt werden und man erhält:

$$\it m_k=\rm 2 \cdot \int_{\rm 0}^{\infty}\hspace{-0.15cm}\it x^{k}\cdot \rm e^{-\rm 2\it x}\,\rm d \it x=\frac{\rm 2\cdot\rm\Gamma(\it k+\rm 1)}{\rm 2^{\it k+\rm 1}}=\frac{\it k!}{\rm 2^{\it k}}.$$

Daraus folgt mit k = 2 unter Berücksichtigung des Mittelwertes m₁ = 0:

$$m_{\rm 2}=\frac{\rm 2!}{\rm 2^2}=\rm 0.5\hspace{0.5cm}bzw.\hspace{0,5cm} \it\sigma_x=\sqrt{\it m_{\rm 2}}\hspace{0.15cm}\underline{=\rm 0.707}.$$

3.  Das Zentralmoment vierter Ordnung ist μ₄ = m₄ = 4!/2⁴ = 1.5. Daraus folgt für die Kurtosis:

$$\it K_{\it x}=\frac{\it \mu_{\rm 4}}{\it \sigma_{\it x}^{\rm 4}}=\frac{\rm 1.5}{\rm 0.25}\hspace{0.15cm}\underline{=\rm 6}.$$

4.  Mit dem Ergebnis aus 1. erhält man:

$$\rm Pr(\it x>\rm 0.5)=\int_{\rm 0.5}^{\infty}\rm e^{-\rm 2\it x}\,\rm d \it x=\frac{\rm 1}{\rm 2\rm e}\hspace{0.15cm}\underline{=\rm 0.184}.$$

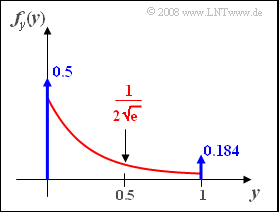
5.  Die WDF f_y(y) beinhaltet eine Diracfunktion an der Stelle y = 0 mit dem Gewicht Pr(x < 0) = 0.5 und zudem eine weitere Diracfunktion bei y = 1 mit dem Gewicht Pr(x > 0.5)  = 0.184. Richtig sind somit die Lösungsvorschläge 1 und 3.

6.  Der Signalbereich 0 ≤ x ≤ 0.5 wird am Ausgang auf den Bereich 0 ≤ y ≤ 1 linear abgebildet. Die Ableitung der Kennlinie ist hier konstant gleich 2 (Verstärkung). Daraus erhält man:

$$f_y(y)=\frac{f_x(x)}{|g'(x)|}\Bigg|_{x=h(y)}=\frac{\rm e^{-\rm 2\it x}}{\rm 2}\Bigg|_{\it x={\it y}/{\rm 2}}=0.5 \cdot {\rm e^{\it -y}} .$$

Bei y = 0.5 beträgt dementsprechend der kontinuierliche WDF-Anteil etwa 0.304.

7.  Für den Mittelwert der Zufallsgröße y gilt:

$$m_y=\frac{1}{\rm 2\rm e} \cdot 1 +\int\limits_{\rm 0}^{\rm 1}\frac{\it y}{\rm 2}\cdot \rm e^{\it -y}\, \rm d \it y=\frac{\rm 1}{\rm 2\rm e}+\frac{\rm 1}{\rm 2}-\frac{\rm 1}{\rm e}=\frac{\rm 1}{\rm 2}-\frac{\rm 1}{\rm 2 e}\hspace{0.15cm}\underline{=\rm 0.316}.$$

Der erste Term stammt vom Dirac bei y = 1, der zweite vom kontinuierlichen WDF–Anteil.