Aufgaben:Aufgabe 4.3Z: Diracförmige 2D-WDF: Unterschied zwischen den Versionen
| Zeile 67: | Zeile 67: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Richtig sind <u>die beiden ersten Antworten</u>: | |
| − | + | *Die Randwahrscheinlichkeitsdichtefunktion $f_{x}(x)$ erhält man aus der 2D–WDF $f_{xy}(x, y)$ durch Integration über $y$. | |
| + | *Für alle möglichen Werte $ x \in \{-2, -1, 0, +1, +2\}$ sind die Wahrscheinlichkeiten gleich $0.2$. | ||
| + | *Es gilt ${\rm Pr}(x \le 1)= 0.8$ und der Mittelwert ist $m_x = 0$. | ||
| − | |||
| − | :< | + | [[Datei:P_ID258__Sto_Z_4_3_b.png|right|Diskrete Rand-WDF]] |
| − | + | '''(2)''' Richtig sind <u>die Lösungsvorschläge 2 und 3</u>: | |
| + | *Durch Integration über $x$ erhält man die rechts skizzierte WDF $f_{y}(y)$. | ||
| + | * Aufgrund der Symmetrie ergibt sich der Mittelwert $m_y = 0$. | ||
| + | *Die gesuchte Wahrscheinlichkeit ist ${\rm Pr}(y \le 1)= 0.9$. | ||
| − | |||
| − | |||
| − | + | '''(3)''' Definitionsgemäß gilt: | |
| + | $$F_{xy}(r_x, r_y) = \rm Pr((\it x \le r_x)\cap(\it y\le r_y)).$$ | ||
| − | + | Für $r_x = r_y = 1$ folgt daraus: | |
| − | + | $$F_{xy}(+1, +1) = {\rm Pr}((x \le 1)\cap(y\le 1)).$$ | |
| − | + | Wie aus der 2D–WDF auf der Angabenseite zu ersehen, ist diese Wahrscheinlichkeit ${\rm Pr}((x \le 1)\cap(y\le 1))\hspace{0.15cm}\underline{=0.8}$. | |
| − | |||
| − | |||
| − | + | '''(4)''' Hierfür kann mit dem Satz von Bayes auch geschrieben werden: | |
| − | + | $$ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = \frac{ \rm Pr((\it x \le \rm 1)\cap(\it y\le \rm 1))}{ \rm Pr(\it y\le \rm 1)} = \it \frac{F_{xy}(\rm 1, \rm 1)}{F_{y}(\rm 1)}.$$ | |
| − | |||
| − | + | Mit den Ergebnissen aus (2) und (3) folgt daraus $ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = 0.8/0.9 = 8/9 \hspace{0.15cm}\underline{=0.889}$. | |
| − | |||
| − | |||
| − | + | '''(5)''' Entsprechend der Definition gilt für das gemeinsame Moment: | |
| − | + | $$m_{xy} = {\rm E}[x\cdot y] = \sum\limits_{i} {\rm Pr}( x_i \cap y_i)\cdot x_i\cdot y_i. $$ | |
| − | : | + | Es verbleiben fünf Diracfunktionen mit $x_i \cdot y_i \ne 0$: |
| + | $$m_{xy} = \rm 0.1\cdot (-2) (-1) + 0.2\cdot(-1) (-1)+ 0.2\cdot 1\cdot 1 + 0.1\cdot 2\cdot 1+ 0.1\cdot 2\cdot 2\hspace{0.15cm}\underline{=\rm 1.2}.$$ | ||
| − | : | + | |
| + | [[Datei:P_ID259__Sto_Z_4_3_f.png|right|2D-WDF]] | ||
| + | '''(6)''' Für den Korrelationskoeffizienten gilt: | ||
| + | $$\rho_{xy} = \frac{\mu_{xy}}{\sigma_x\cdot \sigma_y} = \frac{1.2}{\sqrt{2}\cdot\sqrt{1.4}}\hspace{0.15cm}\underline{=0.717}.$$ | ||
| + | |||
| + | Hier ist berücksichtigt, dass wegen $m_x = m_y = 0$ die Kovarianz $\mu_{xy}$ gleich dem Moment $m_{xy}$ ist. | ||
| + | |||
| + | Die Gleichung der Korrelationsgeraden lautet: | ||
| + | $$y=\frac{\sigma_y}{\sigma_x}\cdot \rho_{xy}\cdot x = \frac{\mu_{xy}}{\sigma_x^{\rm 2}}\cdot x = \rm 0.6\cdot \it x.$$ | ||
| + | |||
| + | Im Bild ist die Gerade $y = K(x)$ eingezeichnet. Der Winkel zwischen Korrelationsgerade und $x$-Achse beträgt $\theta_{y\hspace{0.05cm}→\hspace{0.05cm} x} = \arctan(0.6) \hspace{0.15cm}\underline{=31^\circ}.$ | ||
| + | |||
| + | '''(7)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | ||
| + | *Bei statistischer Unabhängigkeit müsste $f_{xy}(x, y) = f_{x}(x) \cdot f_{y}(y)$ gelten, was hier nicht erfüllt ist. | ||
| + | *Aus der Korreliertheit (folgt aus $\rho_{xy} \ne 0$) kann direkt auf die statistische Abhängigkeit geschlossen werden, denn Korrelation bedeutet eine Sonderform der statistischen Abhängigkeit, nämlich die lineare statistische Abhängigkeit. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 19. März 2017, 15:05 Uhr
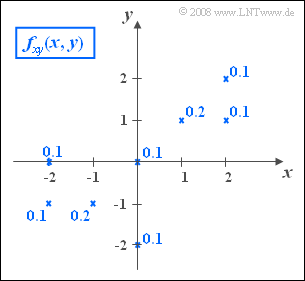
In der Grafik ist die zweidimensionale Wahrscheinlichkeitsdichtefunktion $f_{xy}(x, y)$ der zwei diskreten Zufallsgrößen $x$ und $y$ dargestellt.
- Diese 2D–WDF besteht aus acht Diracpunkten, durch Kreuze markiert. Die Zahlenwerte geben die entsprechenden Wahrscheinlichkeiten an.
- Es ist zu erkennen, dass sowohl $x$ als auch $y$ alle ganzzahligen Werte zwischen den Grenzen $-2$ und $+2$ annehmen können.
- Die Varianzen der beiden Zufallsgrößen sind wie folgt gegeben: $\sigma_x^2 = 2$, $\sigma_y^2 = 1.4$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Zufallsgrößen.
- Bezuig genommen wird auch auf das Kapitel Momente einer diskreten Zufallsgröße
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- Die Randwahrscheinlichkeitsdichtefunktion $f_{x}(x)$ erhält man aus der 2D–WDF $f_{xy}(x, y)$ durch Integration über $y$.
- Für alle möglichen Werte $ x \in \{-2, -1, 0, +1, +2\}$ sind die Wahrscheinlichkeiten gleich $0.2$.
- Es gilt ${\rm Pr}(x \le 1)= 0.8$ und der Mittelwert ist $m_x = 0$.
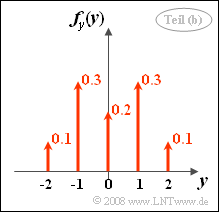
(2) Richtig sind die Lösungsvorschläge 2 und 3:
- Durch Integration über $x$ erhält man die rechts skizzierte WDF $f_{y}(y)$.
- Aufgrund der Symmetrie ergibt sich der Mittelwert $m_y = 0$.
- Die gesuchte Wahrscheinlichkeit ist ${\rm Pr}(y \le 1)= 0.9$.
(3) Definitionsgemäß gilt:
$$F_{xy}(r_x, r_y) = \rm Pr((\it x \le r_x)\cap(\it y\le r_y)).$$
Für $r_x = r_y = 1$ folgt daraus: $$F_{xy}(+1, +1) = {\rm Pr}((x \le 1)\cap(y\le 1)).$$
Wie aus der 2D–WDF auf der Angabenseite zu ersehen, ist diese Wahrscheinlichkeit ${\rm Pr}((x \le 1)\cap(y\le 1))\hspace{0.15cm}\underline{=0.8}$.
(4) Hierfür kann mit dem Satz von Bayes auch geschrieben werden:
$$ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = \frac{ \rm Pr((\it x \le \rm 1)\cap(\it y\le \rm 1))}{ \rm Pr(\it y\le \rm 1)} = \it \frac{F_{xy}(\rm 1, \rm 1)}{F_{y}(\rm 1)}.$$
Mit den Ergebnissen aus (2) und (3) folgt daraus $ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = 0.8/0.9 = 8/9 \hspace{0.15cm}\underline{=0.889}$.
(5) Entsprechend der Definition gilt für das gemeinsame Moment:
$$m_{xy} = {\rm E}[x\cdot y] = \sum\limits_{i} {\rm Pr}( x_i \cap y_i)\cdot x_i\cdot y_i. $$
Es verbleiben fünf Diracfunktionen mit $x_i \cdot y_i \ne 0$: $$m_{xy} = \rm 0.1\cdot (-2) (-1) + 0.2\cdot(-1) (-1)+ 0.2\cdot 1\cdot 1 + 0.1\cdot 2\cdot 1+ 0.1\cdot 2\cdot 2\hspace{0.15cm}\underline{=\rm 1.2}.$$
(6) Für den Korrelationskoeffizienten gilt: $$\rho_{xy} = \frac{\mu_{xy}}{\sigma_x\cdot \sigma_y} = \frac{1.2}{\sqrt{2}\cdot\sqrt{1.4}}\hspace{0.15cm}\underline{=0.717}.$$
Hier ist berücksichtigt, dass wegen $m_x = m_y = 0$ die Kovarianz $\mu_{xy}$ gleich dem Moment $m_{xy}$ ist.
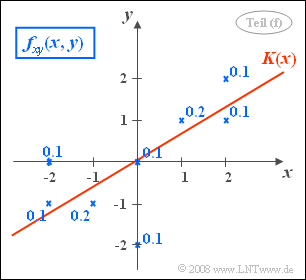
Die Gleichung der Korrelationsgeraden lautet: $$y=\frac{\sigma_y}{\sigma_x}\cdot \rho_{xy}\cdot x = \frac{\mu_{xy}}{\sigma_x^{\rm 2}}\cdot x = \rm 0.6\cdot \it x.$$
Im Bild ist die Gerade $y = K(x)$ eingezeichnet. Der Winkel zwischen Korrelationsgerade und $x$-Achse beträgt $\theta_{y\hspace{0.05cm}→\hspace{0.05cm} x} = \arctan(0.6) \hspace{0.15cm}\underline{=31^\circ}.$
(7) Richtig sind die Lösungsvorschläge 2 und 3:
- Bei statistischer Unabhängigkeit müsste $f_{xy}(x, y) = f_{x}(x) \cdot f_{y}(y)$ gelten, was hier nicht erfüllt ist.
- Aus der Korreliertheit (folgt aus $\rho_{xy} \ne 0$) kann direkt auf die statistische Abhängigkeit geschlossen werden, denn Korrelation bedeutet eine Sonderform der statistischen Abhängigkeit, nämlich die lineare statistische Abhängigkeit.