Aufgaben:Aufgabe 4.7Z: Zum Water–Filling–Algorithmus

• Zurück zum Buch

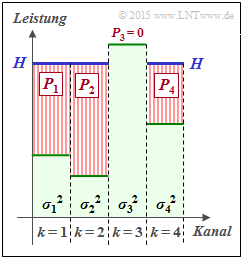
Wir betrachten K parallele Gaußsche Kanäle (AWGN) mit unterschiedlichen Störleistungen σ_k² (1 ≤ k ≤ K), wie in der nebenstehenden Grafik am Beispiel K = 4 verdeutlicht ist. Die Sendeleistung in den einzelnen Kanälen wird mit P_k bezeichnet, deren Summe den vorgegebenen Wert P_X nicht überschreiten darf: $$P_1 + ... \hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$ Sind die Zufallsgrößen X₁, ..., X_k gaußisch, so kann für die (gesamte) Transinformation zwischen dem Eingang X und dem Ausgang Y geschrieben werden: $$I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K) = 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_k}{\sigma_k^2})\hspace{0.05cm},\hspace{0.5cm} {\rm Ergebnis\hspace{0.15cm} in \hspace{0.15cm} bit} \hspace{0.05cm}.$$ Das Maximum hierfür ist die Kanalkapazität des Gesamtsystems, wobei sich die Maximierung auf die Aufteilung der Gesamtleistung P_X auf die einzelnen Kanäle bezieht. $$C_K(P_X) = \max_{P_k\hspace{0.05cm},\hspace{0.15cm}{\rm mit} \hspace{0.15cm}P_1 + ... \hspace{0.05cm}+ P_K = P_X} \hspace{-0.5cm} I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K) \hspace{0.05cm}.$$ Diese Maximierung kann mit dem Water–Filling–Algorithmus geschehen, der in obiger Grafik für K = 4 dargestellt ist. Eine genaue Beschreibung finden Sie im Theorieteil In der vorliegenden Aufgabe soll dieser Algorithmus angewendet werden, wobei von folgenden Voraussetzungen auszugehen ist:

• Zwei parallele Gaußkanäle  ⇒  K = 2,
• Normierte Störleistungen σ₁² = 1 und σ₂² = 4,
• Normierte Sendeleistungen P_X = 10 bzw. P_X = 3.

Hinweis: Die Aufgabe bezieht sich auf das Themengebiet von Kapitel 4.2.

Fragebogen

1

Welche Strategien der Leistungszuteilung sind sinnvoll?

	Einem stark gestörten Kanal k (mit großer Störleistung σk2) sollte eine große Nutzleistung Pk zugewiesen werden.
	Einem stark gestörten Kanal k (mit großer Störleistung σk2) sollte nur eine kleine Nutzleistung Pk zugewiesen werden.
	Bei K gleich guten Kanälen  ⇒  σ12 = ... = σK2 = σN2 sollte die Leistung gleichmäßig verteilt werden.

2

Welche Transinformation I = I(X₁, X₂; Y₁, Y₂) ergibt sich, wenn man die Sendeleistung P_X = 10 gleichmäßig auf beide Kanäle verteilt?

$P1 = P2 = 5: I$ =

3

Es gelte weiter P_X = 10. Welche optimale Leistungsaufteilung ergibt sich nach dem Water–Filling–Algorithmus?

$PX = 10: P1$ =

$P1 = P2 = 5: I$ =

4

Wie groß ist die Kanalkapazität für K = 2 und P_X = 10?

$C2(PX = 10)$ =

5

Welche Ergebnisse erhält man mit K = 2 und P_X = 3?

$P1 = P2 = 1.5: I$ =

$C2(PX = 3)$ =

Musterlösung

Musterlösung

1. 2. 3. 4. 5. 6. 7.