Stochastische Signaltheorie/Wiener–Kolmogorow–Filter: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==Optimierungskriterium des Wiener–Kolmogorow–Filters== | ==Optimierungskriterium des Wiener–Kolmogorow–Filters== | ||
| − | Als weiteres Beispiel zur Optimalfilterung betrachten wir nun die Aufgabenstellung, die Form eines Nutzsignals $s(t)$ aus dem durch additives Rauschen $n(t)$ gestörten Empfangssignals $r(t)$ im Sinne des mittleren quadratischen Fehlers (MQF) möglichst gut zu rekonstruieren: | + | Als weiteres Beispiel zur Optimalfilterung betrachten wir nun die Aufgabenstellung, die Form eines Nutzsignals $s(t)$ aus dem durch additives Rauschen $n(t)$ gestörten Empfangssignals $r(t)$ im Sinne des ''mittleren quadratischen Fehlers'' (MQF) möglichst gut zu rekonstruieren: |
$${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t} \mathop = \limits^! {\rm{Minimum}}.$$ | $${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t} \mathop = \limits^! {\rm{Minimum}}.$$ | ||
| Zeile 14: | Zeile 14: | ||
Für diese Optimierungsaufgabe gelten folgende Voraussetzungen: | Für diese Optimierungsaufgabe gelten folgende Voraussetzungen: | ||
*Das zu rekonstruierende Signal $s(t)$ ist das Ergebnis eines Zufallsprozesses { $s(t)$}, von dem nur die statistischen Eigenschaften in Form des Leistungsdichtespektrums ${\it Φ}_s(f)$ bekannt ist. | *Das zu rekonstruierende Signal $s(t)$ ist das Ergebnis eines Zufallsprozesses { $s(t)$}, von dem nur die statistischen Eigenschaften in Form des Leistungsdichtespektrums ${\it Φ}_s(f)$ bekannt ist. | ||
| − | *Das Störsignal $n(t)$ ist durch das LDS ${\it Φ}_n(f)$ gegeben. Korrelationen zwischen dem Nutz– und dem Störsignal berücksichtigen die | + | *Das Störsignal $n(t)$ ist durch das LDS ${\it Φ}_n(f)$ gegeben. Korrelationen zwischen dem Nutz– und dem Störsignal berücksichtigen die [[Stochastische_Signaltheorie/Kreuzkorrelationsfunktion_und_Kreuzleistungsdichte#Kreuzleistungsdichtespektrum|Kreuzleistungsdichtespektren]] ${\it Φ}_{sn}(f) = \hspace{0.1cm} –{ {\it Φ}_{ns} }^∗(f).$ |
*Das Ausgangssignal des gesuchten Filters ist mit $d(t)$ bezeichnet, das sich entsprechend des MQF möglichst wenig von $d(t)$ unterscheiden soll. $T_{\rm M}$ bezeichnet wiederum die Messdauer. | *Das Ausgangssignal des gesuchten Filters ist mit $d(t)$ bezeichnet, das sich entsprechend des MQF möglichst wenig von $d(t)$ unterscheiden soll. $T_{\rm M}$ bezeichnet wiederum die Messdauer. | ||
| − | |||
| − | |||
:[[Datei:P_ID650__Sto_T_5_5_S1_neu.png | Zur Herleitung des Wiener-Filters]] | :[[Datei:P_ID650__Sto_T_5_5_S1_neu.png | Zur Herleitung des Wiener-Filters]] | ||
| − | + | Das Signal $s(t)$ sei mittelwertfrei $(m_s = 0)$ und leistungsbegrenzt. Das bedeutet: Die Signalenergie $E_s$ ist aufgrund der unendlichen Ausdehnung des Signals $s(t)$ unendlich und die Signalleistung besitzt einen endlichen Wert: | |
| − | Das Signal $s(t)$ sei mittelwertfrei $(m_s = | + | :$$P_s = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {s(t)^2 \, {\rm{d}}t > 0.}$$ |
| − | $$P_s = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {s(t)^2 \, {\rm{d}}t > 0.}$$ | ||
Ein grundsätzlicher Unterschied zur Aufgabenstellung beim Matched–Filter ist das stochastische und leistungsbegrenzte Nutzsignal $s(t)$. Erinnern wir uns: Beim Matched–Filter war das zu rekonstruierende Signal $g(t)$ deterministisch, zeitlich begrenzt und damit auch energiebegrenzt. | Ein grundsätzlicher Unterschied zur Aufgabenstellung beim Matched–Filter ist das stochastische und leistungsbegrenzte Nutzsignal $s(t)$. Erinnern wir uns: Beim Matched–Filter war das zu rekonstruierende Signal $g(t)$ deterministisch, zeitlich begrenzt und damit auch energiebegrenzt. | ||
| Zeile 29: | Zeile 26: | ||
==Ergebnis der Filteroptimierung== | ==Ergebnis der Filteroptimierung== | ||
A. Kolmogorow und N. Wiener haben dieses Optimierungsproblem nahezu zur gleichen Zeit unabhängig voneinander gelöst. Die Übertragungsfunktion des optimalen Filters kann über die so genannte ''Wiener-Hopfsche Integralgleichung'' ermittelt werden, und lautet: | A. Kolmogorow und N. Wiener haben dieses Optimierungsproblem nahezu zur gleichen Zeit unabhängig voneinander gelöst. Die Übertragungsfunktion des optimalen Filters kann über die so genannte ''Wiener-Hopfsche Integralgleichung'' ermittelt werden, und lautet: | ||
| − | $$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) + {\it \Phi }_{ns} (f)} }{ { {\it \Phi }_s (f) + {\it \Phi }_{sn} (f) + {\it \Phi }_{ns} (f) + {\it \Phi }_n (f)}}.$$ | + | :$$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) + {\it \Phi }_{ns} (f)} }{ { {\it \Phi }_s (f) + {\it \Phi }_{sn} (f) + {\it \Phi }_{ns} (f) + {\it \Phi }_n (f)}}.$$ |
| − | Der Index „WF” steht für Wiener-Filter und lässt leider die Verdienste von Kolmogorow nicht erkennen. Auf die exakte, mathematische Ableitung der Gleichung wird hier verzichtet. Vielmehr soll | + | Der Index „WF” steht für Wiener-Filter und lässt leider die Verdienste von Kolmogorow nicht erkennen. Auf die exakte, mathematische Ableitung der Gleichung wird hier verzichtet. Vielmehr soll dieses Filter im Folgenden an einigen Sonderfällen verdeutlicht und interpretiert werden. |
*Sind Signal und Störung unkorreliert ⇒ ${\it Φ}_{sn}(f) = {\it Φ}_{ns}(f) =$ 0, so vereinfacht sich die obige Gleichung wie folgt: | *Sind Signal und Störung unkorreliert ⇒ ${\it Φ}_{sn}(f) = {\it Φ}_{ns}(f) =$ 0, so vereinfacht sich die obige Gleichung wie folgt: | ||
| − | $$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) }}{{ {\it \Phi }_s (f) + {\it \Phi }_n (f) }} = \frac{1}{{1 + {\it \Phi }_n (f) / {\it \Phi }_s (f) }}.$$ | + | :$$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) }}{{ {\it \Phi }_s (f) + {\it \Phi }_n (f) }} = \frac{1}{{1 + {\it \Phi }_n (f) / {\it \Phi }_s (f) }}.$$ |
*Das Filter wirkt dann wie ein frequenzabhängiger Teiler, wobei das Teilerverhältnis durch die Leistungsdichtespektren von Nutzsignal und Störsignal bestimmt wird. | *Das Filter wirkt dann wie ein frequenzabhängiger Teiler, wobei das Teilerverhältnis durch die Leistungsdichtespektren von Nutzsignal und Störsignal bestimmt wird. | ||
*Der „Durchlassbereich” liegt vorwiegend bei den Frequenzen, bei denen das Nutzsignal sehr viel größere Anteile besitzt als die Störung: ${\it Φ}_s(f) >> {\it Φ}_n(f).$ | *Der „Durchlassbereich” liegt vorwiegend bei den Frequenzen, bei denen das Nutzsignal sehr viel größere Anteile besitzt als die Störung: ${\it Φ}_s(f) >> {\it Φ}_n(f).$ | ||
*Der mittlere quadratische Fehler (MQF) zwischen dem Filterausgangssignal $d(t)$ und dem zu approximierenden Eingangssignal $s(t)$ ist | *Der mittlere quadratische Fehler (MQF) zwischen dem Filterausgangssignal $d(t)$ und dem zu approximierenden Eingangssignal $s(t)$ ist | ||
| − | $${\rm MQF} = \int\limits_{ - \infty }^{ + \infty } {\frac{{ {\it \Phi }_s (f) \cdot {\it \Phi }_n (f)}}{{ {\it \Phi }_s(f) + {\it \Phi }_n (f)}}\,{\rm{d}}f = \int\limits_{ - \infty }^{ + \infty } {H_{\rm WF} (f) \cdot {\it \Phi }_n (f)}\, {\rm{d}}f.}$$ | + | :$${\rm MQF} = \int\limits_{ - \infty }^{ + \infty } {\frac{{ {\it \Phi }_s (f) \cdot {\it \Phi }_n (f)}}{{ {\it \Phi }_s(f) + {\it \Phi }_n (f)}}\,{\rm{d}}f = \int\limits_{ - \infty }^{ + \infty } {H_{\rm WF} (f) \cdot {\it \Phi }_n (f)}\, {\rm{d}}f.}$$ |
| − | Die | + | Die Herleitung dieser Ergebnisse ist durchaus nicht trivial und zum Beispiel in [Hän97]<ref>Hänsler, E.: ''Statistische Signale: Grundlagen und Anwendungen.'' 2. Auflage. Berlin – Heidelberg: Springer, 1997.</ref> zu finden. In den beiden nächsten Abschnitten wird das Wiener–Kolmogorow–Filter anhand zweier Beispiele verdeutlicht. |
| − | ==Interpretation des Wiener-Filters | + | ==Interpretation des Wiener-Filters== |
{{Beispiel}} | {{Beispiel}} | ||
'''1)''' Zur Verdeutlichung des Wiener–Filters betrachten wir zunächst als Grenzfall ein Sendesignal $s(t)$ mit dem LDS ${\it Φ}_s(f) = P_s · δ(f ± f_s).$ | '''1)''' Zur Verdeutlichung des Wiener–Filters betrachten wir zunächst als Grenzfall ein Sendesignal $s(t)$ mit dem LDS ${\it Φ}_s(f) = P_s · δ(f ± f_s).$ | ||
| Zeile 64: | Zeile 61: | ||
Dieses Beispiel hat einen Sonderfall behandelt, bei dem das bestmögliche Ergebnis MQF = 0 zumindest theoretisch möglich ist. Das folgende Beispiel geht von realistischeren Annahmen aus und liefert das Ergebnis MQF >0. | Dieses Beispiel hat einen Sonderfall behandelt, bei dem das bestmögliche Ergebnis MQF = 0 zumindest theoretisch möglich ist. Das folgende Beispiel geht von realistischeren Annahmen aus und liefert das Ergebnis MQF >0. | ||
| − | |||
{{Beispiel}} | {{Beispiel}} | ||
'''2)''' Nun betrachten wir ein ''stochastisches rechteckförmiges Binärsignal'' $s(t)$, das durch weißes Rauschen $n(t)$ additiv überlagert ist. Die Grafik enthält folgende Diagramme: | '''2)''' Nun betrachten wir ein ''stochastisches rechteckförmiges Binärsignal'' $s(t)$, das durch weißes Rauschen $n(t)$ additiv überlagert ist. Die Grafik enthält folgende Diagramme: | ||
Version vom 24. April 2017, 12:19 Uhr
Inhaltsverzeichnis
Optimierungskriterium des Wiener–Kolmogorow–Filters
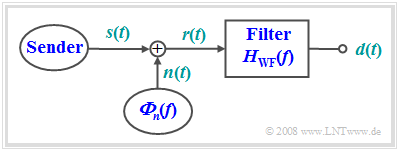
Als weiteres Beispiel zur Optimalfilterung betrachten wir nun die Aufgabenstellung, die Form eines Nutzsignals $s(t)$ aus dem durch additives Rauschen $n(t)$ gestörten Empfangssignals $r(t)$ im Sinne des mittleren quadratischen Fehlers (MQF) möglichst gut zu rekonstruieren: $${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t} \mathop = \limits^! {\rm{Minimum}}.$$
Das entsprechende Filter ist nach seinen Erfindern Norbert Wiener und Andrei Nikolajewitsch Kolmogorow benannt. Den entsprechenden Frequenzgang bezeichnen wir mit $H_{\rm WF}(f).$
Für diese Optimierungsaufgabe gelten folgende Voraussetzungen:
- Das zu rekonstruierende Signal $s(t)$ ist das Ergebnis eines Zufallsprozesses { $s(t)$}, von dem nur die statistischen Eigenschaften in Form des Leistungsdichtespektrums ${\it Φ}_s(f)$ bekannt ist.
- Das Störsignal $n(t)$ ist durch das LDS ${\it Φ}_n(f)$ gegeben. Korrelationen zwischen dem Nutz– und dem Störsignal berücksichtigen die Kreuzleistungsdichtespektren ${\it Φ}_{sn}(f) = \hspace{0.1cm} –{ {\it Φ}_{ns} }^∗(f).$
- Das Ausgangssignal des gesuchten Filters ist mit $d(t)$ bezeichnet, das sich entsprechend des MQF möglichst wenig von $d(t)$ unterscheiden soll. $T_{\rm M}$ bezeichnet wiederum die Messdauer.
Das Signal $s(t)$ sei mittelwertfrei $(m_s = 0)$ und leistungsbegrenzt. Das bedeutet: Die Signalenergie $E_s$ ist aufgrund der unendlichen Ausdehnung des Signals $s(t)$ unendlich und die Signalleistung besitzt einen endlichen Wert:
- $$P_s = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {s(t)^2 \, {\rm{d}}t > 0.}$$
Ein grundsätzlicher Unterschied zur Aufgabenstellung beim Matched–Filter ist das stochastische und leistungsbegrenzte Nutzsignal $s(t)$. Erinnern wir uns: Beim Matched–Filter war das zu rekonstruierende Signal $g(t)$ deterministisch, zeitlich begrenzt und damit auch energiebegrenzt.
Ergebnis der Filteroptimierung
A. Kolmogorow und N. Wiener haben dieses Optimierungsproblem nahezu zur gleichen Zeit unabhängig voneinander gelöst. Die Übertragungsfunktion des optimalen Filters kann über die so genannte Wiener-Hopfsche Integralgleichung ermittelt werden, und lautet:
- $$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) + {\it \Phi }_{ns} (f)} }{ { {\it \Phi }_s (f) + {\it \Phi }_{sn} (f) + {\it \Phi }_{ns} (f) + {\it \Phi }_n (f)}}.$$
Der Index „WF” steht für Wiener-Filter und lässt leider die Verdienste von Kolmogorow nicht erkennen. Auf die exakte, mathematische Ableitung der Gleichung wird hier verzichtet. Vielmehr soll dieses Filter im Folgenden an einigen Sonderfällen verdeutlicht und interpretiert werden.
- Sind Signal und Störung unkorreliert ⇒ ${\it Φ}_{sn}(f) = {\it Φ}_{ns}(f) =$ 0, so vereinfacht sich die obige Gleichung wie folgt:
- $$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) }}{{ {\it \Phi }_s (f) + {\it \Phi }_n (f) }} = \frac{1}{{1 + {\it \Phi }_n (f) / {\it \Phi }_s (f) }}.$$
- Das Filter wirkt dann wie ein frequenzabhängiger Teiler, wobei das Teilerverhältnis durch die Leistungsdichtespektren von Nutzsignal und Störsignal bestimmt wird.
- Der „Durchlassbereich” liegt vorwiegend bei den Frequenzen, bei denen das Nutzsignal sehr viel größere Anteile besitzt als die Störung: ${\it Φ}_s(f) >> {\it Φ}_n(f).$
- Der mittlere quadratische Fehler (MQF) zwischen dem Filterausgangssignal $d(t)$ und dem zu approximierenden Eingangssignal $s(t)$ ist
- $${\rm MQF} = \int\limits_{ - \infty }^{ + \infty } {\frac{{ {\it \Phi }_s (f) \cdot {\it \Phi }_n (f)}}{{ {\it \Phi }_s(f) + {\it \Phi }_n (f)}}\,{\rm{d}}f = \int\limits_{ - \infty }^{ + \infty } {H_{\rm WF} (f) \cdot {\it \Phi }_n (f)}\, {\rm{d}}f.}$$
Die Herleitung dieser Ergebnisse ist durchaus nicht trivial und zum Beispiel in [Hän97][1] zu finden. In den beiden nächsten Abschnitten wird das Wiener–Kolmogorow–Filter anhand zweier Beispiele verdeutlicht.
Interpretation des Wiener-Filters
1) Zur Verdeutlichung des Wiener–Filters betrachten wir zunächst als Grenzfall ein Sendesignal $s(t)$ mit dem LDS ${\it Φ}_s(f) = P_s · δ(f ± f_s).$
- Damit ist bekannt, dass $s(t)$ eine harmonische Schwingung mit der Frequenz $f_s$ ist.
- Unbekannt sind dagegen Amplitude und Phase der aktuellen Musterfunktion $s(t)$.
Bei weißem Rauschen ⇒ ${\it Φ}_n(f) = N_0/2$ – lautet somit der Frequenzgang des Wiener-Filters:
$$H_{\rm WF} (f) = \frac{1}{{1 +({N_0 /2})/{( P_s \cdot\delta ( {f \pm f_s } )}})}.$$
- Bei allen Frequenzen mit Ausnahme von $f = ±f_s$ ergibt sich $H_{\rm WF}(f) =$ 0, da hier der Nenner unendlich groß wird.
- Berücksichtigt man weiter, dass $δ(f = ±f_s)$ an der Stelle $f = ±f_s$ unendlich groß ist, so erhält man weiter $H_{\rm MF}(f = ±f_s ) =$ 1.
- Das optimale Filter ist somit ein Bandpass um $f_s$ mit unendlich kleiner Bandbreite. Der mittlere quadratische Fehler zwischen dem Sendesignal $s(t)$ und dem Filterausgangssignal $d(t)$ beträgt
$${\rm{MQF}} = \int_{ - \infty }^{ + \infty } {H_{\rm WF} (f) \cdot {\it \Phi_n} (f) \,{\rm{d}}f = \mathop {\lim }\limits_{\varepsilon \hspace{0.03cm} {\rm > \hspace{0.03cm}0,}\;\;\varepsilon \hspace{0.03cm} \to \hspace{0.03cm}\rm 0 } }\hspace{0.1cm} \int_{f_s - \varepsilon }^{f_s + \varepsilon }\hspace{-0.3cm} {N_0 }\,\,{\rm{d}}f = 0.$$
- Dieses unendlich schmale Bandpass–Filter würde bei den getroffenen Voraussetzungen die vollständige Regenerierung der Harmonischen hinsichtlich Amplitude und Phase erlauben. Unabhängig von der Größe der Störung $(N_0)$ würde somit $d(t) = s(t)$ gelten.
- Allerdings ist ein unendlich schmales Filter nicht realisierbar. Bei endlicher Bandbreite $Δf$ ist der mittlere quadratische Fehler (MQF) gleich $N_0 · Δf$.
Dieses Beispiel hat einen Sonderfall behandelt, bei dem das bestmögliche Ergebnis MQF = 0 zumindest theoretisch möglich ist. Das folgende Beispiel geht von realistischeren Annahmen aus und liefert das Ergebnis MQF >0.
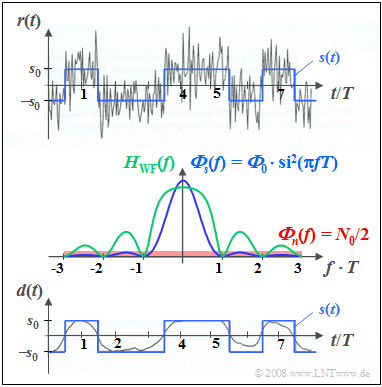
2) Nun betrachten wir ein stochastisches rechteckförmiges Binärsignal $s(t)$, das durch weißes Rauschen $n(t)$ additiv überlagert ist. Die Grafik enthält folgende Diagramme:
- Oben ist in grauer Farbe das Summensignal $r(t) = s(t) + n(t)$ für ${\it Φ}_0/N_0 =$ 5 dargestellt, wobei ${\it Φ}_0$ gleich der Energie eines Einzelimpulses ist und $N_0$ die Rauschleistungsdichte des weißen Rauschens angibt.
- In Bildmitte sind die Leistungsdichtespektren ${\it Φ}_s(f)$ und ${\it Φ}_n(f)$ in blauer bzw. roter Farbe skizziert und formelmäßig angegeben. Grün gezeichnet ist der Frequenzgang $H_{\rm WF}(f)$.
- Das untere Bild zeigt als grauen Kurvenzug das Ausgangssignal $d(t)$ des Wiener-Filters im Vergleich zum blau gezeichneten Signal $s(t)$. Im Idealfall sollte $d(t) = s(t)$ gelten.
Die untere Darstellung zeigt:
1. Der mittlere quadratische Fehler (MQF) zwischen den Signalen $d(t)$ und $s(t)$ beträgt hier etwa 11% der Nutzleistung $P_s$.
2. Im Signal $d(t)$ fehlen vorwiegend die höherfrequenten Signalanteile (also die Sprünge).
3. Diese Anteile werden zugunsten einer besseren Störunterdrückung bei diesen Frequenzen ausgefiltert.
Mit keinem anderen Filter ergibt sich bei diesen Voraussetzungen ein kleinerer (mittlerer quadratischer) Fehler als mit dem Wiener-Filter. Dessen Frequenzgang lautet hier: $$H_{\rm WF} (f) = \frac{1}{{1 + ({N_0 /2})/( {\it \Phi}_0 \cdot {\rm si^2} ( \pi f T )})} \hspace{0.15cm} .$$
Man erkennt aus dem mittleren Diagramm:
- Der Gleichsignalübertragungsfaktor ergibt sich zu $H_{\rm WF}(f = 0) = {\it Φ}_0/({\it Φ}_0 + N_0/2) = 10/11.$
- Bei Vielfachen der Symbolfolgefrequenz $1/T$, bei denen das stochastische Binärsignal $s(t)$ keine Spektralanteile besitzt, ist auch $H_{\rm WF}(f) =$ 0.
- Je mehr Nutzsignalanteile bei einer bestimmten Frequenz vorhanden sind, desto durchlässiger ist bei dieser Frequenz auch das Wiener-Filter.
Quellenverzeichnis
- ↑ Hänsler, E.: Statistische Signale: Grundlagen und Anwendungen. 2. Auflage. Berlin – Heidelberg: Springer, 1997.