Informationstheorie/Gedächtnislose Nachrichtenquellen

1. Informationstheorie
2. Entropie wertdiskreter Nachrichtenquellen
3. Gedächtnislose Nachrichtenquellen

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Dieses erste Kapitel beschreibt die Berechnung und die Bedeutung der Entropie. Diese ist entsprechend der Shannonshen Informationsdefinition ein Maß für die mittlere Unsicherheit über den Ausgang eines statistischen Ereignisses oder die Unsicherheit bei der Messung einer stochastischen Größe. Etwas salopp ausgedrückt quantifiziert die Entropie einer Zufallsgröße deren „Zufälligkeit”.

Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im Versuch „Wertdiskrete Informationstheorie” des Praktikums „Simulation Digitaler Übertragungssysteme ”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf

• dem Windows-Programm WDIT  ⇒  Link verweist auf die ZIP-Version des Programms; und
• der zugehörigen Praktikumsanleitung  ⇒  Link verweist auf die PDF-Version.

Der erste Abschnitt „Gedächtnislose Nachrichtenquellen” ist wie folgt gegliedert:

Modell und Voraussetzungen

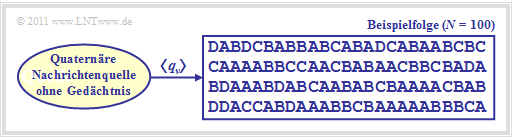
Wir betrachten eine wertdiskrete Nachrichtenquelle $\rm Q$, die eine Folge $ \langle q_ν \rangle$ von Symbolen abgibt.

• Für die Laufvariable gilt $ν = 1$, ... , $N$, wobei $N$ „hinreichend groß” sein sollte.
• Jedes einzelne Quellensymbol $q_ν$ entstammt einem Symbolvorrat $\{q_μ \}$ mit $μ = 1$, ... , $M$, wobei $M$ den Symbolumfang bezeichnet:

$$q_{\nu} \in \left \{ q_{\mu} \right \}, \hspace{0.15cm}{\rm mit}\hspace{0.15cm} \nu = 1, ... \hspace{0.05cm}, N\hspace{0.15cm}{\rm und}\hspace{0.15cm}\mu = 1, ...\hspace{0.05cm} , M \hspace{0.05cm}.$$

Die Grafik zeigt eine quaternäre Nachrichtenquelle $(M = 4)$ mit dem Alphabet $\rm \{A, B, C, D\}$ und eine beispielhafte Folge der Länge $N = 100$.

Es gelten folgende Voraussetzungen:

• Die quaternäre Nachrichtenquelle wird durch $M = 4$ Symbolwahrscheinlichkeiten $p_μ$ vollständig beschrieben. Allgemein gilt:

$$\sum_{\mu = 1}^M \hspace{0.1cm}p_{\mu} = 1 \hspace{0.05cm}.$$

• Die Nachrichtenquelle sei gedächtnislos, das heißt, die einzelnen Folgenelemente seien statistisch voneinander unabhängig:

$${\rm Pr} \left (q_{\nu} = q_{\mu} \right ) = {\rm Pr} \left (q_{\nu} = q_{\mu} \hspace{0.03cm} | \hspace{0.03cm} q_{\nu -1}, q_{\nu -2}, ... \right ) \hspace{0.05cm}.$$

• Da das Alphabet aus Symbolen (und nicht aus Zufallsgrößen) besteht, ist hier die Angabe von Erwartungswerten (linearer Mittelwert, quadratischer Mittelwert, Streuung, usw.) nicht möglich, aus informationstheoretischer Sicht aber auch nicht nötig.

Diese Eigenschaften werden nun mit einem Beispiel verdeutlicht.

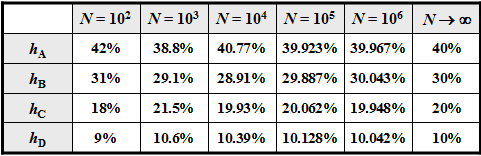
Beispiel:  Für die Symbolwahrscheinlichkeiten einer Quaternärquelle gelte:

$$p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.1\hspace{0.05cm}.$$

Bei einer unendlich langen Folge $(N \to \infty)$ wären die relativen Häufigkeiten $h_{\rm A}$, $h_{\rm B}$, $h_{\rm C}$ und $h_{\rm D}$ – also die a–posteriori–Kenngrößen – identisch mit den a–priori–Wahrscheinlichkeiten $p_{\rm A}$, $p_{\rm B}$, $p_{\rm C}$ und $p_{\rm D}$. Bei kleinerem $N$ kann es aber durchaus zu Abweichungen kommen, wie die folgende Tabelle (Ergebnis einer Simulation) zeigt. Eine beispielhafte Folge mit $N = 100$ Symbolen ist ist in der oberen Grafik angegeben.

Aufgrund der Mengenelemente $\rm A$, $\rm B$, $\rm C$ und $\rm D$ können keine Mittelwerte angegeben werden. Ersetzt man die Symbole durch Zahlenwerte, zum Beispiel $\rm A \Rightarrow 1$, $\rm B \Rightarrow 2$, $\rm C \Rightarrow 3$, $\rm D \Rightarrow 4$, so ergeben sich

• für den linearen Mittelwert:

$$m_1 = {\rm E} \left [ q_{\nu} \right ] = {\rm E} \left [ q_{\mu} \right ] = 0.4 \cdot 1 + 0.3 \cdot 2 + 0.2 \cdot 3 + 0.1 \cdot 4 = 2 \hspace{0.05cm},$$

• für den quadratischen Mittelwert:

$$m_2 = {\rm E} \left [ q_{\nu}^{\hspace{0.05cm}2} \right ] = {\rm E} \left [ q_{\mu}^{\hspace{0.05cm}2} \right ] = 0.4 \cdot 1^2 + 0.3 \cdot 2^2 + 0.2 \cdot 3^2 + 0.1 \cdot 4^2 = 5 \hspace{0.05cm},$$

• für die Standardabweichung (Streuung) nach dem „Satz von Steiner”:

$$\sigma = \sqrt {m_2 - m_1^{\hspace{0.05cm}2}} = \sqrt {5 - 2^{\hspace{0.01cm}2}} = 1 \hspace{0.05cm}.$$

Entscheidungsgehalt – Nachrichtengehalt

Claude Elwood Shannon definierte 1948 im Standardwerk der Informationstheorie [Sha48] den Informationsbegriff als „Abnahme der Ungewissheit über das Eintreten eines statistischen Ereignisses”. Machen wir hierzu ein gedankliches Experiment mit M möglichen Ergebnissen, die alle gleichwahrscheinlich seien:

$$p_1 = p_2 = ... = p_M = 1/M \hspace{0.05cm}.$$

Unter dieser Annahme gilt:

• Ist $M$ = 1, so wird jeder einzelne Versuch das gleiche Ergebnis liefern und demzufolge besteht keine Unsicherheit hinsichtlich des Ausgangs. Wird uns das Versuchsergebnis mitgeteilt, so haben wir dadurch natürlich auch keinen Informationsgewinn.
• Dagegen erfährt ein Beobachter bei einem Experiment mit $M$ = 2, zum Beispiel dem „Münzwurf” mit der Ereignismenge { Z(ahl), W(app) } und den Wahrscheinlichkeiten $p_Z$ = $p_W$ = 0.5, durchaus einen Informationsgewinn. Die Unsicherheit, ob Z oder W geworfen wurde, wird aufgelöst.
• Beim Experiment „Würfeln” ( $M$ = 6 ) und noch mehr beim Roulette ( $M$ = 37) ist die gewonnene Information für den Beobachter noch deutlich größer als beim „Münzwurf”, wenn er erfährt, welche Zahl gewürfelt bzw. welche Kugel gefallen ist.
• Schließlich sollte noch berücksichtigt werden, dass das Experiment „Dreifacher Münzwurf” mit den $M$ = 8 möglichen Ergebnissen ZZZ, ZZW, ZWZ, ZWW, WZZ, WZW, WWZ, WWW die dreifache Information liefert wie der einfache Münzwurf ( $M$ = 2 ).

Die nachfolgende Festlegung erfüllt alle hier verbal aufgeführten Anforderungen an ein quantitatives Informationsmaß bei gleichwahrscheinlichen Ereignissen, gekennzeichnet durch den Symbolumfang $M$.

Der Entscheidungsgehalt einer Nachrichtenquelle hängt nur vom Symbolumfang $M$ ab und ergibt sich zu

$$H_0 = {\rm log}\hspace{0.1cm}M = {\rm log}_2\hspace{0.1cm}M \hspace{0.15cm}{\rm (in \hspace{0.15cm}"bit")} = {\rm ln}\hspace{0.1cm}M \hspace{0.15cm}{\rm (in \hspace{0.15cm}"nat")} = {\rm lg}\hspace{0.1cm}M \hspace{0.15cm}{\rm (in \hspace{0.15cm}"Hartley")} \hspace{0.05cm}.$$

Gebräuchlich ist hierfür auch die Bezeichnung Nachrichtengehalt. Da $H_0$ gleichzeitig den Maximalwert der Entropie $H$ angibt, wird in hier teilweise auch $H_\text{max}$ als Kurzzeichen verwendet.

Anzumerken ist:

• Der Logarithmus wird in unserem Tutorial unabhängig von der Basis mit „log” bezeichnet. Die vier oben aufgestellten Kriterien werden aufgrund folgender Eigenschaften erfüllt:

$${\rm log}\hspace{0.1cm}1 = 0 \hspace{0.05cm},\hspace{0.2cm} {\rm log}\hspace{0.1cm}37 > {\rm log}\hspace{0.1cm}6 > {\rm log}\hspace{0.1cm}2\hspace{0.05cm},\hspace{0.2cm} {\rm log}\hspace{0.1cm}M^k = k \cdot {\rm log}\hspace{0.1cm}M \hspace{0.05cm}.$$

• Meist verwenden wir den Logarithmus zur Basis 2 ⇒ Logarithmus dualis (ld), wobei dann die Pseudoeinheit „bit” – genauer: „bit/Symbol” – hinzugefügt wird:

$${\rm ld}\hspace{0.1cm}M = {\rm log_2}\hspace{0.1cm}M = \frac{{\rm lg}\hspace{0.1cm}M}{{\rm lg}\hspace{0.1cm}2} = \frac{{\rm ln}\hspace{0.1cm}M}{{\rm ln}\hspace{0.1cm}2} \hspace{0.05cm}.$$

• Weiter findet man in der Literatur auch Definitionen, basierend auf dem natürlichen Logarithmus („ln”) oder dem Zehnerlogarithmus („lg”) entsprechend obigen Definitionen.

Informationsgehalt und Entropie

Wir verzichten nun auf die bisherige Voraussetzung, dass alle $M$ möglichen Ergebnisse eines Versuchs gleichwahrscheinlich seien. Im Hinblick auf eine möglichst kompakte Schreibweise legen wir für diese Seite lediglich fest:

$$p_1 > p_2 > ... > p_\mu > ... > p_{M-1} > p_M\hspace{0.05cm},\hspace{0.4cm}\sum_{\mu = 1}^M p_{\mu} = 1 \hspace{0.05cm}.$$

Unter dieser Voraussetzung betrachten wir nun den Informationsgehalt der einzelnen Symbole, wobei wir den Logarithmus dualis mit „ld”(manchmal auch mit „log2”) bezeichnen :

$$I_\mu = {\rm ld}\hspace{0.1cm}\frac{1}{p_\mu}= -\hspace{0.05cm}{\rm ld}\hspace{0.1cm}{p_\mu} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$

Man erkennt:

• Wegen $p_μ$ ≤ 1 ist der Informationsgehalt nie negativ. Im Grenzfall $p_μ$ → 1 geht $I_μ$ → 0. Allerdings ist für $I_μ$ = 0 → $p_μ$ = 1 → $M$ = 1 auch der Entscheidungsgehalt $H_0$ = 0.
• Bei abfallenden Wahrscheinlichkeiten $p_μ$ nimmt der Informationsgehalt kontinuierlich zu:

$$I_1 < I_2 < ... < I_\mu < ... < I_{M-1} < I_M \hspace{0.05cm}.$$

Das heißt: Je weniger wahrscheinlich ein Ereignis ist, desto größer ist sein Informationsgehalt. Dieser Sachverhalt ist auch im täglichen Leben festzustellen:

• „6 Richtige” im Lotto nimmt man sicher eher war als „3 Richtige” oder gar keinen Gewinn.
• Ein Tsunami in Asien dominiert auch die Nachrichten in Deutschland über Wochen im Gegensatz zu den fast standardmäßigen Verspätungen der Deutschen Bahn.
• Eine Niederlagenserie von Bayern München führt zu Riesen–Schlagzeilen im Gegensatz zu einer Siegesserie. Bei 1860 München ist genau das Gegenteil der Fall.

Der Informationsgehalt eines einzelnen Symbols (oder Ereignisses) ist allerdings nicht sehr interessant. Durch Scharmittelung über alle möglichen Symbole $q_μ$ bzw. durch Zeitmittelung über alle Folgenelemente $q_ν$ erhält man dagegen eine der zentralen Größen der Informationstheorie.

Die Entropie einer Quelle gibt den mittleren Informationsgehalt aller Symbole an:

$$H = \overline{I_\nu} = {\rm E}\hspace{0.01cm}[I_\mu] = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm ld}\hspace{0.1cm}\frac{1}{p_\mu}= -\sum_{\mu = 1}^M p_{\mu} \cdot{\rm ld}\hspace{0.1cm}{p_\mu} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit[/Symbol])} \hspace{0.05cm}.$$

Die überstreichende Linie kennzeichnet eine Zeitmittelung und E[...] eine Scharmittelung.

Die Entropie ist ein Maß für

• die mittlere Unsicherheit über den Ausgang eines statistischen Ereignisses,
• die „Zufälligkeit” dieses Ereignisses,
• den mittleren Informationsgehalt einer Zufallsgröße.

Binäre Entropiefunktion

Wir beschränken uns zunächst auf den Sonderfall $M$ = 2 und betrachten eine binäre Quelle, die die beiden Symbole A und B abgibt. Die Auftrittwahrscheinlichkeiten seien $p_A$ = $p$ und $p_B$ = 1 – $p$. Für die Entropie dieser Quelle gilt:

$$H_{\rm bin} (p) = p \cdot {\rm ld}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ld}\hspace{0.1cm}\frac{1}{1-p} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$

Man nennt diese Funktion $H_\text{bin}(p)$ die binäre Entropiefunktion. Die Entropie einer Quelle mit größerem Symbolumfang $M$ lässt sich häufig unter Verwendung von $H_\text{bin}(p)$ ausdrücken.

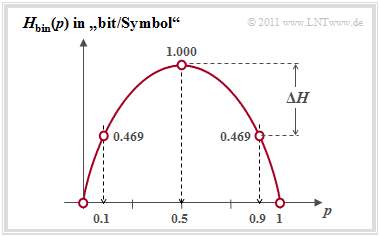
Die Grafik zeigt die Funktion $H_\text{bin}(p)$ für die Werte 0 ≤ $p$ ≤ 1 der Symbolwahrscheinlichkeit von A (oder B). Man erkennt:

• Der Maximalwert $H_\text{max}$ = 1 bit ergibt sich für $p$ = 0.5, also für gleichwahrscheinliche Binärsymbole. Dann liefern A und B jeweils den gleichen Beitrag zur Entropie.
• $H_\text{bin}(p)$ ist symmetrisch um $p$ = 0.5. Eine Quelle mit $p_A$ = 0.1 und $p_B$ = 0.9 hat die gleiche Entropie (Zufälligkeit) $H$ = 0.469 bit wie eine Quelle mit $p_A$ = 0.9 und $p_B$ = 0.1.
• Die Differenz $ΔH$ = $H_\text{max}$ – $H$ gibt die Redundanz der Quelle an und $r$ = $ΔH/H_\text{max}$ die relative Redundanz. Im genannten Beispiel ergeben sich $ΔH$ = 0.531 bit bzw. $r$ = 53.1%.
• Für $p$ = 0 ergibt sich $H$ = 0, da hier die Ausgangsfolge „B B B ...” sicher vorhersagbar ist. Eigentlich beträgt nun der Symbolumfang nur noch $M$ = 1. Gleiches gilt für $p$ = 1.

Es sollte noch erwähnt werden, dass die binäre Entropiefunktion konkav ist, da deren zweite Ableitung nach dem Parameter $p$ für alle Werte von $p$ negativ ist:

$$\frac{{\rm d}^2H_{\rm bin} (p)}{{\rm d}\,p^2} = \frac{-1}{{\rm ln}(2) \cdot p \cdot (1-p)}< 0 \hspace{0.05cm}.$$

Nachrichtenquellen mit größerem Symbolumfang

Im ersten Abschnitt dieses Kapitels haben wir eine quaternäre Nachrichtenquelle ($M$ = 4) mit den Symbolwahrscheinlichkeiten $p_A$ = 0.4, $p_B$ = 0.3, $p_C$ = 0.2 und $p_D$ = 0.1 betrachtet. Diese besitzt die folgende Entropie:

$$\begin{align*}H_{\rm quat} \hspace{-0.1cm} & = \hspace{-0.1cm} 0.4 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.4} + 0.3 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.2}+ 0.1 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.1}=\\ \hspace{-0.1cm} & = \hspace{-0.1cm}\frac{1}{{\rm lg}\hspace{0.1cm}2} \cdot \left [ 0.4 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.4} + 0.3 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.3} + 0.2 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.2}+ 0.1 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.1} \right ] = 1.845\,{\rm bit} \hspace{0.05cm}.\end{align*}$$

Oft ist der Umweg über den Zehnerlogarithmus lg $x$ = log10 $x$ sinnvoll, da meist der Logarithmus dualis log2 $x$ (oder auch ld $x$) auf Taschenrechnern nicht zu finden ist. Bestehen zwischen den einzelnen Symbolwahrscheinlichkeiten Symmetrien wie im Beispiel

$$p_{\rm A} = p_{\rm D} = p \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = p_{\rm C} = 0.5-p \hspace{0.05cm},\hspace{0.3cm}{\rm mit} \hspace{0.15cm}0 \le p \le 0.5 \hspace{0.05cm},$$

so kann zur Entropieberechnung auf die binäre Entropiefunktion zurückgegriffen werden:

$$H_{\rm quat} = 2 \cdot p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + 2 \cdot (0.5-p) \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.5-p} = 1 + H_{\rm bin}(2p) \hspace{0.05cm}.$$

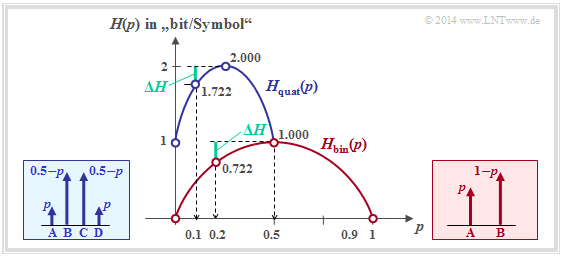
Die Grafik zeigt den Entropieverlauf der Quaternärquelle (blau) im Vergleich zur Binärquelle (rot) abhängig von $p$. Für die Quaternärquelle ist nur der Abszissenbereich 0 ≤ $p$ ≤ 0.5 zulässig.

Man erkennt aus der blauen Kurve für die Quaternärquelle:

• Die maximale Entropie $H_\text{max}$ = 2 bit ergibt sich für $p$ = 0.25 ⇒ $p_A$ = $p_B$ = $p_C$ = $p_D$ = 0.25, also wieder für gleichwahrscheinliche Symbole.
• Mit $p$ = 0 bzw. $p$ = 0.5 entartet die Quaternärquelle zu einer Binärquelle mit $p_B$ = $p_C$ = 0.5 bzw. $p_A$ = $p_D$ = 0.5. In diesem Fall ergibt sich die Entropie zu $H$ = 1 bit.
• Die Quelle mit $p_A$ = $p_D$ = $p$ = 0.1 und $p_B$ = $p_C$ = 0.4 weist folgende Entropie und (relative) Redundanz auf:

$$\begin{align*}H \hspace{-0.1cm} & = \hspace{-0.1cm} 1 + H_{\rm bin} (2p) =1 + H_{\rm bin} (0.2) = 1.722\,{\rm bit}\hspace{0.05cm},\\ {\rm \Delta }H \hspace{-0.1cm} & = \hspace{-0.1cm} {\rm ld}\hspace{0.1cm} M - H =2\,{\rm bit}- 1.722\,{\rm bit} = 0.278\,{\rm bit}\hspace{0.05cm},\\ r \hspace{-0.1cm} & = \hspace{-0.1cm} {\rm \Delta }H/({\rm ld}\hspace{0.1cm} M) = 0.139\hspace{0.05cm}.\end{align*}$$

Die Redundanz $ΔH$ der Quaternärquelle mit $p$ = 0.1 ist gleich 0.278 bit und damit genau so groß wie die Redundanz der Binärquelle mit $p$ = 0.2. Anmerkung: Als Pseudoeinheit ist hier stets „bit” angegeben. Genauer wäre „bit/Symbol”.