Aufgaben:Aufgabe 2.5: Restredundanz bei LZW-Codierung: Unterschied zwischen den Versionen
| Zeile 89: | Zeile 89: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Die Näherung <i>r' </i><sup> </sup>(<i>N</i>) stimmt definitionsgemäß für die Eingangsfolgenlänge <i>N</i> = 10000 mit der per Simulation ermittelten Restredundanz <i>r </i>(<i>N</i>) = 0.265 exakt überein. Damit ist | |
:$$A = 4 \cdot r(N = 10000) =4 \cdot {0.265} \hspace{0.15cm}\underline{= 1.06} | :$$A = 4 \cdot r(N = 10000) =4 \cdot {0.265} \hspace{0.15cm}\underline{= 1.06} | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | + | '''(2)''' Aus der Beziehung <i>A</i>/lg (<i>N</i>) ≤ 0.05 ⇒ <i>A</i>/lg (<i>N</i><sub>2</sub>) = 0.05 folgt: | |
| − | :$${{\rm lg}\hspace{0.1cm}N_{\rm | + | :$${{\rm lg}\hspace{0.1cm}N_{\rm 2}} = \frac{A}{0.05} = 21.2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} |
| − | N_{\rm | + | N_{\rm 2} = 10^{21.2} \hspace{0.15cm}\underline{= 1.58 \cdot 10^{21}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | '''(3)''' Allgemein gilt $r(N) = 1 - {H}/{K(N)} \hspace{0.05cm}.$ '''BQ1''' hat die Entropie <i>H</i> = 0.5 bit/Symbol. Daraus folgt wegen <i>r </i>(<i>N</i>) ≈ <i>r' </i><sup> </sup>(<i>N</i>) für <i>K</i>(<i>N</i><sub>3</sub>) = 0.6: | |
| − | |||
| − | \hspace{0.05cm}. $ | ||
| − | |||
:$$r(N_{\rm c}) = 1 - \frac{0.5}{0.6} = 0.167 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} | :$$r(N_{\rm c}) = 1 - \frac{0.5}{0.6} = 0.167 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} | ||
| − | {\rm lg}\hspace{0.1cm}N_{\rm | + | {\rm lg}\hspace{0.1cm}N_{\rm 3} = \frac{A}{0.167} = 6.36 |
\hspace{0.1cm}\Rightarrow\hspace{0.1cm} | \hspace{0.1cm}\Rightarrow\hspace{0.1cm} | ||
| − | N_{\rm | + | N_{\rm 3} = 10^{6.36} \hspace{0.15cm}\underline{= 2.29 \cdot 10^{6}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | : | + | [[Datei:P_ID2447__Inf_A_2_5d.png|right|Ergebnisse für die Quelle BQ2]] |
| + | '''(4)''' Für <i>N</i> = 10000 gilt <i>r' </i>(<i>N</i>) = <i>r</i>(<i>N</i>) = 0.19: | ||
:$$\frac{A}{{\rm lg}\hspace{0.1cm}10000} = 0.19 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | :$$\frac{A}{{\rm lg}\hspace{0.1cm}10000} = 0.19 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
A = 0.19 \cdot 4 = 0.76 \hspace{0.05cm}. $$ | A = 0.19 \cdot 4 = 0.76 \hspace{0.05cm}. $$ | ||
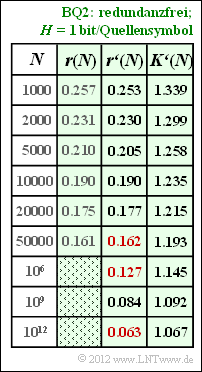
| − | + | Die Ergebnisse sind in nebenstehender Tabelle zusammengefasst. Man erkennt die sehr gute Übereinstimmung zwischen <i>r </i>(<i>N</i>) und <i>r' </i>(<i>N</i>). Die gesuchten Zahlenwerte sind in der Tabelle rot markiert: | |
| + | $$r'(N = 50000)\hspace{0.15cm}\underline{ = 0.162},\hspace{0.3cm}r'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.127},\hspace{0.3cm} | ||
| + | r'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.063}.$$ | ||
| − | + | Für den Komprimierungsfaktor gilt (der Apostroph weist darauf hin, dass von der Näherung <i>r'</i>(<i>N</i>) ausgegangen wurde): | |
:$$K'(N) = \frac{1}{1 - r'(N)}\hspace{0.05cm}.$$ | :$$K'(N) = \frac{1}{1 - r'(N)}\hspace{0.05cm}.$$ | ||
| − | + | Damit gilt für die Länge des LZW–Ausgabestrings: | |
| − | :$$L'(N) = K'(N) \cdot N \hspace{0.05cm}.$$ | + | :$$L'(N) = K'(N) \cdot N = \frac{N}{1 - r'(N)}\hspace{0.05cm}.$$ |
| − | : | + | [[Datei:P_ID2448__Inf_A_2_5e.png|right|Ergebnisse für die Quelle BQ3]] |
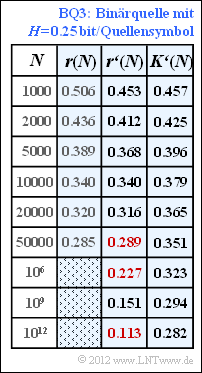
| − | + | '''(5)''' Nach ähnlicher Vorgehensweise wie in der Teilaufgabe (4) erhält man für die Binärquelle '''BQ3''' den Anpassungsparameter <i>A</i> = 1.36 und daraus die Ergebnisse gemäß der blau hinterlegten Tabelle. | |
| − | + | <u>Hinweis:</u> Die letzte Spalte dieser Tabelle ist nur bei Kenntnis der Teilaufgabe (6) verständlich. Dort wird gezeigt, dass die Quelle '''BQ3''' die Entropie <i>H</i> = 0.25 bit/Quellensymbol besitzt. | |
| − | + | In diesem Fall gilt für den Komprimierungsfaktor: | |
:$$K'(N) = \frac{H}{1 - r'(N)} = \frac{0.25}{1 - r'(N)} \hspace{0.05cm}.$$ | :$$K'(N) = \frac{H}{1 - r'(N)} = \frac{0.25}{1 - r'(N)} \hspace{0.05cm}.$$ | ||
| − | + | Damit erhält man für die gesuchten Werte der Restredundanz: | |
| − | + | $$r'(N = 50000)\hspace{0.15cm}\underline{ = 0.289},\hspace{0.3cm}r'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.227},\hspace{0.3cm} | |
| − | + | r'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.113}.$$ | |
| − | + | Für <i>N</i> = 10<sup>12</sup> weicht also der Komprimierungsfaktor (0.282) noch deutlich von der Entropie (0.25) ab, die für <i>N</i> → ∞ erreicht werden kann (Quellencodierungstheorem). | |
| − | |||
| − | :* Quelle BQ1 | + | '''(6)''' Die einzelnen Näherungen <i>r' </i>(<i>N</i>) unterscheiden sich nur durch den Parameter <i>A</i>. Dabei haben wir festgestellt: |
| + | * Quelle '''BQ1''' mit <i>H</i> = 0.50: <i>A</i> = 1.0 – entsprechend dem Angabenblatt), | ||
| + | * Quelle '''BQ2''' mit <i>H</i> = 1.00: <i>A</i> = 0.76 – siehe Teilaufgabe (4) | ||
| + | * Quelle BQ3 (<i>H</i> unbekannt): <i>A</i> = 4 · 0.341 =1.364 – entsprechend der letzten Spalte in der Tabelle. | ||
| − | |||
| − | + | Je kleiner die Entropie <i>H</i> ist, um so größer ist offensichtlich der Anpassungsfaktor <i>A</i> (und umgekehrt). <br> | |
| + | Da genau eine Lösung möglich ist, muss <i>H</i> = 0.25 bit/Quellensymbol richtig sein ⇒ <u>Antwort 4</u>. | ||
| − | + | Tatsächlich wurden bei der Simulation für die Quelle '''BQ3''' die Wahrscheinlichkeiten <i>p</i><sub>A</sub> = 0.96, <i>p</i><sub>B</sub> = 0.04 ⇒ <i>H</i> ≈ 0.25 verwendet. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 22. Mai 2017, 13:50 Uhr
Wir gehen hier von einer binären Eingangsfolge der Länge N aus und betrachten drei verschiedene binäre Nachrichtenquellen:
- BQ1: Symbolwahrscheinlichkeiten pA = 0.89, pB = 0.11, also unterschiedlich
⇒ Entropie H = 0.5 bit/Quellensymbol ⇒ Quelle ist redundant. - BQ2: pA = pB = 0.5 (gleichwahrscheinlich) ⇒ Entropie H = 1 bit/Quellensymbol
⇒ Quelle ist redundanzfrei. - BQ3: Hier gibt es keine konkreten Angaben zur Statistik. In der Teilaufgabe (6) sollen Sie die Entropie H dieser Quelle abschätzen.
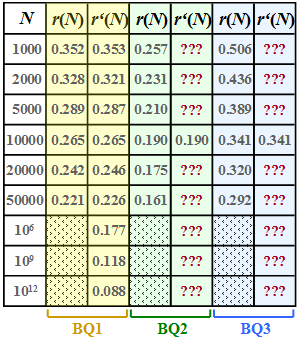
Für diese drei Quellen wurden per Simulation die jeweilige Restredundanz r(N) ermittelt, die nach der Lempel–Ziv–Welch–Codierung in der Binärfolge verbleibt. Die Ergebnisse sind in der jeweils ersten Spalte obiger Tabelle für die Quellen
- BQ1 (gelbe Hinterlegung),
- BQ2 (grüne Hinterlegung) und
- BQ3 (blaue Hinterlegung)
eingetragen, wobei wir uns bei der Simulation auf Folgenlängen N ≤ 50000 beschränkt haben.
Die relative Redundanz der Ausgangsfolge – vereinfachend Restredundanz genannt – kann aus
- der Länge N der Eingangsfolge,
- der Länge L(N) der Ausgangsfolge und
- der Quellenentropie H
in folgender Weise berechnet werden:
- $$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$
Hierbei ist berücksichtigt, dass bei perfekter Quellencodierung die Länge der Ausgangsfolge bis auf den Wert Lmin = N · H herabgesenkt werden könnte. Bei nichtperfekter Quellencodierung gibt L(N) – N · H die verbleibende Redundanz (mit der Pseudo–Einheit „bit”) an. Nach Division durch L(N) erhält man die relative Redundanz r (N) mit dem Wertebereich zwischen 0 und 1; r (N) sollte möglichst klein sein.
Eine zweite Kenngröße zur Effizienzmessung der LZW–Codierung ist der Komprimierungsfaktor K(N), der ebenfalls klein sein sollte:
- $$K(N) = {L(N) }/{N} \hspace{0.05cm},$$
Im Theorieteil wurde gezeigt, dass die Restredundanz r(N) oft durch die Funktion
- $$r'(N) ={A}/{{\rm lg}\hspace{0.1cm}(N)} \hspace{0.5cm}{\rm mit}\hspace{0.5cm} A = 4 \cdot {r(N = 10000)} \hspace{0.05cm}.$$
gut angenähert wird. Die Näherung r′(N) ist für BQ1 in der zweiten Spalte obiger Tabelle angegeben. In den Teilaufgaben (4) und (5) sollen Sie die Approximation für die Quellen BQ2 und BQ3 vornehmen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Komprimierung nach Lempel, Ziv und Welch.
- Insbesondere wird Bezug genommen auf die Seiten Restredrundanz als Maß für die Effizienz von Codierverfahren, Effizienz der Lempel-Ziv-Codierung sowie Quantitative Aussagen zur asymptotischen Optimalität.
- Die Beschreibungsgrößen K(N) und r(N) hängen deterministisch zusammen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$A = 4 \cdot r(N = 10000) =4 \cdot {0.265} \hspace{0.15cm}\underline{= 1.06} \hspace{0.05cm}. $$
(2) Aus der Beziehung A/lg (N) ≤ 0.05 ⇒ A/lg (N2) = 0.05 folgt:
- $${{\rm lg}\hspace{0.1cm}N_{\rm 2}} = \frac{A}{0.05} = 21.2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} N_{\rm 2} = 10^{21.2} \hspace{0.15cm}\underline{= 1.58 \cdot 10^{21}} \hspace{0.05cm}.$$
(3) Allgemein gilt $r(N) = 1 - {H}/{K(N)} \hspace{0.05cm}.$ BQ1 hat die Entropie H = 0.5 bit/Symbol. Daraus folgt wegen r (N) ≈ r' (N) für K(N3) = 0.6:
- $$r(N_{\rm c}) = 1 - \frac{0.5}{0.6} = 0.167 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} {\rm lg}\hspace{0.1cm}N_{\rm 3} = \frac{A}{0.167} = 6.36 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} N_{\rm 3} = 10^{6.36} \hspace{0.15cm}\underline{= 2.29 \cdot 10^{6}} \hspace{0.05cm}.$$
(4) Für N = 10000 gilt r' (N) = r(N) = 0.19:
- $$\frac{A}{{\rm lg}\hspace{0.1cm}10000} = 0.19 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.19 \cdot 4 = 0.76 \hspace{0.05cm}. $$
Die Ergebnisse sind in nebenstehender Tabelle zusammengefasst. Man erkennt die sehr gute Übereinstimmung zwischen r (N) und r' (N). Die gesuchten Zahlenwerte sind in der Tabelle rot markiert: $$r'(N = 50000)\hspace{0.15cm}\underline{ = 0.162},\hspace{0.3cm}r'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.127},\hspace{0.3cm} r'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.063}.$$
Für den Komprimierungsfaktor gilt (der Apostroph weist darauf hin, dass von der Näherung r'(N) ausgegangen wurde):
- $$K'(N) = \frac{1}{1 - r'(N)}\hspace{0.05cm}.$$
Damit gilt für die Länge des LZW–Ausgabestrings:
- $$L'(N) = K'(N) \cdot N = \frac{N}{1 - r'(N)}\hspace{0.05cm}.$$
(5) Nach ähnlicher Vorgehensweise wie in der Teilaufgabe (4) erhält man für die Binärquelle BQ3 den Anpassungsparameter A = 1.36 und daraus die Ergebnisse gemäß der blau hinterlegten Tabelle.
Hinweis: Die letzte Spalte dieser Tabelle ist nur bei Kenntnis der Teilaufgabe (6) verständlich. Dort wird gezeigt, dass die Quelle BQ3 die Entropie H = 0.25 bit/Quellensymbol besitzt.
In diesem Fall gilt für den Komprimierungsfaktor:
- $$K'(N) = \frac{H}{1 - r'(N)} = \frac{0.25}{1 - r'(N)} \hspace{0.05cm}.$$
Damit erhält man für die gesuchten Werte der Restredundanz: $$r'(N = 50000)\hspace{0.15cm}\underline{ = 0.289},\hspace{0.3cm}r'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.227},\hspace{0.3cm} r'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.113}.$$ Für N = 1012 weicht also der Komprimierungsfaktor (0.282) noch deutlich von der Entropie (0.25) ab, die für N → ∞ erreicht werden kann (Quellencodierungstheorem).
(6) Die einzelnen Näherungen r' (N) unterscheiden sich nur durch den Parameter A. Dabei haben wir festgestellt:
- Quelle BQ1 mit H = 0.50: A = 1.0 – entsprechend dem Angabenblatt),
- Quelle BQ2 mit H = 1.00: A = 0.76 – siehe Teilaufgabe (4)
- Quelle BQ3 (H unbekannt): A = 4 · 0.341 =1.364 – entsprechend der letzten Spalte in der Tabelle.
Je kleiner die Entropie H ist, um so größer ist offensichtlich der Anpassungsfaktor A (und umgekehrt).
Da genau eine Lösung möglich ist, muss H = 0.25 bit/Quellensymbol richtig sein ⇒ Antwort 4.
Tatsächlich wurden bei der Simulation für die Quelle BQ3 die Wahrscheinlichkeiten pA = 0.96, pB = 0.04 ⇒ H ≈ 0.25 verwendet.