Aufgaben:Aufgabe 2.7Z: Huffman-Codierung für Zweiertupel einer Ternärquelle: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 2.7Z Ternärquelle-Zweiertupel nach 2.7Z Huffman-Codierung für Zweiertupel einer Ternärquelle) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2458__Inf_Z_2_7.png|right|]] | + | [[Datei:P_ID2458__Inf_Z_2_7.png|right|Huffman–Baum für Ternärquelle]] |
| − | Wir betrachten den gleichen Sachverhalt wie in der Aufgabe A2.7: Der Huffman–Algorithmus führt zu einem besseren Ergebnis, das heißt zu einer kleineren mittleren Codewortlänge | + | Wir betrachten den gleichen Sachverhalt wie in der [[Aufgaben:2.7_Huffman-Anwendung_für_binäre_Zweiertupel|Aufgabe A2.7]]: Der Huffman–Algorithmus führt zu einem besseren Ergebnis, das heißt zu einer kleineren mittleren Codewortlänge $L_{\rm M}$, wenn man ihn nicht auf einzelne Symbole anwendet, sondern vorher $k$–Tupel bildet. Dadurch erhöht man den Symbolumfang von $M$ auf $M' = M^k$. |
Für die hier betrachtete Nachrichtenquelle gilt: | Für die hier betrachtete Nachrichtenquelle gilt: | ||
| + | * Symbolumfang: $M = 3$, | ||
| + | * Symbolvorrat: $\{$<b>X</b>, <b>Y</b>, <b>Z</b>$\}$, | ||
| + | * Wahrscheinlichkeiten: $p_{\rm X} = 0.7$, $p_{\rm Y} = 0.2$, $p_{\rm Z} = 0.1$, | ||
| + | * Entropie: $H = 1.157 \ \rm bit/Ternärsymbol$. | ||
| − | |||
| − | + | Die Grafik zeigt den Huffman–Baum, wenn man den Huffman–Algorithmus auf Einzelsymbole anwendet, also den Fall $k= 1$. In der Teilaufgabe (2) sollen Sie den entsprechenden Huffman–Code angeben, wenn vorher Zweiertupel gebildet werden ($k=2$). | |
| − | |||
| − | :* | + | ''Hinweise:'' |
| − | + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Entropiecodierung_nach_Huffman|Entropiecodierung nach Huffman]]. | |
| − | + | *Insbesondere wird auf die Seite [[Informationstheorie/Entropiecodierung_nach_Huffman#Anwendung_der_Huffman.E2.80.93Codierung_auf_k.E2.80.93Tupel|Anwendung der Huffman-Codierung auf k-Tupel]] Bezug genommen. | |
| − | + | *Eine vergleichbare Aufgabenstellung mit binären Eingangssymbolen wird in der [[Aufgaben:2.7_Huffman-Anwendung_für_binäre_Zweiertupel|Aufgabe 2.7]] behandelt. | |
| − | + | *Bezeichnen Sie die möglichen Zweiertupel mit <b>XX</b> = <b>A</b>, <b>XY</b> = <b>B</b>, <b>XZ</b> = <b>C</b>, <b>YX</b> = <b>D</b>, <b>YY</b> = <b>E</b>, <b>YZ</b> = <b>F</b>, <b>ZX</b> = <b>G</b>, <b>ZY</b> = <b>H</b>, <b>ZZ</b> = <b>I</b> . | |
| − | + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | |
| − | |||
| Zeile 68: | Zeile 69: | ||
<b>3.</b> Die Grafik zeigt den Huffman–Baum für die Anwendung mit <i>k</i> = 2. | <b>3.</b> Die Grafik zeigt den Huffman–Baum für die Anwendung mit <i>k</i> = 2. | ||
| − | [[Datei:P_ID2459__Inf_Z_2_7c.png| | + | [[Datei:P_ID2459__Inf_Z_2_7c.png|Huffman–Baum für Ternärquelle und Zweiertupel]] |
Damit erhält man | Damit erhält man | ||
Version vom 24. Mai 2017, 11:42 Uhr
Wir betrachten den gleichen Sachverhalt wie in der Aufgabe A2.7: Der Huffman–Algorithmus führt zu einem besseren Ergebnis, das heißt zu einer kleineren mittleren Codewortlänge $L_{\rm M}$, wenn man ihn nicht auf einzelne Symbole anwendet, sondern vorher $k$–Tupel bildet. Dadurch erhöht man den Symbolumfang von $M$ auf $M' = M^k$.
Für die hier betrachtete Nachrichtenquelle gilt:
- Symbolumfang: $M = 3$,
- Symbolvorrat: $\{$X, Y, Z$\}$,
- Wahrscheinlichkeiten: $p_{\rm X} = 0.7$, $p_{\rm Y} = 0.2$, $p_{\rm Z} = 0.1$,
- Entropie: $H = 1.157 \ \rm bit/Ternärsymbol$.
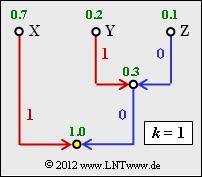
Die Grafik zeigt den Huffman–Baum, wenn man den Huffman–Algorithmus auf Einzelsymbole anwendet, also den Fall $k= 1$. In der Teilaufgabe (2) sollen Sie den entsprechenden Huffman–Code angeben, wenn vorher Zweiertupel gebildet werden ($k=2$).
Hinweise:
- Die Aufgabe gehört zum Kapitel Entropiecodierung nach Huffman.
- Insbesondere wird auf die Seite Anwendung der Huffman-Codierung auf k-Tupel Bezug genommen.
- Eine vergleichbare Aufgabenstellung mit binären Eingangssymbolen wird in der Aufgabe 2.7 behandelt.
- Bezeichnen Sie die möglichen Zweiertupel mit XX = A, XY = B, XZ = C, YX = D, YY = E, YZ = F, ZX = G, ZY = H, ZZ = I .
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$L_{\rm M} = p_{\rm X} \cdot 1 + (p_{\rm Y} + p_{\rm Z}) \cdot 2 \hspace{0.15cm}\underline{= 1.3\,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$
Dieser Wert liegt noch deutlich über der Quellenentropie H = 1.157 bit/Quellensymbol.
2. Es gibt M ′ = M 2 = 32 = 9 Zweiertupel mit folgenden Wahrscheinlichkeiten:
- pA = Pr(XX) = 0.49, pB = Pr(XY) = 0.14, pC = Pr(XZ) = 0.07,
- pD = Pr(YX) = 0.14, pE = Pr(YY) = 0.04, pF = Pr(YZ) = 0.02,
- pG = Pr(YX) = 0.07, pH = Pr(YY) = 0.02, pI = Pr(YZ) = 0.01.
3. Die Grafik zeigt den Huffman–Baum für die Anwendung mit k = 2.
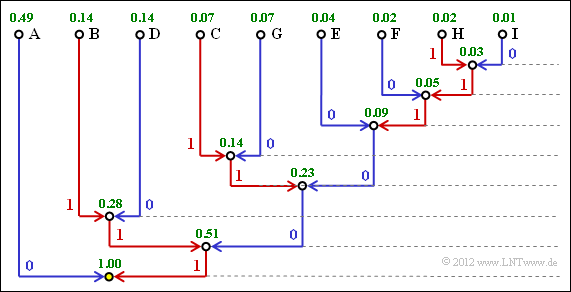 Damit erhält man
Damit erhält man
- für die einzelnen Zweiertupels folgende Binärcodierungen:
- für die einzelnen Zweiertupels folgende Binärcodierungen:
- XX = A → 0, XY = B → 111, XZ = C → 1011, YX = D → 110, YY = E → 1000,
- YZ = F → 10010, ZX = G → 1010, ZY = H → 100111, ZZ = I → 100110 .
- für die mittlere Codewortlänge:
- $$L_{\rm M}' \hspace{0.2cm} = \hspace{0.2cm} 0.49 \cdot 1 + (0.14 + 0.14) \cdot 3 + (0.07 + 0.04 + 0.07) \cdot 4 + \\ \hspace{0.2cm} + \hspace{0.2cm}0.02 \cdot 5 + (0.02 + 0.01) \cdot 6 = 2.33\,\,{\rm bit/Zweiertupel}$$
- $$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}'}/{2}\hspace{0.15cm}\underline{ = 1.165\,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$
4. Richtig ist Aussage 1, auch wenn LM mit wachsendem k nur sehr langsam abfällt.
- Die letzte Aussage ist falsch, da LM auch für k → ∞ nicht kleiner sein kann als H = 1.157 bit/Quellensymbol.
- Aber auch die zweite Aussage ist falsch: Da mit k = 2 weiterhin LM > H gilt, führt k = 3 zu einer Verbesserung.