Aufgaben:Aufgabe 2.13: Burrows-Wheeler-Rücktransformation: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2478__Inf_A_2_14.png|right|]] | + | [[Datei:P_ID2478__Inf_A_2_14.png|right|Zu analysierendes BWT-Ergebnis]] |
| − | Die Burrows–Wheeler–Transformation – abgekürzt BWT – bewirkt eine blockweise Sortierung der Zeichen eines Textes mit dem Ziel, den Text für die effiziente Datenkomprimierung mit Hilfe einer Lauflängencodierung oder einer Entropiecodierung aufzubereiten. | + | Die ''Burrows–Wheeler–Transformation'' – abgekürzt BWT – bewirkt eine blockweise Sortierung der Zeichen eines Textes mit dem Ziel, den Text für die effiziente Datenkomprimierung mit Hilfe einer Lauflängencodierung oder einer Entropiecodierung aufzubereiten. |
| − | + | * Zunächst wird aus einem Block der Länge $N$ eine $N×N$–Matrix erzeugt, wobei sich jede Zeile dieser ersten BWT–Matrix aus der Vorgängerzeile durch zyklische Linksverschiebung ergibt. | |
| − | + | * Danach wird die Matrix lexikografisch (ohne Sonderzeichen: alphabetisch) sortiert. Das Ergebnis der BWT ist die letzte Zeile der neuen BWT–Matrix, die so genannte <i>L–Spalte</i>. | |
| − | + | * Weiter wird in dieser Aufgabe auf die <i>F–Spalte</i> (von „First”, erste Zeile der BWT–Matrix) Bezug genommen, die man für die inverse Burrows–Wheeler–Transformation benötigt ⇒ Rekonstruktion des Originaltextes aus der L–Spalte (von „Last”, Letzte Zeile der BWT–Matrix) . | |
| − | + | * Für die inverse BWT benötigt man ferner den so genannten <i>Primärindex</i> $I$. Dieser gibt diejenige Zeile der BWT–Matrix an, in welcher der Algorithmus gestartet werden muss. | |
| − | Die Grafik zeigt das Ergebnis einer BWT, genauer gesagt | + | |
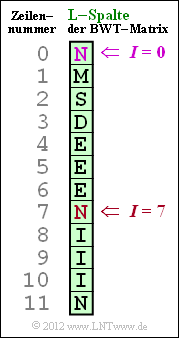
| + | Die Grafik zeigt das Ergebnis einer BWT, genauer gesagt deren L–Spalte. Aus dieser soll der Originaltext entsprechend der Beschreibung auf der Theorieseite [[Informationstheorie/Weitere_Quellencodierverfahren#Burrows.E2.80.93Wheeler.E2.80.93Transformation|Burrows–Wheeler–Transformation]] rekonstruiert werden, wobei in Teilaufgabe (2) von Primärindex $I = 7$ und in Teilaufgabe (3) von $I = 0$ auszugehen ist. | ||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Informationstheorie/Weitere_Quellencodierverfahren|Weitere Quellencodierverfahren]]. | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Weitere_Quellencodierverfahren|Weitere Quellencodierverfahren]]. | ||
| − | *Insbesondere wird Bezug genommen auf die Seite [[Informationstheorie/Weitere_Quellencodierverfahren# | + | *Insbesondere wird Bezug genommen auf die Seite [[Informationstheorie/Weitere_Quellencodierverfahren#Burrows.E2.80.93Wheeler.E2.80.93Transformation|Burrows–Wheeler–Transformation]]. |
| − | * | + | *Weitere Informationen finden Sie in den beiden nachfolgend genannten Veröffentlichungen: |
| − | + | : Abel, J.: ''Verlustlose Datenkompression auf Grundlage der Burrows-Wheeler-Transformation''. <br> In: PIK - Praxis der Informationsverarbeitung und Kommunikation, no. 3, vol. 26, S. 140-144, Sept. 2003. | |
| − | < | + | : Abel, J.: ''Grundlagen des Burrows-Wheeler-Kompressionsalgorithmus''. <br> In: Informatik Forschung & Entwicklung, no. 2, vol. 18, S. 80-87, Jan. 2004. |
| Zeile 35: | Zeile 36: | ||
| − | {Wie lautet das Ergebnis der Rekonstruktion mit dem Primärindex | + | {Wie lautet das Ergebnis der Rekonstruktion mit dem Primärindex $I = 7$? |
|type="[]"} | |type="[]"} | ||
+ <b>MEINDEINSEIN</b>, | + <b>MEINDEINSEIN</b>, | ||
| Zeile 42: | Zeile 43: | ||
| − | {Was passiert, wenn bei der Rekonstruktion (BWT–Rücktransformation) vom falschen Primärindex | + | {Was passiert, wenn bei der Rekonstruktion (BWT–Rücktransformation) vom falschen Primärindex $I = 0$ ausgegangen wird? |
|type="[]"} | |type="[]"} | ||
- Es ergibt sich der Originaltext, von hinten nach vorne gelesen. | - Es ergibt sich der Originaltext, von hinten nach vorne gelesen. | ||
| Zeile 48: | Zeile 49: | ||
| − | {Warum ist die Burrows–Wheeler–Transformierte | + | {Warum ist die Burrows–Wheeler–Transformierte hinsichtlich einer späteren Datenkomprimierung besser geeignet als das Original? |
|type="[]"} | |type="[]"} | ||
- Es ergeben sich günstigere Zeichenhäufigkeiten. | - Es ergeben sich günstigere Zeichenhäufigkeiten. | ||
Version vom 28. Mai 2017, 12:55 Uhr
Die Burrows–Wheeler–Transformation – abgekürzt BWT – bewirkt eine blockweise Sortierung der Zeichen eines Textes mit dem Ziel, den Text für die effiziente Datenkomprimierung mit Hilfe einer Lauflängencodierung oder einer Entropiecodierung aufzubereiten.
- Zunächst wird aus einem Block der Länge $N$ eine $N×N$–Matrix erzeugt, wobei sich jede Zeile dieser ersten BWT–Matrix aus der Vorgängerzeile durch zyklische Linksverschiebung ergibt.
- Danach wird die Matrix lexikografisch (ohne Sonderzeichen: alphabetisch) sortiert. Das Ergebnis der BWT ist die letzte Zeile der neuen BWT–Matrix, die so genannte L–Spalte.
- Weiter wird in dieser Aufgabe auf die F–Spalte (von „First”, erste Zeile der BWT–Matrix) Bezug genommen, die man für die inverse Burrows–Wheeler–Transformation benötigt ⇒ Rekonstruktion des Originaltextes aus der L–Spalte (von „Last”, Letzte Zeile der BWT–Matrix) .
- Für die inverse BWT benötigt man ferner den so genannten Primärindex $I$. Dieser gibt diejenige Zeile der BWT–Matrix an, in welcher der Algorithmus gestartet werden muss.
Die Grafik zeigt das Ergebnis einer BWT, genauer gesagt deren L–Spalte. Aus dieser soll der Originaltext entsprechend der Beschreibung auf der Theorieseite Burrows–Wheeler–Transformation rekonstruiert werden, wobei in Teilaufgabe (2) von Primärindex $I = 7$ und in Teilaufgabe (3) von $I = 0$ auszugehen ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Quellencodierverfahren.
- Insbesondere wird Bezug genommen auf die Seite Burrows–Wheeler–Transformation.
- Weitere Informationen finden Sie in den beiden nachfolgend genannten Veröffentlichungen:
- Abel, J.: Verlustlose Datenkompression auf Grundlage der Burrows-Wheeler-Transformation.
In: PIK - Praxis der Informationsverarbeitung und Kommunikation, no. 3, vol. 26, S. 140-144, Sept. 2003. - Abel, J.: Grundlagen des Burrows-Wheeler-Kompressionsalgorithmus.
In: Informatik Forschung & Entwicklung, no. 2, vol. 18, S. 80-87, Jan. 2004.
Fragebogen
Musterlösung
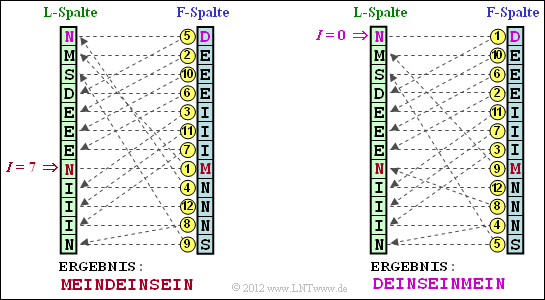
2. Richtig ist der Lösungsvorschlag 1: MEINDEINSEIN, wie aus der linken Darstellung hervorgeht. Beachten Sie, dass die obersten Zeile jeweils für die Zeilennummer „0” steht:
Zur Erklärung:
- Man beginnt die Decodierung mit der Zeile I = 7 der F–Spalte. Der Inhalt ist „M”.
- Man sucht das entsprechende „M” in der L–Spalte und findet es in der Zeilennummer „1”.
- Von Zeile 1 der L–Spalte geht man horizontal zur F–Spalte und findet das Symbol „E”.
- In gleicher Weise findet man das dritte Ausgabesymbol „I” in der Zeile 4 der F–Spalte.
- Der Decodieralgorithmus endet mit dem Ausgabesymbol „N” in der drittletzten Zeile.
3. Richtig ist der Lösungsvorschlag 2: DEINSEINMEIN, wie aus der rechten Grafik hervorgeht.
4. Richtig ist der Lösungsvorschlag 3. Bei der BWT sind hier vier Zeichen gleich ihren Vorgängern, im Original kein einziges. In der F–Spalte wären zwar aufgrund der lexikografischen Sortierung noch mehr Zeichen gleich wie die jeweiligen Vorgänger (insgesamt 6), aber diese Sortierung lässt sich nicht verlustlos rückgängig machen. Auch der Lösungsvorschlag 1 ist falsch: Original und BWT beinhalten genau die gleichen Zeichen (dreimal E,dreimal I, dreimal N sowie je einmal D, M und S).