Aufgaben:Aufgabe 3.8Z: Tupel aus ternären Zufallsgrößen: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 3.07Z Tupel aus ternären Zufallsgrößen nach 3.8Z Tupel aus ternären Zufallsgrößen) |
Version vom 31. Mai 2017, 15:25 Uhr
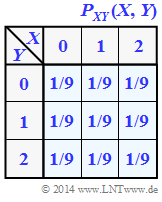
Wir betrachten das Tupel $Z = (X, Y)$, wobei die Einzelkomponenten $X$ und $Y$ jeweils ternäre Zufallsgrößen darstellen $\Rightarrow$ Symbolumfang $|X| = |Y| = 3$. Die gemeinsame Wahrscheinlichkeitsfunktion $P_{ XY }(X, Y)$ ist rechts angegeben.
In dieser Aufgabe sind zu berechnen:
- die Verbundentropie $H(XY)$ und die Transinformation $I(X; Y)$,
- die Verbundentropie $H(XZ)$ und die Transinformation $I(X; Z)$,
- die bedingten Entropien $H(Z|X)$ und $H(X|Z)$.
Hinweis: Die Aufgabe bezieht sich auf das Themengebiet von Kapitel 3.2.
Fragebogen
Musterlösung
$H(X) = log_2(3) = 1.585 (bit)$,
$H(Y) = log_2(3) = 1.585 (bit)$,
Die 2D–Zufallsgröße $XY = \{00, 01, 02, 10, 11, 12, 20, 21, 22\} \Rightarrow |XY| = |Z| = 9$ weist ebenfalls gleiche Wahrscheinlichkeiten auf: $p_{ 00 } = p_ { 01 } = ... = p_{ 22 } = 1/9$. Daraus folgt:
$H(XY) = log_2(9) = 3.170 (bit)$
2. Die Zufallsgrößen$X$und $Y$ sind wegen $P_{ XY }(⋅) = P_X(⋅) · P_Y(⋅)$ statistisch unabhängig $\Rightarrow I(X, Y) = 0$. Zum gleichen Ergebnis kommt man über die Gleichung $I(X; Y) = H(X) + H(Y) – H(XY)$.
3. Interpretiert man $I(X; Z)$ als die verbleibende Unsicherheit hinsichtlich des Tupels $Z$, wenn die erste Komponente $X$ bekannt ist, so gilt offensichtlich$ I(X; Z) = H(Y) = 1.585 bit$.
Rein formal lässt sich diese Aufgabe auch wie folgt lösen:
- Die Entropie $H(Z)$ ist gleich $H(XY) = 3.170 bit$.
- Die Verbundwahrscheinlichkeit $P_{ XZ }(X, Z)$ beinhaltet neun Elemente der Wahrscheinlichkeit $1/9$, alle anderen sind mit Nullen belegt (Rechte Grafik) $\Rightarrow H(XZ) = log2 (9) = 3.170 bit$.
- Damit gilt für die Transinformation (gemeinsame Information der Zufalsgrößen $X$ und $Z$):
$$I(X;Z) = H(X) + H(Z) - H(XZ) = $$ $$= 1.585 +3.170 - 3170 = 1.585 (bit)$$
4.Entsprechend der rechten Grafik gilt:
$$H(Z|X) = H(XZ)- H(X) = 3.170 - 1.585 = 1.585 (bit)$$ $$H(X|Z) = H(XZ) - H(Z) = 3.170 - 3.170 = 0 (bit)$$
- $H(Z|X)$ gibt die Restunsicherheit hinsichtlich des Tupels $Z$ an, wenn man die erste Komponente $X$kennt. Die Unsicherheit hinsichtlich des Tupels $Z$ ist $H(Z) = 2 · log_2 (3) bit$, bei Kenntnis der Komponente $X$ halbiert sich die Unsicherheit auf $H(Z|X) = log2 (3) bit$.
- $H(X|Z)$gibt die verbleibende Unsicherheit hinsichtlich der Komponente $X$ an, wenn man das Tupel $Z = (X, Y)$ kennt. Diese Unsicherheit ist natürlich $0$: Kennt man $Z$, so kennt man auch $X$.