Aufgaben:Aufgabe 3.11Z: Extrem unsymmetrischer Kanal

• Zurück zum Buch

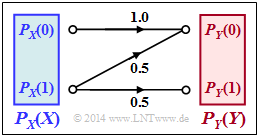
Betrachtet wird der nebenstehend gezeichnete Kanal mit den folgenden Eigenschaften:

• Das Symbol $X = 0$ wird immer richtig übertragen und führt stets zum Ergebnis $Y = 0$.
• Das Symbol $X = 1$ wird maximal verfälscht. Aus Sicht der Informationstheorie bedeutet diese Aussage:

$${\rm Pr}(Y \hspace{-0.05cm} = 0\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) ={\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) = 0.5 \hspace{0.05cm}$$

Zu bestimmen sind in dieser Aufgabe:

• die Transinformation $I(X; Y)$für $P_X(0) = p_0 = 0.4$ und $P_X(1) = p_1 = 0.6$. Es gilt allgemein:

$$ I(X;Y) \hspace{-0.15cm} =\hspace{-0.15cm} H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}$$

$$I(X;Y) \hspace{-0.15cm} = \hspace{-0.15cm} H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$$ $$I(X;Y) \hspace{-0.15cm} =\hspace{-0.15cm} H(X) + H(Y)- H(XY)\hspace{0.05cm}$$

• die Kanalkapazität:

$$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Anwendung auf die Digitalsignalübertragung.
• Bezug genommen wird insbesondere auf die Seite Informationstheoretisches Modell der Digitalsignalübertragung.
• Im obigen Schaubild sind Auslöschungen (Wahrscheinlichkeit $λ$) blau gezeichnet und „richtige Übertragungswege” (also von $X = μ$ nach $Y = μ$) blau ($1 ≤ μ ≤ M$).
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Hinweis: Die Aufgabe beschreibt einen Teilaspekt von Kapitel 3.3. In der Aufgabe A3.13 sollen die hier gefundenen Ergebnisse im Vergleich zum BSC–Kanal interpretiert werden

Fragebogen

1

Berechnen Sie die Quellenentropie allgemein und für $p_0 = 0.4$.

$H(X) \ = \ $ $\ \rm bit$

2

Berechnen Sie die Sinkenentropie allgemein und für $p_0 = 0.4$.

$H(Y) \ = \ $ $\ \rm bit$

3

Berechnen Sie die Verbundentropie allgemein und für$p_0 = 0.4$.

$H(XY) \ = \ $ $\ \rm bit$

4

Berechnen Sie die Transinformation allgemein und für $p_0 = 0.4$.

$I(X; Y) \ = \ $ $\ \rm bit$

5

Welche Wahrscheinlichkeit $p_0^{(*)}$ führt zur Kanalkapazität $C$?

$p_0^{(*)} \ = \ $

6

Wie groß ist die Kanalkapazität des vorliegenden Kanals?

$C \ = \ $ $\ \rm bit$

7

Wie groß sind die bedingten Entropien mit $p_0 = p_0^{(*)}$ gemäß Teilaufgabe (5)?

$H(X|Y) \ = \ $ $\ \rm bit$

$H(Y|X) \ = \ $ $\ \rm bit$

Musterlösung

Musterlösung

1. Die Quellenentropie ergibt sich entsprechend der binären Entropiefunktion: $$H(X) = H_{\rm bin}(p_0)= H_{\rm bin}(0.4) \hspace{0.15cm} \underline {=0.971\,{\rm bit}} \hspace{0.05cm}$$ 2.Die Wahrscheinlichkeiten der Sinkensymbole sind: $$P_Y(1) = p_1/2 = (1 - p_0)/2 = 0.3\hspace{0.05cm},\hspace{0.2cm} P_Y(0) = 1-P_Y(1) = p_1/2 = (1 - p_0)/2 = 0.7$$ $$\Rightarrow \hspace{0.3cm} H(Y) = H_{\rm bin}(\frac{1+p_0}{2})= H_{\rm bin}(0.7) \hspace{0.15cm} \underline {=0.881\,{\rm bit}} \hspace{0.05cm}$$ 3. Die Verbundwahrscheinlichkeiten $p_{μκ} = Pr[(X = μ) ∩ (Y = κ)]$ ergeben sich zu: $$ p_{00} = p_0 \hspace{0.05cm},\hspace{0.3cm} p_{01} = 0 \hspace{0.05cm},\hspace{0.3cm} p_{10} = (1 - p_0)/2 \hspace{0.05cm},\hspace{0.3cm} p_{11} = (1 - p_0)/2$$ $$\Rightarrow \hspace{0.3cm} H(XY) \hspace{-0.15cm}=\hspace{-0.15cm} p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ p_0} + 2 \cdot \frac{1-p_0}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{ 1- p_0} =$$ $$=\hspace{-0.15cm} p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ p_0} + (1-p_0) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ 1- p_0} + (1-p_0) \cdot {\rm log}_2 \hspace{0.1cm} (2) =$$ $$=\hspace{-0.15cm}H_{\rm bin}(p_0) + 1 - p_0 \hspace{0.05cm}$$ Das numerische Ergebnis für $p_0 = 0.4$ ist somit: $$H(XY) = H_{\rm bin}(0.4) + 0.6 = 0.971 + 0.6 \hspace{0.15cm} \underline {=1.571\,{\rm bit}} \hspace{0.05cm}$$

4.Eine (mögliche) Gleichung zur Berechnung der Transinformation lautet: $$ I(X;Y) = H(X) + H(Y)- H(XY)\hspace{0.05cm}$$ Daraus erhält man mit den Ergebnissen der Teilaufgaben (a), (b) und (c): $$I(X;Y) = H_{\rm bin}(p_0) + H_{\rm bin}(\frac{1+p_0}{2}) - H_{\rm bin}(p_0) -1 + p_0 = H_{\rm bin}(\frac{1+p_0}{2}) -1 + p_0$$ $$ \Rightarrow \hspace{0.3cm} p_0 = 0.4 {\rm :}\hspace{0.5cm} I(X;Y) = H_{\rm bin}(0.7) - 0.6 = 0.881 - 0.6 \hspace{0.15cm} \underline {=0.281\,{\rm bit}}\hspace{0.05cm}$$ 5 Die Kanalkapazität $C$ ist die Transinformation $I(X; Y) $bei bestmöglichen Wahrscheinlichkeiten $p_0$ und $p_1$ der Quellensymbole. Nach Differentiation erhält man die Bestimmungsgleichung: $$\frac{d}{d_{p_0}} I(X;Y) = \frac{d}{d_{p_0}} H_{bin}(\frac{1+p_0}{2} +1\stackrel{!}{=} 0.$$ Mit dem Differentialquotienten der binären Entropiefunktion $$ \frac{d}{d_p}H_{bin} = log_2 \frac{1-p}{p}, $$ und entsprechendes Nachdifferenzieren erhält man : $$\frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{(1-p_0)/2}{1- (1-p_0)/2} +1 \stackrel{!}{=} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{(1-p_0)/2}{(1+p_0)/2} +1 \stackrel{!}{=} 0$$ $$ \Rightarrow \hspace{0.3cm} {\rm log}_2 \hspace{0.1cm} \frac{1+p_0}{1-p_0} \stackrel{!}{=} 2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{1+p_0}{1-p_0} \stackrel{!}{=} 4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_0 \hspace{0.15cm} \underline {=0.6}\hspace{0.05cm}$$ 6. Für die Kanalkapazität gilt dementsprechend: $$C = I(X;Y) \big |_{p_0 \hspace{0.05cm}=\hspace{0.05cm} 0.6} = H_{\rm bin}(0.8) - 0.4 = 0.722 -0.4 \hspace{0.15cm} \underline {=0.322\,{\rm bit}}\hspace{0.05cm}$$ In Aufgabe A3.13 wird dieses Ergebnis im Vergleich zum BSC–Kanalmodell interpretiert. 7. Für die Äquivokation gilt: $$ H(X \hspace{-0.1cm}\mid \hspace{-0.1cm}Y) = H(X) - I(X;Y) = 0.971 -0.322 \hspace{0.15cm} \underline {=0.649\,{\rm bit}}\hspace{0.05cm}$$ Wegen $H_{bin}(0.4) = H_{bin}(0.6)$ ergibt sich die gleiche Quellenentropie $H(X)$ wie in Teilaufgabe (a). Die Sinkenentropie muss neu berechnet werden. Mit $p_0 = 0.6$ erhält man $H(Y) = H_{bin}(0.8) = 0.722 bit$, und damit ergibt sich für die Irrelevanz: $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(Y) - I(X;Y) = 0.722 -0.322 \hspace{0.15cm} \underline {=0.400\,{\rm bit}}\hspace{0.05cm}$$