Aufgaben:Aufgabe 2.9: Symmetrische Verzerrungen: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 2.8Z Symmetrische Verzerrungen nach 2.9 Symmetrische Verzerrungen) |
|||
| Zeile 2: | Zeile 2: | ||
}} | }} | ||
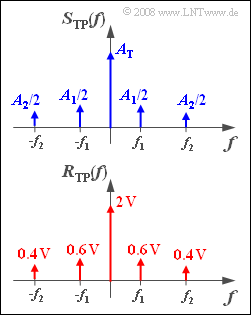
| − | [[Datei:P_ID1040__Mod_Z_2_8.png|right|]] | + | [[Datei:P_ID1040__Mod_Z_2_8.png|right|frame|Sende– und Empfangsspektrum im äquivalenten TP-Bereich]] |
Das aus zwei Anteilen zusammengesetzte Quellensignal | Das aus zwei Anteilen zusammengesetzte Quellensignal | ||
| − | $$q(t) = A_1 \cdot \cos(2 \pi f_1 t ) + A_2 \cdot \cos(2 \pi f_2 t )$$ | + | :$$q(t) = A_1 \cdot \cos(2 \pi f_1 t ) + A_2 \cdot \cos(2 \pi f_2 t )$$ |
| − | wird amplitudenmoduliert und über einen linear verzerrenden Übertragungskanal übertragen. Die Trägerfrequenz ist $ | + | wird amplitudenmoduliert und über einen linear verzerrenden Übertragungskanal übertragen. Die Trägerfrequenz ist $f_{\rm T}$ und der zugesetzte Gleichanteil $A_{\rm T}$. Es liegt also eine ''Zweiseitenband-Amplitudenmoduluation'' (ZSB–AM) ''mit Träger'' vor. |
| − | Die obere Grafik zeigt das Spektrum $S_{TP}(f)$ des äquivalenten TP–Signals in schematischer Form. Das bedeutet, dass die Längen der gezeichneten Diraclinien nicht den tatsächlichen Werten von $ | + | Die obere Grafik zeigt das Spektrum $S_{\rm TP}(f)$ des äquivalenten TP–Signals in schematischer Form. Das bedeutet, dass die Längen der gezeichneten Diraclinien nicht den tatsächlichen Werten von $A_{\rm T}$, $A_1/2$ und $A_2/2$ entsprechen. |
| − | Messtechnisch erfasst wurde die Spektralfunktion $R(f)$ des Empfangssignals. In der unteren Grafik sehen Sie das daraus berechnete äquivalente Tiefpass–Spektrum $R_{TP}(f)$. | + | Messtechnisch erfasst wurde die Spektralfunktion $R(f)$ des Empfangssignals. In der unteren Grafik sehen Sie das daraus berechnete äquivalente Tiefpass–Spektrum $R_{\rm TP}(f)$. |
Der Kanalfrequenzgang ist durch einige Stützwerte ausreichend genau beschrieben: | Der Kanalfrequenzgang ist durch einige Stützwerte ausreichend genau beschrieben: | ||
| − | $$ H_{\rm K}(f = f_{\rm T}) = 0.5,\hspace{0.3cm}H_{\rm K}(f = f_{\rm T} \pm f_1) = 0.4,\hspace{0.3cm} H_{\rm K}(f = f_{\rm T} \pm f_2) = 0.2 \hspace{0.05cm}.$$ | + | :$$ H_{\rm K}(f = f_{\rm T}) = 0.5,\hspace{0.3cm}H_{\rm K}(f = f_{\rm T} \pm f_1) = 0.4,\hspace{0.3cm} H_{\rm K}(f = f_{\rm T} \pm f_2) = 0.2 \hspace{0.05cm}.$$ |
| Zeile 21: | Zeile 21: | ||
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| Zeile 29: | Zeile 28: | ||
{ Ermitteln Sie die Amplituden von Träger– und Quellensignal. | { Ermitteln Sie die Amplituden von Träger– und Quellensignal. | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_{\rm T} \ = \ $ { 4 3% } $\ \rm V$ |
| − | $A_1$ | + | $A_1 \ = \ $ { 3 3% } $\ \rm V$ |
| − | $A_2$ | + | $A_2 \ = \ $ { 4 3% } $\ \rm V$ |
| − | {Zu welcher Art von Verzerrung hätte der Einsatz eines Hüllkurvendemodulators bei idealem Kanal $ | + | {Zu welcher Art von Verzerrung hätte der Einsatz eines Hüllkurvendemodulators bei idealem Kanal ⇒ $H_{\rm K}(f) = 1$ geführt? |
|type="[]"} | |type="[]"} | ||
- Keine Verzerrungen. | - Keine Verzerrungen. | ||
| Zeile 41: | Zeile 40: | ||
{Berechnen Sie das äquivalente Tiefpass–Signal und beantworten Sie folgende Fragen. Ist es zutreffend, dass | {Berechnen Sie das äquivalente Tiefpass–Signal und beantworten Sie folgende Fragen. Ist es zutreffend, dass | ||
|type="[]"} | |type="[]"} | ||
| − | + $r_{TP}(t)$ stets reell ist, | + | + $r_{\rm TP}(t)$ stets reell ist, |
| − | + $r_{TP}(t)$ stets größer oder gleich 0 ist, | + | + $r_{\rm TP}(t)$ stets größer oder gleich 0 ist, |
| − | - die Phasenfunktion $ϕ(t)$ die Werte | + | - die Phasenfunktion $ϕ(t)$ die Werte $0^\circ$ und $180^\circ$ annehmen kann. |
{Zu welchen Verzerrungen führt der Hüllkurvendemodulator beim betrachteten Übertragungskanal? | {Zu welchen Verzerrungen führt der Hüllkurvendemodulator beim betrachteten Übertragungskanal? | ||
Version vom 2. Juli 2017, 12:54 Uhr
Das aus zwei Anteilen zusammengesetzte Quellensignal
- $$q(t) = A_1 \cdot \cos(2 \pi f_1 t ) + A_2 \cdot \cos(2 \pi f_2 t )$$
wird amplitudenmoduliert und über einen linear verzerrenden Übertragungskanal übertragen. Die Trägerfrequenz ist $f_{\rm T}$ und der zugesetzte Gleichanteil $A_{\rm T}$. Es liegt also eine Zweiseitenband-Amplitudenmoduluation (ZSB–AM) mit Träger vor.
Die obere Grafik zeigt das Spektrum $S_{\rm TP}(f)$ des äquivalenten TP–Signals in schematischer Form. Das bedeutet, dass die Längen der gezeichneten Diraclinien nicht den tatsächlichen Werten von $A_{\rm T}$, $A_1/2$ und $A_2/2$ entsprechen.
Messtechnisch erfasst wurde die Spektralfunktion $R(f)$ des Empfangssignals. In der unteren Grafik sehen Sie das daraus berechnete äquivalente Tiefpass–Spektrum $R_{\rm TP}(f)$.
Der Kanalfrequenzgang ist durch einige Stützwerte ausreichend genau beschrieben:
- $$ H_{\rm K}(f = f_{\rm T}) = 0.5,\hspace{0.3cm}H_{\rm K}(f = f_{\rm T} \pm f_1) = 0.4,\hspace{0.3cm} H_{\rm K}(f = f_{\rm T} \pm f_2) = 0.2 \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Hüllkurvendemodulation.
- Bezug genommen wird insbesondere auf das Kapitel Beschreibung mit Hilfe des äquivalenten Tiefpass-Signals.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
2.Der Modulationsgrad ergibt sich zu $m = (A_1 + A_2)/A_T = 1.75$. Damit ergeben sich bei Verwendung eines Hüllkurvendemodulators starke nichtlineare Verzerrungen. Ein Klirrfaktor kann nicht angegeben werden, da das Quellensignal zwei Frequenzanteile beinhaltet.
3. Die Fourierrücktransformation von $R_{TP}(f)$ führt zum Ergebnis:
$$ r_{\rm TP}(t) = 2 \,{\rm V} + 1.2 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 0.8 \,{\rm V} \cdot \cos(2 \pi f_2 t )\hspace{0.05cm}.$$
Diese Funktion ist stets reell und nicht–negativ. Damit gilt gleichzeitig $ϕ(t) = 0$. Dagegen ist $ϕ(t) = 180°$ nicht möglich. Richtig sind also die Aussagen 1 und 2.
4.Ein Vergleich der beiden Signale $$q(t) = 3 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 4 \,{\rm V} \cdot \cos(2 \pi f_2 t ),$$ $$ v(t) = 0.4 \cdot 3 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 0.2 \cdot 4 \,{\rm V} \cdot \cos(2 \pi f_2 t )$$ zeigt, dass nun lineare Verzerrungen – genauer gesagt Dämpfungsverzerrungen – auftreten.
Der Kanal $H_K(f)$ hat hier den positiven Effekt, dass anstelle von irreversiblen nichtlinearen Verzerrungen nun nichtlineare Verzerrungen entstehen, die durch ein nachgeschaltetes Filter eliminiert werden können. Dies ist darauf zurückzuführen, dass durch die stärkere Dämpfung des Quellensignals $q(t)$ im Vergleich zum Trägersignal $z(t)$ der Modulationsgrad von $m = 1.75$ auf $m = (0.4 · 3 V + 0.2 · 4 V)/(0.5 · 4 V) = 1$ vermindert wird.