Aufgaben:Aufgabe 2.10: ESB-AM mit Kanalverzerrungen

• Zurück zum Buch

Sendespektrum des analytischen Signals und Kanalfrequenzgang

Wir betrachten die Übertragung des Quellensignals

$$q(t) = 2\,{\rm V} \cdot \cos(2 \pi f_2 t) + 2\,{\rm V} \cdot \cos(2 \pi f_4 t)$$

über einen Gauß–Bandpasskanal mit der Mittenfrequenz $f_{\rm M} = 48 \ \rm kHz$. Diese unterscheidet sich von der bei der Modulation verwendeten Trägerfrequenz $f_{\rm T} = 50 \ \rm kHz$. Die Frequenzen $f_2$ und $f_4$ stehen als Abkürzungen für $f = 2 \ \rm kHz$ bzw. $f = 4 \ \rm kHz$.

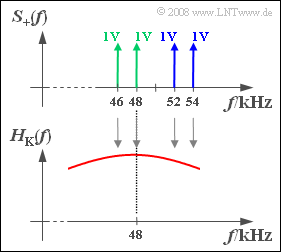
Untersucht werden sollen folgende Modulationsverfahren mit dem jeweiligen Spektrum $S_+(f)$ – des analytischen Signals – entsprechend der oberen Grafik:

• ZSB–AM (alle vier Spektrallinien bei $46 \ \rm kHz$, $48 \ \rm kHz$, $52 \ \rm kHz$ und $54 \ \rm kHz$),
• OSB–AM (nur blaue Spektrallinien bei $52 \ \rm kHz$ und $54 \ \rm kHz$),
• USB–AM (nur grüne Spektrallinien bei $46 \ \rm kHz$ und $48 \ \rm kHz$).

Verwendet wird jeweils ein Synchrondemodulator, der zunächst das empfängerseitige Trägersignal

$$ z_{\rm E} (t) = \left\{ \begin{array}{c} 2 \cdot z(t) \\ 4 \cdot z(t) \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm ZSB} \hspace{0.05cm}, \\ {\rm OSB, USB} \hspace{0.05cm} \\ \end{array}$$

multiplikativ zusetzt und anschließend die Anteile um die doppelte Trägerfrequenz vollständig unterdrückt. Bei idealem Kanal $H_{\rm K}(f) = 1$ würde somit in allen Fällen $v(t) = q(t)$ gelten.

Der hier betrachtete Gaußkanal ist durch folgende Stützwerte gegeben:

$$ H_{\rm K}(f = 46\,{\rm kHz}) = 0.968,\hspace{0.3cm}H_{\rm K}(f = 48\,{\rm kHz}) = 1.000,$$

$$ H_{\rm K}(f = 52\,{\rm kHz}) = 0.882,\hspace{0.3cm}H_{\rm K}(f = 54\,{\rm kHz}) = 0.754\hspace{0.05cm}.$$

Schreiben Sie das Sinkensignal jeweils in der Form

$$v(t) = A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2)) + A_4 \cdot \cos(2 \pi f_4 \cdot (t - \tau_4))\hspace{0.05cm}.$$

Alle Berechnungen sind sowohl für eine perfekte Phasensynchronisation ($Δϕ_{\rm T} = 0$) als auch für einen Phasenversatz von $Δϕ_{\rm T} = 30^\circ$ durchzuführen. Dieser liegt zum Beispiel dann vor, wenn das sendeseitige Trägersignal cosinusförmig verläuft und für das empfangsseitige Trägersignal gilt:

$$ z_{\rm E} (t) = A_{\rm E} \cdot \cos(\omega_{\rm T} \cdot t - 30^\circ) . $$

Hinweise:

• Die Aufgabe gehört zum Kapitel Einseitenbandmodulation.
• Bezug genommen wird aber auch auf das Kapitel Synchrondemodulation.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Berechnen Sie die Amplituden bei ZSB–AM und perfekter Synchronisation ($Δϕ_{\rm T} = 0$).

$A_2 \ = \ $ $\ \rm V$

$A_4 \ = \ $ $\ \rm V$

2

Wie lauten die Größen $A_2$ und $τ_2$ bei ZSB–AM und Phasenversatz ($Δϕ_{\rm T} = 30^\circ$)?

$A_2 \ = \ $ $\ \rm V$

$τ_2 \hspace{0.25cm} = \ $ $\ \rm μs$

3

Berechnen Sie die Amplituden $A_2$ und $A_4$ bei OSB–AM und perfekter Synchronisation ($Δϕ_{\rm T} = 0$).

$A_2 \ = \ $ $\ \rm V$

$A_4 \ = \ $ $\ \rm V$

4

Geben Sie die Signalsamplituden für USB–AM und perfekter Synchronisation ($Δϕ_{\rm T} = 0$) an.

$A_2 \ = \ $ $\ \rm V$

$A_4 \ = \ $ $\ \rm V$

5

Wie lauten dagegen die Signalparameter bei USB–AM und Phasenversatz ($Δϕ_{\rm T} = 30^\circ$)?

$A_2 \ = \ $ $\ \rm V$

$τ_2 \hspace{0.25cm} = \ $ $\ \rm μs$

$A_4 \ = \ $ $\ \rm V$

$τ_4 \hspace{0.25cm} = \ $ $\ \rm μs$

6

Welche dieser Aussagen sind nach Ihren Ergebnissen zutreffend? Hierbei sollen unter „Kanalverzerrungen” stets Dämpfungsverzerrungen verstanden werden.

	Kanalverzerrung führt bei ZSB-AM zu Dämpfungsverzerrungen.
	Kanalverzerrung führt bei ESB–AM zu Phasenverzerrungen.
	Ein Phasenversatz führt bei ZSB–AM zu Dämpfungsverzerrungen.
	Ein Phasenversatz führt bei ESB–AM zu Phasenverzerrungen.

Musterlösung

Musterlösung

(1)  Bei der ZSB–AM sind folgende Dämpfungsfaktoren zu berücksichtigen:

$$\alpha_2 = {1}/{2} \cdot \left[ H_{\rm K}(f = 48\,{\rm kHz}) + H_{\rm K}(f = 52\,{\rm kHz})\right] = 0.981,$$

$$\alpha_4 = {1}{2} \cdot \left[ H_{\rm K}(f = 46\,{\rm kHz}) + H_{\rm K}(f = 54\,{\rm kHz})\right] = 0.861\hspace{0.05cm}.$$

Damit ergeben sich die Amplituden $A_2\hspace{0.15cm}\underline{ = 1.882 \ \rm V}$ und $A_4\hspace{0.15cm}\underline{ = 1.722 \ \rm V}$

(2)  Bei ZSB führt ein Phasenversatz zwischen den Trägerfrequenzen von Sender und Empfänger nur zu einer für alle Frequenzen gleichen Dämpfung:

$$A_2 = \cos (30^\circ) \cdot 1.882\,{\rm V} \hspace{0.15cm}\underline {= 1.630\,{\rm V}},$$

$$A_4 = \cos (30^\circ) \cdot 1.722\,{\rm V} = 1.491\,{\rm V}\hspace{0.05cm}.$$

Die Laufzeiten sind $τ_2\hspace{0.15cm}\underline {= 0}$ und $τ_4 = 0$.

(3)  Bei OSB–AM wird der Dämpfungsfaktor $α_2$ allein von $H_{\rm K}(f = 52\ \rm kHz)$ bestimmt. Da der prinzipielle Amplitudenverlust der OSB um den Faktor $2$ durch eine größere Trägeramplitude ausgeglichen wird, gilt:

$$A_2 = 0.882 \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.764\,{\rm V}},$$

$$A_4 = 0.754 \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.508\,{\rm V}} \hspace{0.05cm}.$$

(4)  Analog zur Lösung der Teilaufgabe (3) erhält man hier:

$$ A_2 = H_{\rm K}(f = 48\,{\rm kHz}) \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 2\,{\rm V}},$$

$$A_4 = H_{\rm K}(f = 46\,{\rm kHz}) \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.936\,{\rm V}} \hspace{0.05cm}.$$

(5)  Bei der USB–AM lautet das Empfangssignal:

$$r(t) = 1\,{\rm V} \cdot \cos( \omega_{\rm 48} \cdot t) + 0.968\,{\rm V} \cdot \cos( \omega_{\rm 46} \cdot t)\hspace{0.05cm}.$$

Durch Multiplikation mit dem empfangsseitigen Trägersignal $z_{\rm E}(t) = 4 \cdot \cos( \omega_{\rm 50} \cdot t - \Delta \phi_{\rm T})$ erhält man nach Anwendung des trigonometrischen Additionstheorems:

$$v(t) = r(t) \cdot z_{\rm E}(t) = \hspace{0.15cm}\underline { 2.000\,{\rm V}} \cdot \cos( \omega_{\rm 2} \cdot t - \Delta \phi_{\rm T})+\hspace{0.15cm}\underline { 1.936\,{\rm V}} \cdot \cos( \omega_{\rm 4} \cdot t - \Delta \phi_{\rm T}) + {\rm Anteile \hspace{0.15cm}um \hspace{0.15cm}} 2f_{\rm T}\hspace{0.05cm}$$

$$ \Rightarrow \hspace{0.3cm} A_2 \hspace{0.15cm}\underline {= 2\,{\rm V}},\hspace{0.5cm} A_4 \hspace{0.15cm}\underline {= 1.936\,{\rm V}}.$$

Unter Berücksichtigung des nachfolgenden Tiefpassfilters kann hierfür auch geschrieben werden:

$$ v(t) = A_2 \cdot \cos( \omega_{\rm 2} \cdot (t - \tau_2))+ A_4 \cdot \cos( \omega_{\rm 4} \cdot (t - \tau_4))\hspace{0.05cm}.$$

Die Amplituden sind gegenüber Teilaufgabe d) unverändert. Für die Laufzeiten erhält man mit $Δϕ_T = π/6$:

$$ \tau_2 = \frac {\Delta \phi_{\rm T}}{2 \pi \cdot f_2} = \frac {\pi /6}{2 \pi \cdot 2\,{\rm kHz}} \hspace{0.15cm}\underline {\approx 41.6\,{\rm \mu s}},\hspace{0.5cm} \tau_4 = \frac {\Delta \phi_{\rm T}}{2 \pi \cdot f_4}= \frac {\tau_2}{2}\hspace{0.15cm}\underline {\approx 20.8\,{\rm \mu s}} \hspace{0.05cm}.$$

(6)  Richtig sind der erste und der letzte Lösungsvorschlag:

• Auch bei ESB führen Dämpfungsverzerrungen auf dem Kanal ausschließlich zu Dämpfungsverzerrungen bezüglich $v(t)$.
• Phasenverzerrungen gibt es nur bei einem Demodulator mit Phasenversatz, wenn eine Einseitenbandmodulation Anwendung findet.
• Bei der ZSB–AM hätte ein solcher Phasenversatz keine Verzerrungen zur Folge, sondern lediglich eine frequenzunabhängige Dämpfung.
• Zu Phasenverzerrungen bezüglich $v(t)$ kommt es bei der ZSB–AM und der ESB–AM auch, wenn solche bereits auf dem Kanal auftreten.