Aufgaben:Aufgabe 3.4: Einfacher Phasenmodulator

• Zurück zum Buch

„Näherungsweiser Phasenmodulator”

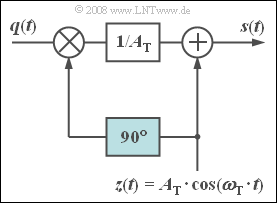
Die nebenstehende Schaltung erlaubt die näherungsweise Realisierung eines phasenmodulierten Signals. Der $90^\circ$–Phasenschieber formt aus dem cosinusförmigen Träger $z(t)$ ein Sinussignal gleicher Frequenz, so dass für das modulierte Signal geschrieben werden kann:

$$ s(t) = z(t) + q(t) \cdot \frac{z(t- T_0/4)}{A_{\rm T}} = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t) + q(t) \cdot \sin (\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$

Der zweite Term beschreibt eine „ZSB–AM ohne Träger”. Zusätzlich wird der um $90^\circ$ phasenverschobene Träger addiert. Bei cosinusförmigem Quellensignal $q(t) = A_{\rm N} \cdot \cos (\omega_{\rm N} \cdot t)$ergibt sich somit:

$$s(t) = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t) + A_{\rm N} \cdot \cos (\omega_{\rm N} \cdot t) \cdot \sin (\omega_{\rm T} \cdot t) $$

$$\Rightarrow \hspace{0.3cm}s(t) = A_{\rm T} \cdot \left[\cos (\omega_{\rm T} \cdot t) + \eta \cdot \cos (\omega_{\rm N} \cdot t) \cdot \sin (\omega_{\rm T} \cdot t) \right] \hspace{0.05cm}.$$

Das Verhältnis $η = A_{\rm N}/A_{\rm T}$ bezeichnen wir als den Modulationsindex; die Trägeramplitude wird im Folgenden zur Vereinfachung $A_{\rm T} = 1$ gesetzt.

• Im Gegensatz zur idealen Phasenmodulation unterscheidet sich bei dieser „näherungsweisen Phasenmodulation” $η$ vom Phasenhub $ϕ_{\rm max}$.
• Außerdem werden Sie erkennen, dass die Hüllkurve $a(t) ≠ 1$ ist. Das bedeutet, dass hier der Phasenmodulation eine unerwünschte Amplitudenmodulation überlagert ist.

Berechnet werden sollen in dieser Aufgabe aus der Darstellung des äquivalenten TP–Signals $s_{TP}(t)$ in der komplexen Ebene (Ortskurve)

• die Hüllkurve $a(t)$ und
• die Phasenfunktion $ϕ(t)$.

Anschließend sollen die Verfälschungen analysiert werden, die sich ergeben, wenn bei diesem nichtidealen PM-Modulator empfangsseitig ein idealer PM-Demodulator eingesetzt wird, der das Sinkensignal $v(t)$ proportional zur Phase $ϕ(t)$ setzt.

Hinweise:

• Die Aufgabe gehört zum Kapitel Phasenmodulation.
• Bezug genommen wird insbesondere auf die Seite Äquivalentes Tiefpass-Signal bei Phasenmodulation.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Zur näherungsweisen Berechnung des Klirrfaktors können Sie folgende Gleichungen benutzen:

$$\arctan(\gamma) \approx \gamma - {\gamma^3}/{3} \hspace{0.05cm}, \hspace{0.3cm} \cos^3(\gamma) ={3}/{4} \cdot \cos(\gamma) +{1}/{4} \cdot \cos(3 \cdot \gamma) \hspace{0.05cm}.$$

Fragebogen

1

Berechnen Sie das äquivalente Tiefpass–Signal. Welche Aussage trifft zu?

	Die Ortskurve $s_{\rm TP}(t)$ ist ein Kreisbogen.
	Die Ortskurve $s_{\rm TP}(t)$ ist eine horizontale Gerade.
	Die Ortskurve $s_{\rm TP}(t)$ ist eine vertikale Gerade.

2

Berechnen Sie die (normierte) Hüllkurve $a(t)$ für $A_{\rm T} = 1$. Wie groß sind deren Minimal– und Maximalwert mit $η = 1$?

$a_{\rm min} \ = \ $

$a_{\rm max} \ = \ $

3

Berechnen Sie den Maximalwert der Phase $ϕ(t)$ für $η = 1$ und $η = 0.5$.

$η = 1.0\text{:} \ \ \ ϕ_{\rm max} \ = \ $ $\ \rm Grad$

$η = 0.5\text{:} \ \ \ ϕ_{\rm max} \ = \ $ $\ \rm Grad$

4

Welche Verzerrungen ergeben sich nach idealer Phasendemodulation von $s(t)$?

	Es treten keine Verzerrungen auf.
	Es treten lineare Verzerrungen auf.
	Es treten nichtlineare Verzerrungen auf.

5

Berechnen Sie den Klirrfaktor $K$ unter Berücksichtigung der auf der Angabenseite genannten trigonometrischen Beziehungen.

$η = 1.0\text{:} \ \ \ K \ = \ $ $\ \text{%}$

$η = 0.5\text{:} \ \ \ K \ = \ $ $\ \text{%}$

Musterlösung

Musterlösung

Konstruktion der „vertikalen” Ortskurve aus den Zeigern

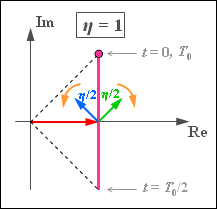
(1)  Richtig ist der Lösungsvorschlag 3:

• Das äquivalente Tiefpass–Signal lautet:

$$s_{\rm TP}(t) = A_{\rm T} \cdot \left ( 1 + {\rm j}\cdot \frac {\eta}{2}\cdot \left ({\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t} + {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}\right) \right) = A_{\rm T} \cdot \left ( 1 + {\rm j}\cdot {\eta}\cdot \cos (\omega_{\rm N} \cdot t) \right)\hspace{0.05cm}.$$

• Die Grafik verdeutlicht, dass die Ortskurve $s_{\rm TP}(t)$ nun eine vertikale Gerade ist im Gegensatz zur idealen PM (Kreisbogen) und zur ZSB–AM (horizontale Gerade). Im Folgenden wird $A_{\rm T} = 1$ gesetzt.

(2)  Die Hüllkurve ergibt sich aus der zeitabhängigen Zeigerlänge zu

$$a(t) = \sqrt{1 + \eta^2 \cdot \cos^2 (\omega_{\rm N} \cdot t)} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}a_{\rm min} \hspace{0.15cm}\underline { = 1}, \hspace{0.3cm}a_{\rm max} = \sqrt{1 + \eta^2 }\hspace{0.05cm}.$$

Für $η = 1$ ergibt sich der Maximalwert zu $a_{\rm max} = \sqrt{2}\hspace{0.15cm}\underline { ≈ 1.414}$.

(3)  Für die Phasenfunktion dieses einfachen Phasendemodulators gilt:

$$\phi(t) = \arctan \frac{{\rm Im}[s_{\rm TP}(t)]}{{\rm Re}[s_{\rm TP}(t)]} = \arctan (\eta \cdot \cos (\omega_{\rm N} \cdot t)) \hspace{0.05cm}.$$

Der Maximalwert tritt beispielsweise zur Zeit $t = 0$ auf und beträgt $ϕ_{\rm max} = \arctan(η)$.

• Für $η = 1$ erhält man $ϕ_{\rm max}\hspace{0.15cm}\underline { = 45^\circ}$ (im Vergleich: Bei idealer PM $57.3^\circ$),
• Für $η = 0.5$ergibt sich $ϕ_{\rm max}\hspace{0.15cm}\underline { \approx 26.6^\circ}$ (bei idealer PM $28.7^\circ$).

(4)  Richtig ist der Lösungsvorschlag 3:

• Es gilt nicht $\arctan[η · cos(γ)] = η · \cos(γ)$.
• Das heißt, dass das Sinkensignal im Gegensatz zum Quellensignal nicht cosinusförmig verläuft.
• Dies weist auf nichtlineare Verzerrungen hin.

(5)  Mit $γ = η · \cos(ω_N · t)$ und $\arctan(γ) ≈ γ – γ^3/3$ erhält man:

$$ \phi(t) = \eta \cdot \cos (\omega_{\rm N} \cdot t) - \frac{\eta^3}{3}\cdot \cos^3 (\omega_{\rm N} \cdot t))= \eta \cdot \cos (\omega_{\rm N} \cdot t) - \frac{\eta^3}{3}\cdot \left [ {3}/{4}\cdot \cos (\omega_{\rm N} \cdot t) + {1}/{4}\cdot \cos (3 \omega_{\rm N} \cdot t)\right ] $$

$$\Rightarrow \hspace{0.3cm} \phi(t) = \left(\eta - {\eta^3}/{4} \right) \cdot \cos (\omega_{\rm N} \cdot t) - {\eta^3}/{12}\cdot \cos (3\omega_{\rm N} \cdot t)) \hspace{0.05cm}.$$

Das bedeutet: Bei Verwendung der angegebenen Reihenentwicklung (Terme 5. und höherer Ordnung werden vernachlässigt) ist nur der Klirrfaktor dritter Ordnung von $0$ verschieden. Man erhält:

$$K = K_3 = \frac{\eta^3/12}{\eta-\eta^3/4}= \frac{1}{12/\eta^2 -3} \hspace{0.05cm}.$$

• Für $η = 1$ ergibt sich der Zahlenwert $K = 1/9 \hspace{0.15cm}\underline { ≈ 11.1\%}$.
• Für $η = 0.5$ ist der Klirrfaktor $K = 1/45 \hspace{0.15cm}\underline {≈ 2.2\%}$.

Eine Simulation zeigt, dass man durch den Abbruch der Reihe nach dem Term dritter Ordnung einen Fehler macht, der den Klirrfaktor als zu hoch erscheinen lässt:

• Die per Simulation gewonnenen Werte sind $K ≈ 6%$ (für $η = 1$) und $K ≈ 2%$ (für $η = 0.5$).
• Der Fehler nimmt also mit wachsendem η mehr als proportional zu.