Aufgaben:Aufgabe 4.8Z: BPSK–Fehlerwahrscheinlichkeit

• Zurück zum Buch

Tabelle der Komplementären Gaußschen Fehlerfunktion Q(x)

Wir gehen von dem optimalen Basisbandübertragungssystem für Binärsignale aus mit

• bipolaren Amplitudenkoeffizienten $a_ν ∈ \{-1, +1\}$,
• rechteckförmigem Sendesignal mit den Signalwerten $±s_0$ und der Bitdauer $T_{\rm B}$,
• AWGN–Rauschen mit der Rauschleistungsdichte $N_0$,
• Empfangsfilter gemäß dem Matched–Filter–Prinzip,
• Entscheider mit optimalem Schwellenwert $E = 0$.

Wenn nichts anderes angegeben ist, so sollten Sie von den folgenden Zahlenwerten ausgehen:

$$s_0 = 4\,{\rm V},\hspace{0.2cm} T_{\rm B} = 1\,{\rm ns},\hspace{0.2cm}N_0 = 2 \cdot 10^{-9}\, {\rm V^2/Hz} \hspace{0.05cm}.$$

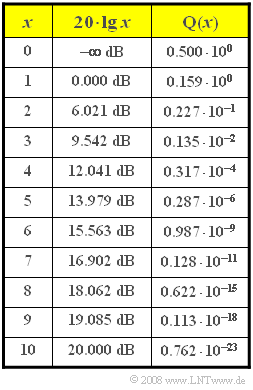
Die Bitfehlerwahrscheinlichkeit dieses Basisbandsystems lautet mit dem Rauscheffektivwert $σ_d$ am Entscheider und der komplementären Gaußschen Fehlerfunktion ${\rm Q}(x)$   ⇒   siehe Tabelle:

$$ p_{\rm BB} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}.$$

Diese Bitfehlerwahrscheinlichkeit kann auch in der Form

$$p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right )$$

geschrieben werden, wobei $E_{\rm B}$ die „Signalenergie pro Bit” angibt.

Die Bitfehlerwahrscheinlichkeit eines vergleichbaren Übertragungssystems mit Binary Phase Shift Keying (BPSK) lautet:

$$ p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/{T_{\rm B}}}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Lineare digitale Modulation.
• Bezug genommen wird insbesondere auf die Seite Fehlerwahrscheinlichkeiten - ein kurzer Überblick.
• Die Herleitungen finden Sie im Kapitel Lineare digitale Modulation – Kohärente Demodulation des Buches „Digitalsignalübertragung”.
• Die Angabe einer Leistung in $\rm V^2$ bzw. einer Energie in $\rm V^2 s$ bedeutet eine Umrechnung auf den Bezugswiderstand $1 \ \rm \Omega$.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

$s_0 = 4\,{\rm V},\hspace{0.2cm} T_{\rm B} = 1\,{\rm ns},\hspace{0.2cm}N_0 = 2 \cdot 10^{-9}\, {\rm V^2/Hz} \hspace{0.05cm}.$ Wie groß ist die Fehlerwahrscheinlichkeit $p_{\rm BB}$ des Basisbandsystems?

$p_{\rm BB} \ = \ $ $\ \cdot 10^{-4}$

2

Wie groß ist für diesen Parametersatz die Energie pro Bit   ⇒   $E_{\rm B}$ beim Basisbandsystem?

$E_{\rm B} \ = \ $ $\ \cdot 10^{-8} \ \rm V^2 s$

3

Welche Fehlerwahrscheinlichkeit ergibt sich bei halber Sendeamplitude   ⇒   $s_0 = 2\,{\rm V}$?

$p_{\rm BB} \ = \ $ $\ \cdot 10^{-4}$

4

Geben Sie die Fehlerwahrscheinlichkeit der BPSK abhängig vom Quotienten $E_{\rm B}/N_0$ an. Welches Ergebnis stimmt?

	$p_{\rm BPSK} = {\rm Q}[(E_{\rm B}/N_0)^{1/2}],$
	$p_{\rm BPSK} = {\rm Q}[(2E_{\rm B}/N_0)^{1/2}],$
	$p_{\rm BPSK} = {\rm Q}[(4E_{\rm B}/N_0)^{1/2}].$

5

Welche Fehlerwahrscheinlichkeiten ergeben sich bei der BPSK für $E_{\rm B}/N_0 = 8$ und $E_{\rm B}/N_0 = 2$?

$E_{\rm B}/N_0 = 8\text{:} \ \ p_{\rm BPSK} \ = \ $ $\ \cdot 10^{-4}$

$E_{\rm B}/N_0 = 2\text{:} \ \ p_{\rm BPSK} \ = \ $ $\ \cdot 10^{-4}$

Musterlösung

Musterlösung

(1)  Der Rauscheffektivwert ergibt sich hier zu

$$\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}= \sqrt{\frac{2 \cdot 10^{-9}\,{\rm V^2/Hz}}{2 \cdot 1\,{\rm ns}}}= 1\,{\rm V} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm BB} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )= {\rm Q}(4)\hspace{0.15cm}\underline {= 0.317 \cdot 10^{-4}}.$$

(2)  Beim Basisbandsystem gilt:

$$E_{\rm B} = s_0^2 \cdot T_{\rm B}= (4\,{\rm V})^2 \cdot 10^{-9}\,{\rm s}\hspace{0.15cm}\underline {= 1.6 \cdot 10^{-8}\,{\rm V^2s}}.$$

Natürlich ergibt sich mit der zweiten angegebenen Gleichung die genau gleiche Fehlerwahrscheinlichkeit

$$ p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 16 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$

(3)  Bei halber Sendeamplitude $s_0 = 2\,{\rm V}$ sinkt die Energie pro Bit auf ein Viertel und es gelten folgende Gleichungen:

$$ p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \frac{2\,{\rm V}}{1\,{\rm V}} \right )= {\rm Q}(2)= 227 \cdot 10^{-4},$$

$$ p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 4 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(2)\hspace{0.15cm}\underline {= 227 \cdot 10^{-4}}.$$

(4)  Richtig ist die Antwort 2:

• Unter Berücksichtigung der Energie $E_{\rm B} = s_0^2 · T_{\rm B}/2$ erhält man

$$ p_{\rm BPSK} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }}\hspace{0.1cm}\right ).$$

• Man erhält somit das gleiche Ergebnis wie beim optimalen Basisbandübertragungssystem.

(5)  Es ergeben sich die genau gleichen Ergebnisse wie bei der Basisbandübertragung in den Teilaufgaben (1) und (3):

$${ E_{\rm B}}/{N_0 }= 8: \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{16}) = {\rm Q}(4)\hspace{0.15cm}\underline {= 0.317 \cdot 10^{-4}},$$

$$ { E_{\rm B}}/{N_0 }= 2: \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{4}) = {\rm Q}(2)\hspace{0.15cm}\underline {= 227 \cdot 10^{-4}}.$$