Modulationsverfahren/Fehlerwahrscheinlichkeit der PN–Modulation: Unterschied zwischen den Versionen
| Zeile 58: | Zeile 58: | ||
==Asynchroner CDMA–Betrieb mit Walsh–Funktionen== | ==Asynchroner CDMA–Betrieb mit Walsh–Funktionen== | ||
| − | + | Auf der Seite [[Modulationsverfahren/Fehlerwahrscheinlichkeit_der_PN–Modulation#Systemkonfigurationen_f.C3.BCr_minimale_Fehlerwahrscheinlichkeit|Systemkonfigurationen für minimaleFehlerwahrscheinlichkeit]] wurde gezeigt, dass bei Verwendung von orthogonalen Walsh–Funktionen die Bitfehlerwahrscheinlichkeit $p_{\rm B}$ auch bei Vorhandensein anderer CDMA–Teilnehmer gegenüber der BPSK–Vergleichskurve (System ohne Bandspreizung) nicht verändert wird, so lange alle Teilnehmer synchron arbeiten. | |
| + | *Diese Voraussetzung ist im Mobilfunk im allgemeinen für den Downlink (der Sender ist eine einzige Basisstation) erfüllt, | ||
| + | *nicht jedoch im Uplink (Sender sind viele mobile Endgeräte). | ||
| − | [[Datei:P_ID1897__Mod_T_5_4_S4_neu.png | | + | [[Datei:P_ID1897__Mod_T_5_4_S4_neu.png |center|frame| Bitfehlerwahrscheinlichkeit bei asynchronem CDMA–Betrieb mit Walsh-Spreizfunktionen]] |
| + | Die Grafik zeigt die Bitfehlerwahrscheinlichkeitskurven für den jeweils ungünstigsten Phasenversatz der Spreizfolgen von betrachtetem Teilnehmer und störendem Teilnehmer, jeweils mit Spreizgrad $J = 16$. Der erste Teilnehmer benutze dabei stets die Walsh–Funktion Nr. 15. Das Ergebnis kann wie folgt zusammengefasst werden: | ||
| + | *Benutzt der störende Teilnehmer die Walsh–Funktion Nr. 1, so macht sich ein Phasenversatz nicht negativ bemerkbar, da für alle $λ$–Werte die PKKF $φ_\text{1, 15}(λ · T_c) = 0$ ist. | ||
| + | *Verwendet dagegen der zweite Teilnehmer die Walsh–Funktion Nr. 14 (oder jede andere mit der Kenn-Nummer größer/gleich 8), so ergibt sich durch einen Phasenversatz um eine Chipdauer eine enorme Verschlechterung. Es gilt zwar $φ_\text{14, 15}(0) = 0$, aber für $λ = 1$ hat diese PKKF mit $φ_\text{14, 15}(T_c) = 3/4$ einen sehr großen Wert. | ||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Bitfehlerwahrscheinlichkeit beim Zweiwegekanal== |
| − | Für den Rest | + | Für den Rest dieses Kapitels „Fehlerwahrscheinlichkeit der PN–Modulation” setzen wir voraus: |
| − | $$h_{\rm K}(t) = 0.8 \cdot \delta (t) + 0.6 \cdot \delta (t - 2 T_c)$$ | + | *Zur Bandspreizung werden Walsh–Funktionen verwendet. Der Spreizfaktor ist jeweils $J = 16$. Insbesondere betrachten wir die Funktionen: |
| − | Das heißt: Der Hauptpfad wird um den Faktor 0.8 gedämpft. Daneben gibt es ein Echo im Abstand $2T_c$ mit dem Gewicht 0.6 | + | :$$ \langle w_\nu^{\hspace{0.12cm}(1)}\rangle = |
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.05cm},$$ | ||
| + | :$$ \langle w_\nu^{\hspace{0.12cm}(2)}\rangle = | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.05cm},$$ | ||
| + | :$$ \langle w_\nu^{(12)}\rangle = | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {-\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1} \hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1}\hspace{0.15cm} | ||
| + | {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$ | ||
| + | *Aktiv ist jeweils nur ein Teilnehmer ⇒ Interferenzen durch andere Nutzer treten nicht auf. | ||
| + | *Der Kanal enthält neben dem AWGN–Rauschen noch eine Mehrwegekomponente enthält. Die Kanalimpulsantwort lautet: | ||
| + | :$$h_{\rm K}(t) = 0.8 \cdot \delta (t) + 0.6 \cdot \delta (t - 2 T_c)$$ | ||
| + | :Das heißt: Der Hauptpfad wird um den Faktor $0.8$ gedämpft. Daneben gibt es ein Echo im Abstand $2T_c$ mit dem Gewicht $0.6$. | ||
| + | [[Datei:P_ID1898__Mod_T_5_4_S5a_neu.png |center|frame| CDMA–Fehlerwahrscheinlichkeit beim Zweiwegekanal]] | ||
| − | + | Die Grafik zeigt Bitfehlerwahrscheinlichkeitskurven. Diese zeigen folgende Sachverhalte: | |
| − | |||
| − | |||
| − | |||
*Die Walsh–Funktion Nr. 2 (+ + – – + + – – ...) ist für den oben definierten Zweiwegekanalanal denkbar ungeeignet, da sich hier das bandgespreizte Signal $b(t)$ aufgrund des Echos im Abstand $2T_c$ nahezu auslöscht. Dies erkennt man auch am PAKF–Wert $φ_{22}(τ = 2T_c) =$ –1. | *Die Walsh–Funktion Nr. 2 (+ + – – + + – – ...) ist für den oben definierten Zweiwegekanalanal denkbar ungeeignet, da sich hier das bandgespreizte Signal $b(t)$ aufgrund des Echos im Abstand $2T_c$ nahezu auslöscht. Dies erkennt man auch am PAKF–Wert $φ_{22}(τ = 2T_c) =$ –1. | ||
*Die Walsh–Funktion Nr. 1 (+ – + – + – + – ...) ist dagegen bei diesem Kanal sehr gut geeignet. Das Echosignal überlagert sich dem Signal auf dem Hauptfeld konstruktiv und $b(t)$ wird fast verdoppelt. Das sehr gute Ergebnis lässt sich durch den PAKF–Wert $φ_{11}(τ = 2T_c) =$ +1 erklären. | *Die Walsh–Funktion Nr. 1 (+ – + – + – + – ...) ist dagegen bei diesem Kanal sehr gut geeignet. Das Echosignal überlagert sich dem Signal auf dem Hauptfeld konstruktiv und $b(t)$ wird fast verdoppelt. Das sehr gute Ergebnis lässt sich durch den PAKF–Wert $φ_{11}(τ = 2T_c) =$ +1 erklären. | ||
Version vom 3. August 2017, 14:03 Uhr
Inhaltsverzeichnis
- 1 Das CDMA–System IS–95
- 2 Systemkonfigurationen für minimale Fehlerwahrscheinlichkeit
- 3 Zwei Teilnehmer mit M–Sequenz–Spreizung
- 4 Asynchroner CDMA–Betrieb mit Walsh–Funktionen
- 5 Bitfehlerwahrscheinlichkeit beim Zweiwegekanal
- 6 Fehlerwahrscheinlichkeit bei Zweiwegekanal (2)
- 7 Untersuchungen zum RAKE–Empfänger
- 8 Untersuchungen zum RAKE–Empfänger (2)
- 9 Quellenverzeichnis
Das CDMA–System IS–95
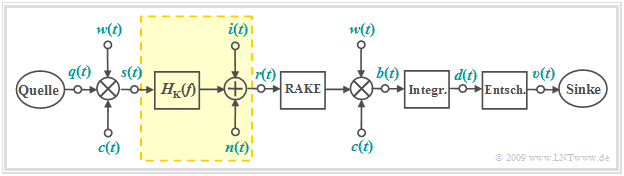
Die Eigenschaften der PN–Modulation sollen nun am Beispiel des amerikanischen Mobilfunkstandards IS–95, der sich aus den Arbeiten der Fa. Qualcomm Inc. und insbesondere von Andrew J. Viterbi ergeben hat, quantitativ angegeben werden. In etwas vereinfachter Darstellung – ohne Faltungscodierer, Interleaver und De–Interleaver sowie dem Viterbi–Decoder beim Empfänger – ergibt sich das folgende Blockschaltbild.
Es gelten folgende Aussagen:
- Das Spreizsignal $c(t)$ bewirkt eine Bandspreizung um den Spreizfaktor $J$, wobei auf den nächsten Seiten sowohl Walsh–Funktionen als auch M–Sequenzen betrachtet werden. Die Bandstauchung beim Empfänger benutzt phasensynchron die gleiche Spreizfolge.
- Das zusätzliche $±1$–Signal $w(t)$ ermöglicht eine zusätzliche Verwürfelung, bewirkt jedoch keine weitere Bandspreizung. Die Rechteckdauer von $w(t)$ ist genau so groß wie die Rechteckdauer von $c(t)$. Man nennt $T_c$ die Chipdauer.
- Ohne Bandspreizung und Verwürfelung (bzw. mit $J = 1$) entspricht die Übertragungskette der BPSK–Modulation. Das Matched–Filter ist durch die Variante Integrate & Dump realisiert, so dass es sich um ein optimales System handelt.
- Mit $H_{\rm K}(f) = 1$ ergibt sich das Modulationsverfahren/Qualitätskriterien mit dem gaußverteilten Rauschsignal $n(t)$ und der AWGN–Kenngröße $E_{\rm B}/N_0$. Die zusätzliche Störkomponente $i(t)$ fasst die Interferenzen der anderen Teilnehmer zusammen.
- Bei einem Mehrwegekanal (ein Hauptpfad und ein oder mehrere Nebenpfade) können die entstehenden Impulsinterferenzen durch den Einsatz eines RAKE–Empfängers vermindert werden.
Alle nachfolgenden Ergebnisse wurden mit dem Simulationsprogramm „CDMA” ermittelt. Dieses wurde an der TU München im Praktikum „Simulation digitaler Übertragungssysteme” [Söd01][1] eingesetzt. Dieser Versuch basiert auf
- der Lehrsoftware CDMA ⇒ Link verweist auf die ZIP-Version des Programms und
- der zugehörigen Praktikumsanleitung ⇒ Link verweist auf die PDF-Version.
Systemkonfigurationen für minimale Fehlerwahrscheinlichkeit
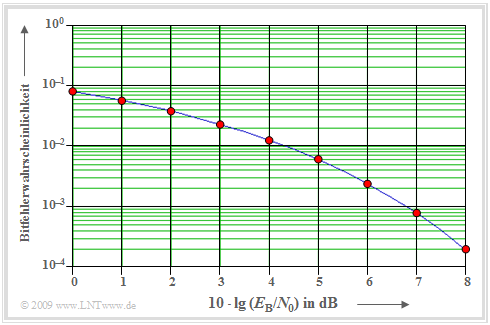
Die Grafik zeigt als durchgezogene blaue Kurve die Bitfehlerwahrscheinlichkeit bei BPSK in Abhängigkeit des logarithmierten AWGN–Parameters $E_{\rm B}/N_0$ (Signalenergie pro Bit bezogen auf die Rauschleistungsdichte). Es gilt mit der komplementären Gaußschen Fehlerfunktion ${\rm Q}(x)$:
- $$p_{\rm B} = {\rm Q} \left ( \sqrt{{2E_{\rm B}}/{N_{\rm 0}}}\hspace{0.05cm}\right ) \hspace{0.05cm}.$$
Beispielsweise ergibt sich für $10 · \lg \ (E_{\rm B}/N_0) = 8 \ \rm dB$ näherungsweise die Bitfehlerwahrscheinlichkeit $p_{\rm B} = \rm 2 · 10^{–4}$.
Den gleichen minimalen Wert liefert eine Simulation (rote Punkte) unter folgenden Bedingungen:
- PN–Modulation, egal ob mit einer M–Sequenz oder mit einer Walsh–Funktion, bei beliebigem Spreizgrad $J$, falls nur ein Teilnehmer aktiv ist;
- synchroner CDMA–Betrieb mit Walsh–Funktionen, auch wenn im gleichen Frequenzband andere Nutzer (maximal $J -1$) aktiv sind;
- auf den RAKE–Empfänger kann verzichtet werden, da beim AWGN–Kanal keine Impulsinterferenzen auftreten.
Zwei Teilnehmer mit M–Sequenz–Spreizung
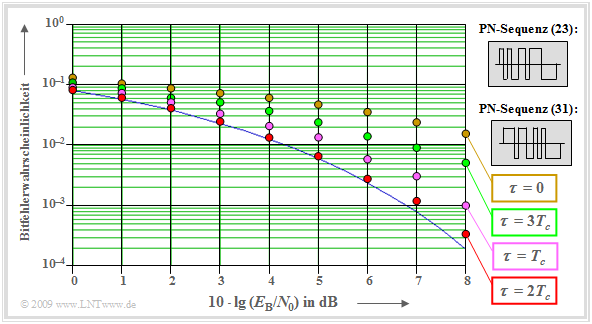
Wir betrachten den störenden Einfluss eines zweiten Teilnehmers auf die Fehlerwahrscheinlichkeit von Teilnehmer 1.
- Die Spreizung erfolgt mittels M–Sequenzen, die im Gegensatz zu den Walsh–Funktionen nicht zueinander orthogonal sind.
- Weiter gilt der Spreizfaktor $J = 15$. Die Oktalkennungen der PN–Spreizfolgen seien (23) und (31).
- Bei nur einem Teilnehmer ergibt sich die blaue durchgezogene Kurve. Der zweite (taktsynchrone) Teilnehmer erhöht die Fehlerwahrscheinlichkeit gravierend, zum Beispiel für $10 · \lg \ (E_{\rm B}/N_0) = 8 \ \rm dB$ von $p_{\rm B} = 0.02\%$ auf $p_{\rm B} =1.5\%$ (braune Markierungen, $τ = 0$).
- Durch einen Phasenversatz der PN–Sequenzen gegeneinander um Vielfache der Chipdauer kann man beträchtliche Verbesserungen erzielen. Verschiebt man beispielsweise die PN–Sequenz (31) des interferierenden Teilnehmers um $τ = 2T_c$ nach rechts (rote Markierungen), so erhält man statt $1.5\%$ Fehler nur mehr die Fehlerwahrscheinlichkeit $p_{\rm B} = 0.034\%$.
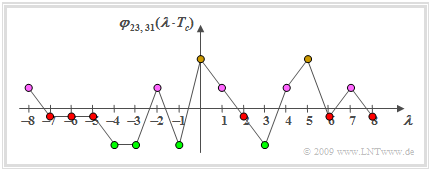
Die Ergebnisse werden verständlich, wenn man die periodische KKF $φ_\text{23, 31}(λ \cdot T_c)$ zwischen den Sequenzen (23) und (31) betrachtet.
- Je kleiner der PKKF–Betrag ist, desto kleiner wird $p_{\rm B}$.
- Man könnte also auch die zweite PN–Sequenz um sechs oder acht Chipdauern nach rechts oder um fünf, sechs oder sieben Chipdauern nach links verschieben.
- In all diesen Fällen ist der PKKF–Betrag$|φ_\text{23, 31}(2 T_c)| = 1/15$ (rote Punkte) kleiner im Vergleich zu
- $|φ_\text{23, 31}(0)| = 7/15$ (ockerfarbene Punkte) ,
- $|φ_\text{23, 31}(3 T_c)| = 5/15$ (grüne Punkte) sowie
- $|φ_\text{23, 31}(T_c)| = 3/15$ (violette Punkte).
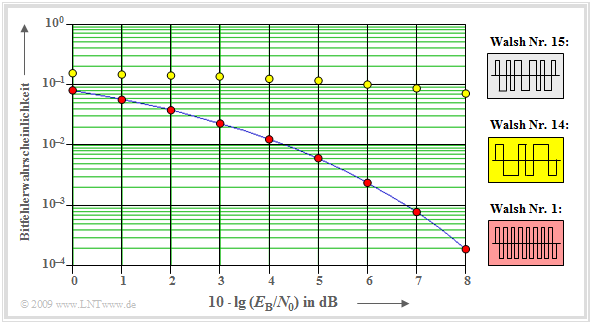
Asynchroner CDMA–Betrieb mit Walsh–Funktionen
Auf der Seite Systemkonfigurationen für minimaleFehlerwahrscheinlichkeit wurde gezeigt, dass bei Verwendung von orthogonalen Walsh–Funktionen die Bitfehlerwahrscheinlichkeit $p_{\rm B}$ auch bei Vorhandensein anderer CDMA–Teilnehmer gegenüber der BPSK–Vergleichskurve (System ohne Bandspreizung) nicht verändert wird, so lange alle Teilnehmer synchron arbeiten.
- Diese Voraussetzung ist im Mobilfunk im allgemeinen für den Downlink (der Sender ist eine einzige Basisstation) erfüllt,
- nicht jedoch im Uplink (Sender sind viele mobile Endgeräte).
Die Grafik zeigt die Bitfehlerwahrscheinlichkeitskurven für den jeweils ungünstigsten Phasenversatz der Spreizfolgen von betrachtetem Teilnehmer und störendem Teilnehmer, jeweils mit Spreizgrad $J = 16$. Der erste Teilnehmer benutze dabei stets die Walsh–Funktion Nr. 15. Das Ergebnis kann wie folgt zusammengefasst werden:
- Benutzt der störende Teilnehmer die Walsh–Funktion Nr. 1, so macht sich ein Phasenversatz nicht negativ bemerkbar, da für alle $λ$–Werte die PKKF $φ_\text{1, 15}(λ · T_c) = 0$ ist.
- Verwendet dagegen der zweite Teilnehmer die Walsh–Funktion Nr. 14 (oder jede andere mit der Kenn-Nummer größer/gleich 8), so ergibt sich durch einen Phasenversatz um eine Chipdauer eine enorme Verschlechterung. Es gilt zwar $φ_\text{14, 15}(0) = 0$, aber für $λ = 1$ hat diese PKKF mit $φ_\text{14, 15}(T_c) = 3/4$ einen sehr großen Wert.
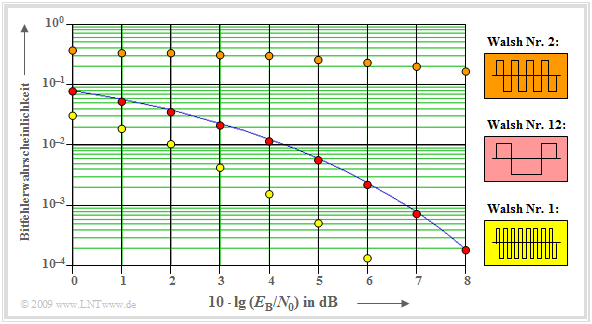
Bitfehlerwahrscheinlichkeit beim Zweiwegekanal
Für den Rest dieses Kapitels „Fehlerwahrscheinlichkeit der PN–Modulation” setzen wir voraus:
- Zur Bandspreizung werden Walsh–Funktionen verwendet. Der Spreizfaktor ist jeweils $J = 16$. Insbesondere betrachten wir die Funktionen:
- $$ \langle w_\nu^{\hspace{0.12cm}(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$
- $$ \langle w_\nu^{\hspace{0.12cm}(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$
- $$ \langle w_\nu^{(12)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$
- Aktiv ist jeweils nur ein Teilnehmer ⇒ Interferenzen durch andere Nutzer treten nicht auf.
- Der Kanal enthält neben dem AWGN–Rauschen noch eine Mehrwegekomponente enthält. Die Kanalimpulsantwort lautet:
- $$h_{\rm K}(t) = 0.8 \cdot \delta (t) + 0.6 \cdot \delta (t - 2 T_c)$$
- Das heißt: Der Hauptpfad wird um den Faktor $0.8$ gedämpft. Daneben gibt es ein Echo im Abstand $2T_c$ mit dem Gewicht $0.6$.
Die Grafik zeigt Bitfehlerwahrscheinlichkeitskurven. Diese zeigen folgende Sachverhalte:
- Die Walsh–Funktion Nr. 2 (+ + – – + + – – ...) ist für den oben definierten Zweiwegekanalanal denkbar ungeeignet, da sich hier das bandgespreizte Signal $b(t)$ aufgrund des Echos im Abstand $2T_c$ nahezu auslöscht. Dies erkennt man auch am PAKF–Wert $φ_{22}(τ = 2T_c) =$ –1.
- Die Walsh–Funktion Nr. 1 (+ – + – + – + – ...) ist dagegen bei diesem Kanal sehr gut geeignet. Das Echosignal überlagert sich dem Signal auf dem Hauptfeld konstruktiv und $b(t)$ wird fast verdoppelt. Das sehr gute Ergebnis lässt sich durch den PAKF–Wert $φ_{11}(τ = 2T_c) =$ +1 erklären.
- Für die Walsh–Funktion Nr. 12 gleichen sich die konstruktiven und destruktiven Überlagerungen nahezu aus, so dass die Fehlerwahrscheinlichkeit in etwa auf der BPSK–Kurve zu liegen kommt. Auch alle anderen Walsh–Funktionen liegen zwischen den braunen und gelben Grenzkurven.
Da aber ein Netzbetreiber für alle Teilnehmer gleiche Bedingungen bereitstellen muss und sich die Grafik ausschließlich auf den oben angegebenen Kanal bezieht (zum Beispiel ist bei einer Echoverzögerung um $T_c$ die Walsh–Funktion Nr. 2 deutlich besser als Nr. 1), ist die hier betrachtete Konfiguration für den praktischen Betrieb ungeeignet. Nachfolgend wird gezeigt, wie man für alle Teilnehmer annähernd gleiche Bedingungen schaffen kann.
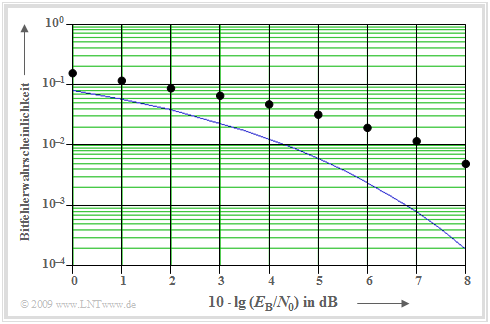
Fehlerwahrscheinlichkeit bei Zweiwegekanal (2)
Eine Möglichkeit, die Qualität für die einzelnen Benutzer (unterschiedliche Walsh–Funktionen, hier alle mit Spreizfaktor $J =$ 16) auch beim Zweiwegekanal zu egalisieren, bietet die zusätzliche Verwürfelung mit $w(t)$ entsprechend dem vorne gezeigten Blockschaltbild. Für die folgende Grafik ist für jeden Benutzer eine zusätzliche M–Sequenz der Periodenlänge $P =$ 63 (Grad $G =$ 6) vorausgesetzt.
Zu dieser Darstellung ist anzumerken:
- Die eingezeichneten Punkte gelten für die Walsh–Funktion Nr. 12 als Spreizsignal $c(t)$ und eine zusätzliche Verwürfelung $w(t)$ durch die M–Sequenz mit Oktalkennung (163).
- Die Ergebnisse für andere Walsh–Funktionen, zum Beispiel Nr. 1 oder Nr. 2 unterscheiden sich dem gegenüber innerhalb der Zeichengenauigkeit nur unwesentlich.
- Gegenüber dem reinen AWGN–Kanal (blaue Vergleichskurve) ergibt sich beim betrachteten Zweiwegekanal mit den Koeffizienten 0.8 und 0.6 eine Degradation von etwa 2 bis 3 dB.
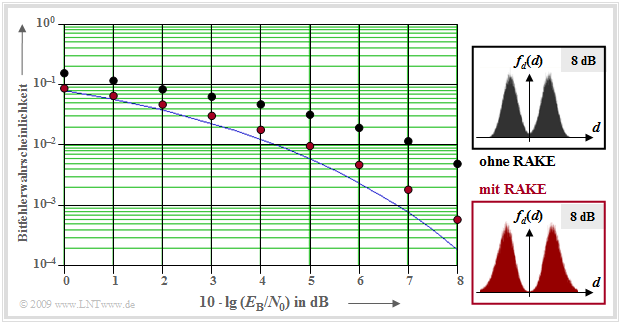
Untersuchungen zum RAKE–Empfänger
Betrachten wir abschließend die Verbesserung durch die Verwendung eines RAKE–Empfängers, die durch die nachfolgende Grafik verdeutlicht wird. Damit wird beispielsweise für 10 · lg $E_{\rm B}/N_0 =$ 8 dB die Bitfehlerwahrscheinlichkeit von $\rm 6 · 10^{–3}$ auf $\rm 5 · 10^{–4}$ herabgesetzt.
Der Grund für diese Verbesserung ist die kleinere Varianz ${σ_d}^2$ der Detektionsnutzabtastwerte, wie aus den rechts skizzierten Wahrscheinlichkeitsdichtefunktionen $f_d(d)$ hervorgeht (gültig für $E_{\rm B}/N_0 =$ 8 dB). Das kleinere $σ_d$ ist allein darauf zurückzuführen, dass der RAKE–Empfänger die Impulsinterferenzen bekämpft. Der Anteil des AWGN–Rauschens $n(t)$ an der Gesamtvarianz ${σ_d}^2$ (der zweite Anteil ist auf die Impulsinterferenzen zurückzuführen) hängt allein von der Abszisse $(E_{\rm B}/N_0)$ ab und ist mit und ohne RAKE gleich groß.
Anzumerken ist, dass für dieses Diagramm die genau gleichen Voraussetzungen gelten wie für die Grafik im letzten Abschnitt:
- Bandspreizung mit $J =$ 16 und Walsh–Funktion Nr. 12,
- zusätzliche Verwürfelung durch die M–Sequenz $\rm (163)_{oktal}$,
- Zweiwegekanal mit $h_{\rm K}(t) = 0.8 · δ(t) + 0.6 · δ(t – 2T_c)$.
Das Prinzip des RAKE–Empfängers wird im nächsten Abschnitt verdeutlicht.
Untersuchungen zum RAKE–Empfänger (2)
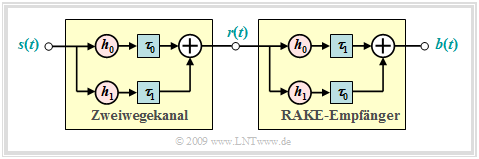
Das RAKE–Prinzip wird durch die nachfolgende Grafik verdeutlicht. Der Zweiwegekanal besteht aus
- dem direkten Pfad mit Verzögerungszeit $τ_0$ und Gewicht $h_0$,
- einem Echo mit Verzögerung $τ_1 > τ_0$ und Gewicht $h_1$.
Beide Amplitudenkoeffizienten seien reell. Als Normierungsbedingung gelte ${h_0}^2 + {h_1}^2 =$ 1.
Aufgabe des RAKE–Empfängers ist es, die Signalenergien der beiden Pfade (im allgemeinen: aller Pfade) auf einen einzigen Zeitpunkt zu konzentrieren. Er arbeitet demnach wie eine Harke für den Garten, was auch die deutsche Übersetzung für „RAKE” ist.
Legt man einen Diracimpuls zur Zeit $t =$ 0 an den Kanaleingang an ⇒ $s(t) = δ(t)$, so gibt es am Ausgang des RAKE–Empfängers drei Diracimpulse entsprechend der Gleichung $$b(t) = h_0 \cdot h_1\cdot \delta (t - 2 \tau_0) + (h_0^2 + h_1^2) \cdot \delta (t - \tau_0- \tau_1) + h_0 \cdot h_1\cdot \delta (t - 2 \tau_1) \hspace{0.05cm}.$$ Die Signalenergie konzentriert sich im Ausgangssignal auf den Zeitpunkt $τ_0 + τ_1$. Von den insgesamt vier Wegen tragen zwei dazu bei. Die Diracfunktionen bei $2τ_0$ und $2τ_1$ bewirken zwar Impulsinterferenzen. Ihre Gewichte $(h_0 · h_1)$ sind aber deutlich kleiner als das Gewicht des Hauptpfades $({h_0}^2 + {h_1}^2)$.
Mit den Kanalparametern $h_0 =$ 0.8 und $h_1 =$ 0.6 beinhaltet der Hauptpfad des Kanals (mit Gewicht $h_0$) nur $\rm 0.8^2/(0.8^2 + 0.6^2) = 64\%$ der gesamten Signalenergie. Mit RAKE–Empfänger und den gleichen Gewichten lautet die obige Gleichung $$b(t) =0.48 \cdot \delta (t - 2 \tau_0) + 1.0 \cdot \delta (t - \tau_0- \tau_1) + 0.48 \cdot \delta (t - 2 \tau_1) \hspace{0.05cm}.$$ Der Anteil des Hauptpfades an der Gesamtenergie beträgt nun $\rm 1^2/(1^2 + 0.48^2 + 0.48^2) ≈ 68\%$.
RAKE–Empfänger werden zur Implementierung in mobilen Geräten bevorzugt, haben aber bei vielen aktiven Teilnehmern nur eine begrenzte Leistungsfähigkeit. Bei einem Mehrwegekanal mit vielen ( $M$) Pfaden hat auch der RAKE $M$ Finger. Der Hauptfinger (Main Finger) – auch Searcher genannt – ist bei den meisten Mobilfunksystemen dafür verantwortlich, die individuellen Pfade der Mehrfachausbreitung zu identifizieren und einzuordnen.
Quellenverzeichnis
- ↑ Söder, G.: Simulation digitaler Übertragungssysteme. Anleitung zum gleichnamigen Praktikum. Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2001.