Aufgaben:Aufgabe 1.3Z: Nochmals Rayleigh–Fading?: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 3: | Zeile 3: | ||
[[Datei:P_ID2107__Mob_Z_1_3.png|right|frame]] | [[Datei:P_ID2107__Mob_Z_1_3.png|right|frame]] | ||
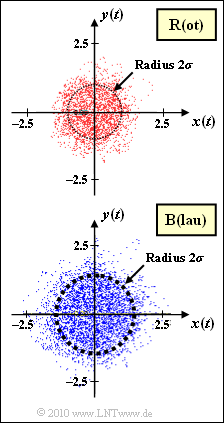
Dargestellt ist der multiplikative Faktor $z(t) = x(t) + j \cdot y(t)$ zweier Mobilfunkkanäle (beide ohne Mehrwegeausbreitung) in 2D–Darstellung. Als gesichert wird vorgegeben: | Dargestellt ist der multiplikative Faktor $z(t) = x(t) + j \cdot y(t)$ zweier Mobilfunkkanäle (beide ohne Mehrwegeausbreitung) in 2D–Darstellung. Als gesichert wird vorgegeben: | ||
| − | * Der Kanal R (die Bezeichnung ergibt sich aus der Farbe „Rot” der Punktwolke) ist rayleighverteilt mit $\ | + | * Der Kanal R (die Bezeichnung ergibt sich aus der Farbe „Rot” der Punktwolke) ist rayleighverteilt mit $\sigma_{\rm R} = 0.5$. |
| − | + | * Für die Wahrscheinlichkeitsdichtefunktion (WDF) von Betrag $a(t) = |z(t)|$ bzw. Betragsquadrat $p(t) = |z(t)|^2$ gelten somit die folgenden Gleichungen (mit $\sigma = \sigma_{\rm R}$): | |
| − | * Für die Wahrscheinlichkeitsdichtefunktion (WDF) von Betrag $a(t) = |z(t)|$ bzw. Betragsquadrat $p(t) = |z(t)|^2$ gelten somit die folgenden Gleichungen (mit $\sigma = \ | ||
:$$f_a(a) = | :$$f_a(a) = | ||
\left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm exp} [ -a^2/(2\sigma^2)] \\ | \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm exp} [ -a^2/(2\sigma^2)] \\ | ||
| Zeile 18: | Zeile 17: | ||
\\ {\rm f\ddot{u}r}\hspace{0.15cm} p < 0 \\ \end{array} | \\ {\rm f\ddot{u}r}\hspace{0.15cm} p < 0 \\ \end{array} | ||
.$$ | .$$ | ||
| − | + | * Vom Kanal B („Blau”) ist nur die Punktwolke gegeben. Es ist abzuschätzen, ob hier ebenfalls <i>Rayleigh–Fading</i> vorliegt, und wenn JA, wie groß bei diesem Kanal die Kenngröße $\sigma = \sigma_{\rm B}$ ist. | |
| − | * Vom Kanal B („Blau”) ist nur die Punktwolke gegeben. Es ist abzuschätzen, ob hier ebenfalls <i>Rayleigh–Fading</i> vorliegt, und wenn JA, wie groß bei diesem Kanal die Kenngröße $\sigma = \ | + | * In der Teilaufgabe 3) wird schließlich auch auf die WDF $f_{\it \phi}(\phi)$ der Phasenfunktion $\phi(t)$ Bezug genommen. Diese ist wie folgt definiert: |
| − | |||
| − | * In der Teilaufgabe | ||
:$$\phi(t) = \arctan \hspace{0.15cm} \frac{y(t)}{x(t)} | :$$\phi(t) = \arctan \hspace{0.15cm} \frac{y(t)}{x(t)} | ||
| Zeile 27: | Zeile 24: | ||
| − | + | ''Hinweis:'' | |
| + | * Die Aufgabe gehört zum Kapitel [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings|Wahrscheinlichkeitsdichte des Rayleigh–Fadings]] dieses Buches. | ||
| + | * Eine ähnliche Aufgabenstellung wird im Kapitel [[Stochastische_Signaltheorie/Weitere_Verteilungen|Weitere Verteilungen]] des Buches „Stochastische Signaltheorie” behandelt. | ||
{{Display}} | {{Display}} | ||
Version vom 28. Oktober 2017, 09:48 Uhr
Dargestellt ist der multiplikative Faktor $z(t) = x(t) + j \cdot y(t)$ zweier Mobilfunkkanäle (beide ohne Mehrwegeausbreitung) in 2D–Darstellung. Als gesichert wird vorgegeben:
- Der Kanal R (die Bezeichnung ergibt sich aus der Farbe „Rot” der Punktwolke) ist rayleighverteilt mit $\sigma_{\rm R} = 0.5$.
- Für die Wahrscheinlichkeitsdichtefunktion (WDF) von Betrag $a(t) = |z(t)|$ bzw. Betragsquadrat $p(t) = |z(t)|^2$ gelten somit die folgenden Gleichungen (mit $\sigma = \sigma_{\rm R}$):
- $$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm exp} [ -a^2/(2\sigma^2)] \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm},$$
- $$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm exp} [ -p/(2\sigma^2)] \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} p \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} p < 0 \\ \end{array} .$$
- Vom Kanal B („Blau”) ist nur die Punktwolke gegeben. Es ist abzuschätzen, ob hier ebenfalls Rayleigh–Fading vorliegt, und wenn JA, wie groß bei diesem Kanal die Kenngröße $\sigma = \sigma_{\rm B}$ ist.
- In der Teilaufgabe 3) wird schließlich auch auf die WDF $f_{\it \phi}(\phi)$ der Phasenfunktion $\phi(t)$ Bezug genommen. Diese ist wie folgt definiert:
- $$\phi(t) = \arctan \hspace{0.15cm} \frac{y(t)}{x(t)} \hspace{0.05cm}.$$
Hinweis:
- Die Aufgabe gehört zum Kapitel Wahrscheinlichkeitsdichte des Rayleigh–Fadings dieses Buches.
- Eine ähnliche Aufgabenstellung wird im Kapitel Weitere Verteilungen des Buches „Stochastische Signaltheorie” behandelt.