Aufgaben:Aufgabe 1.3Z: Nochmals Rayleigh–Fading?

• Zurück zum Buch

Zwei Kanäle, jeweils durch den komplexen Faktor z(t) gekennzeichnet

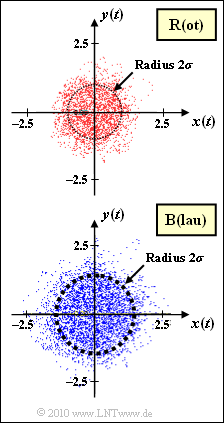
Dargestellt ist der multiplikative Faktor $z(t) = x(t) + {\rm j} \cdot y(t)$ zweier Mobilfunkkanäle (beide ohne Mehrwegeausbreitung) in 2D–Darstellung. Als gesichert wird vorgegeben:

• Der Kanal R (die Bezeichnung ergibt sich aus der Farbe „Rot” der Punktwolke) ist rayleighverteilt mit $\sigma_{\rm R} = 0.5$.
• Für die Wahrscheinlichkeitsdichtefunktion (WDF) von Betrag $a(t) = |z(t)|$ bzw. Betragsquadrat $p(t) = |z(t)|^2$ gelten somit die folgenden Gleichungen (mit $\sigma = \sigma_{\rm R}$):

$$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm},$$

$$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^{ -{p}/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} p \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} p < 0 \\ \end{array} .$$

• Vom Kanal B („Blau”) ist nur die Punktwolke gegeben. Es ist abzuschätzen, ob hier ebenfalls Rayleigh–Fading vorliegt, und wenn JA, wie groß bei diesem Kanal die Kenngröße $\sigma = \sigma_{\rm B}$ ist.
• In der Teilaufgabe (3) wird schließlich auch auf die WDF $f_{\it \phi}(\phi)$ der Phasenfunktion $\phi(t)$ Bezug genommen. Diese ist wie folgt definiert:

$$\phi(t) = \arctan \hspace{0.15cm} \frac{y(t)}{x(t)} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Wahrscheinlichkeitsdichte des Rayleigh–Fadings dieses Buches.
• Eine ähnliche Thematik wird mit anderer Herangehensweise im Kapitel Weitere Verteilungen des Buches „Stochastische Signaltheorie” behandelt.
• Zur Überprüfung Ihrer Ergebnisse können Sie das Interaktionsmodul WDF, VTF und Momente benutzen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Lässt sich auch der Kanal B durch „Rayleigh” modellieren?

	Ja.
	Nein.

2

Schätzen Sie den Rayleigh–Parameter von Kanal B ab. Zur Erinnerung: Bei Kanal R hat dieser Parameter den Wert $\sigma_{\rm R} = 0.5$.

$\sigma_{\rm B}\ = \ $

3

Unterscheiden sich die Phasen–Wahrscheinlichkeitsdichtefunktionen $f_{\it \phi}(\phi)$ von Kanal R und B, und wenn JA, wie?

	Ja.
	Nein.

4

Welchen Verlauf hat in beiden Fällen die WDF $f_a(a)$ mit $a(t) = |z(t)|$?

	Der Betrag $a(t)$ ist gaußverteilt.
	Der Betrag $a(t)$ ist rayleighverteilt.
	Der Betrag $a(t)$ ist positiv–exponentialverteilt.

5

Welchen Verlauf hat in beiden Fällen die WDF $f_p(p)$ mit $p(t) = |z(t)|^2$?

	Der Betrag $p(t)$ ist gaußverteilt.
	Der Betrag $p(t)$ ist rayleighverteilt.
	Der Betrag $p(t)$ ist positiv–exponentialverteilt.

6

Wie groß ist die Wahrscheinlichkeit, dass der Betrag $a(t) = |z(t)|$ größer ist als ein vorgegebener Wert $A$?

	Es gilt ${\rm Pr}(|z(t)|) > A) = {\rm ln}(A/\sigma).$
	Es gilt ${\rm Pr}(|z(t)|) > A) = {\rm e}^{-A^2/2\sigma^2}.$
	Es gilt ${\rm Pr}(|z(t)|) > A) = {\rm e}^{-A/\sigma}.$

7

Berechnen Sie für beide Kanäle die Wahrscheinlichkeit ${\rm Pr}(|z(t)| > 1)$.

Kanal R:$\hspace{0.4cm} {\rm Pr}(|z(t)| > 1)\ = \ $

Kanal B:$\hspace{0.4cm} {\rm Pr}(|z(t)| > 1)\ = \ $

Musterlösung

Musterlösung

(1)  Richtig ist JA. Man erkennt auch hier die Rotationssymmetrie, wenn man berücksichtigt, dass hier nur $N = 10\hspace{0.05cm}000$ Abtastwerte in der komplexen Ebene dargestellt wurden. Außerdem hätten bei NEIN die nachfolgenden Fragen keinen Sinn.

(2)  Durch Vermessen der beiden eingezeichneten Kreise erkennt man, dass beim „blauen” Kanal die Streuungen von Real– und Imaginärteil um etwa den Faktor 1.4 (exakt: $\sqrt{2}$) größer sind als beim „roten” Kanal:

$$\sigma_{\rm B} = \sigma_{\rm R} \cdot \sqrt{2} = 0.5 \cdot \sqrt{2}= {1}/{\sqrt{2}}\hspace{0.15cm} \underline{ \approx 0.707} \hspace{0.05cm}.$$

(3)  Richtig ist NEIN. In beiden Fällen beschreibt $f_{\it \phi}(\phi)$ eine Gleichverteilung zwischen $–\pi$ und $+\pi$. Die größeren Amplituden von Kanal B spielen für die Phasenfunktion $\phi(t)$ keine Rolle.

(4)  Richtig ist der Lösungsvorschlag 2. Bei Rayleigh–Fading sind Realteil $x(t)$ und Imaginärteil $y(t)$ jeweils gaußverteilt. Die Exponentialverteilung ergibt sich für das Betragsquadrat $p(t) = |z(t)|^2$.

(5)  Richtig ist hier der Lösungsvorschlag 3, wie bereits in der Musterlösung zu (4) begründet wurde.

(6)  Der Betrag $a(t)$ ist rayleighverteilt. Somit gilt für die gesuchte Wahrscheinlichkeit.

$${\rm Pr}(a > A) = \int_{A}^{\infty}\frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \hspace{0.15cm}{\rm d}a \hspace{0.05cm}.$$

In einigen Formelsammlungen findet man die Lösung für dieses Integral, aber nicht in allen. Es gilt aber auch mit der einseitig–exponentialverteilten Zufallsgröße $p = a^2$:

$${\rm Pr}(a > A) = {\rm Pr}(p > A^2) = \frac{1}{2\sigma^2} \cdot\int_{A^2}^{\infty} {\rm e}^{ -{p}/(2\sigma^2)} \hspace{0.15cm}{\rm d}p \hspace{0.05cm}.$$

Dieses Integral ist elementar und liefert das Ergebnis:

$${\rm Pr}(a > A) = {\rm e}^{ -{A^2}/(2\sigma^2)} \hspace{0.05cm}.$$

Richtig ist demnach der Lösungsvorschlag 2.

(7)  Für den Kanal R gilt mit $\sigma = 0.5$:

$${\rm Pr}(|z(t)| > 1) = {\rm e}^{-2} \hspace{0.15cm} \underline{ \approx 0.135} \hspace{0.05cm}.$$

In der oberen Grafik auf der Angabenseite entspricht das der Anzahl aller Punkte, die außerhalb des eingezeichneten Kreises liegen, bezogen auf die Anzahl $N = 10.000$ aller Punkte.

Für den Kanal (B) gilt wegen der doppelten Varianz $\sigma^2 = 0.5$ dagegen ${\rm Pr}(|z(t)|>1) = {\rm e}^{\rm –1} \ \underline {\approx \ 0.368}$. Hinweis: Der Bezugskreis hat auch hier den Radius 1. Der im unteren Bild eingezeichnete Kreis hat einen größeren Radius als $A = 1$, nämlich $A = \sqrt{2}\approx 1.414$.