Aufgaben:Aufgabe 2.1: Zweidimensionale Impulsantwort: Unterschied zwischen den Versionen
Aus LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Mobile Kommunikation/Allgemeine Beschreibung zeitvarianter Systeme}} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Mult…“) |
|||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Mobile Kommunikation/Allgemeine Beschreibung zeitvarianter Systeme}} | {{quiz-Header|Buchseite=Mobile Kommunikation/Allgemeine Beschreibung zeitvarianter Systeme}} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID2144__Mob_A_2_1.png|right|frame|Zweidimensionale Impulsantwort]] |
| + | Es soll die zweidimensionale Impulsantwort | ||
| + | :$$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)$$ | ||
| + | |||
| + | gemäß der nebenstehenden Grafik analysiert werden. Die beiden Achsen sind zeitdiskret: | ||
| + | * $\tau$ kennzeichnet die <i>Verzögerungszeit</i> und kann im Beispiel Werte zwischen $0$ und $6 \ \rm \mu s$ annehmen. | ||
| + | * Die <i>absolute Zeit $t$</i> macht Aussagen über die Häufigkeit der Momentaufnahmen und charakterisiert die Zeitvarianz. Es gilt $t = n \cdot T$, wobei $T >> \tau_{\rm max}$ gelten soll. | ||
| + | |||
| + | |||
| + | Die Pfeile in der Grafik markieren verschiedene Diracfunktionen mit den Impulsgewichten $1$ (rot), $1/2$ (blau) und $1/4$ (grün). Das bedeutet, dass hier auch die Verzögerungszeit $\tau$ zeitdiskret ist. | ||
| + | |||
| + | Bei den Messungen der Impulsantworten zu verschiedenen Zeiten $t$ im Sekundenabstand betrug die Auflösung der $\tau$–Achse $2$ Mikrosekunden $(\Delta \tau = 2 \ \rm \mu s)$. Genauer wurden die Echos nicht lokalisiert. | ||
| + | |||
| + | Weiter wird in dieser Aufgabe noch auf folgende Größen Bezug genommen: | ||
| + | * die <i>zeitvariante Übertragungsfunktion</i> entsprechend der Definition | ||
| + | :$$H(f,\hspace{0.05cm} t) | ||
| + | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) | ||
| + | \hspace{0.05cm},$$ | ||
| + | |||
| + | * die Näherung der <i>Kohärenzbandbreite</i> als Kehrwert der maximalen Ausdehnung von $h(\tau, t)$: | ||
| + | :$$B_{\rm K} \hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Themengebiet des Kapitels [[Mobile_Kommunikation/Allgemeine_Beschreibung_zeitvarianter_Systeme| Allgemeine Beschreibung zeitvarianter Systeme]]. | ||
| + | * Genauere Informationen zu verschiedene Definitionen für die Kohärenzbandbreite finden Sie im Kapitel [[Mobile_Kommunikation/Das_GWSSUS%E2%80%93Kanalmodell| Das GWSSUS–Kanalmodell]], insbesondere in der Musterlösung zur Aufgabe [[Aufgabe Z2.7]]. | ||
| + | |||
Version vom 17. November 2017, 19:10 Uhr
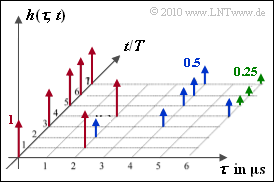
Es soll die zweidimensionale Impulsantwort
- $$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)$$
gemäß der nebenstehenden Grafik analysiert werden. Die beiden Achsen sind zeitdiskret:
- $\tau$ kennzeichnet die Verzögerungszeit und kann im Beispiel Werte zwischen $0$ und $6 \ \rm \mu s$ annehmen.
- Die absolute Zeit $t$ macht Aussagen über die Häufigkeit der Momentaufnahmen und charakterisiert die Zeitvarianz. Es gilt $t = n \cdot T$, wobei $T >> \tau_{\rm max}$ gelten soll.
Die Pfeile in der Grafik markieren verschiedene Diracfunktionen mit den Impulsgewichten $1$ (rot), $1/2$ (blau) und $1/4$ (grün). Das bedeutet, dass hier auch die Verzögerungszeit $\tau$ zeitdiskret ist.
Bei den Messungen der Impulsantworten zu verschiedenen Zeiten $t$ im Sekundenabstand betrug die Auflösung der $\tau$–Achse $2$ Mikrosekunden $(\Delta \tau = 2 \ \rm \mu s)$. Genauer wurden die Echos nicht lokalisiert.
Weiter wird in dieser Aufgabe noch auf folgende Größen Bezug genommen:
- die zeitvariante Übertragungsfunktion entsprechend der Definition
- $$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm},$$
- die Näherung der Kohärenzbandbreite als Kehrwert der maximalen Ausdehnung von $h(\tau, t)$:
- $$B_{\rm K} \hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Themengebiet des Kapitels Allgemeine Beschreibung zeitvarianter Systeme.
- Genauere Informationen zu verschiedene Definitionen für die Kohärenzbandbreite finden Sie im Kapitel Das GWSSUS–Kanalmodell, insbesondere in der Musterlösung zur Aufgabe Aufgabe Z2.7.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)