Aufgaben:Aufgabe 3.2: G–Matrix eines Faltungscodierers

• Zurück zum Buch

Vorgegebener Faltungscoder

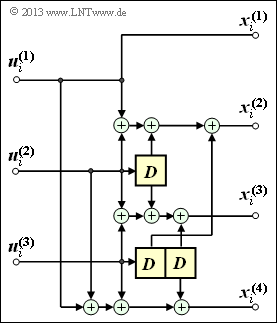
Wir betrachten wie in Aufgabe A3.1 den nebenstehend gezeichneten Faltungscodierer der Rate $3/4$. Dieser wird durch den folgenden Gleichungssatz charakterisiert:

$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$

$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$

$$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-1}^{(2)} + u_{i-2}^{(3)} \hspace{0.05cm},$$

$$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)}\hspace{0.05cm}.$$

Bezieht man sich auf die bei $i = 1$ beginnenden und sich zeitlich bis ins Unendliche erstreckenden Sequenzen

$$\underline{\it u} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left ( \underline{\it u}_1, \underline{\it u}_2, ... \hspace{0.1cm}, \underline{\it u}_i , ... \hspace{0.1cm} \right )\hspace{0.05cm},$$

$$\underline{\it x} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left ( \underline{\it x}_1, \underline{\it x}_2, ... \hspace{0.1cm}, \underline{\it x}_i , ... \hspace{0.1cm} \right )$$

mit $\underline{u}_i = (u_i^{(1)}, u_i^{(2)}, \ ... \ , u_i^{(k)})$ bzw. $\underline{x}_i = (x_i^{(1)}, x_i^{(2)}, \ ... \ , x_i^{(n)})$, so kann der Zusammenhang zwischen der Informationssequenz $\underline{u}$ und der Codesequenz $\underline{x}$ durch die Generatormatrix $\mathbf{G}$ in folgender Form ausgedrückt werden:

$$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$

Für die Generatormatrix eines Faltungscoders mit dem Gedächtnis $m$ ist dabei zu setzen:

$${ \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \ddots & \ddots & & & \ddots \end{pmatrix}\hspace{0.05cm}.$$

Hierbei bezeichnen $\mathbf{G}_0, \mathbf{G}_1, \mathbf{G}_2, \ ...$ Teilmatrizen mit jeweils $k$ Zeilen und $n$ Spalten sowie binären Matrixelementen ($0$ oder $1$). Ist das Matrixelement $\mathbf{G}_l(\kappa, j) = 1$, so bedeutet dies, dass das Codebit $x_i^{(j)}$ durch das Informationsbit $u_{i–l}^{(\kappa)}$ beeinflusst wird. Andernfalls ist dieses Matrixelement gleich $0$.

Ziel dieser Aufgabe ist es, die zur Informationssequenz

$$\underline{u} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm} ,\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm})$$

gehörige Codesequenz $\underline{x}$ entsprechend den obigen Vorgaben zu berechnen. Das Ergebnis müsste mit dem Ergebnis von Aufgabe A3.1 übereinstimmen, das allerdings auf anderem Wege erzielt wurde.

Hinweise:

• Die Aufgabe gehört zum Themengebiet des Kapitels Algebraische und polynomische Beschreibung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Aus wie vielen Teilmatrizen $\mathbf{G}_l$ setzt sich die Matrix $\mathbf{G}$ zusammen?

${\rm Anzahl der Teilmatrizen} \ = \ $

2

Welche Aussagen treffen für die Teilmatrix $\mathbf{G}_0$ zu?

	Insgesamt beinhaltet $\mathbf{G}_0$ acht Einsen.
	Die erste Zeile von $\mathbf{G}_0$ lautet $1 1 0 1$.
	Die erste Zeile von $\mathbf{G}_0$ lautet $1 0 0$.

3

Welche aussagen treffen für die Teilmatrix $\mathbf{G}_1$ zu?

	Die erste Zeile lautet $0 0 0 0$.
	Die zweite Zeile lautet $0 1 1 0$.

4

Ermitteln Sie die ersten neun Zeilen und zwölf Spalten der Generatormatrix $\mathbf{G}$. Welche Aussagen treffen zu?

	Es gibt mindestens eine Zeile mit lauter Nullen.
	Es gibt mindestens eine Zeile mit lauter Einsen.
	In den Spalten $1, 5, 9$ steht jeweils nur eine einzige Eins.

5

Welche Codesequenz $\underline {x}$ ergibt sich für $\underline {u} = (0, 1, 1, 1, 1, 0, 1, 0, 1)$?

	Es gilt: $\underline{x} = (1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, \ ...)$.
	Es gilt: $\underline{x} = (0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, \ ...)$.
	Es gilt: $\underline{x} = (0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, \ ...)$.

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)