Aufgaben:Aufgabe 1.2: Einfacher binärer Kanalcode

• Zurück zum Buch

Zur Verdeutlichung der Kanalcodierung

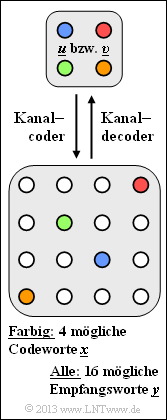
Die Grafik verdeutlicht die hier betrachtete Kanalcodierung C:

• Es gibt vier mögliche Informationsblöcke $\underline{u} = (u_{1}, u_{2}, ... , u_{k})$.
• Jeder Informationsblock u wird eindeutig (erkennbar an der gleichen Farbe) dem Codewort $\underline{x}= (x_{1}, x_{2}, ... , x_{n})$ zugeordnet.
• Aufgrund von Decodierfehlern (0 → 1, 1 → 0) gibt es mehr als 4, nämlich 16 verschiedene Empfangsworte $\underline{y} = (y_{1}, y_{2}, ... , y_{n})$.

Ab Teilaufgabe d) betrachten wir folgende Zuordnung:

$$\underline{u_0} = (0, 0) \leftrightarrow (0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm},$$

$$\underline{u_1} = (0, 1) \leftrightarrow (0, 1, 0, 1) = \underline{x_1}\hspace{0.05cm},$$

$$\underline{u_2} = (1, 0) \leftrightarrow (1, 0, 1, 0) = \underline{x_2}\hspace{0.05cm},$$

$$\underline{u_3} = (1, 1) \leftrightarrow (1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.$$

Hinweis:

Die hier abgefragten Beschreibungsgrößen wie

• Coderate,
• Hamming–Gewicht,
• Hamming–Distanz, usw.

werden auf Blockschaltbild_und_Voraussetzungen und Einige_wichtige_Definitionen_zur_Blockcodierung von Kanalcodierung definiert.

Fragebogen

1

Aus wievielen Binärsymbolen besteht ein Informationsblock?

$k \ = \ $

2

Wie groß ist die Codewortlänge n?

$n \ = \ $

3

Wie groß ist die Coderate?

$R \ = \ $

4

Ist der hier vorgegebene Code systematisch?

	Ja,
	Nein.

5

Geben Sie die Hamming–Gewichte aller Codeworte an.

$ w_{\rm H} \ (\underline{x}_0) \ = \ $

$ w_{\rm H} \ (\underline{x}_1) \ = \ $

$ w_{\rm H} \ (\underline{x}_2) \ = \ $

$ w_{\rm H} \ (\underline{x}_3) \ = \ $

6

Geben Sie die Hamming–Distanzen zwischen folgenden Codeworten an.

$ d_{\rm H} \ (\underline{x}_0, \underline{x}_1) \ = \ $

$ d_{\rm H} \ (\underline{x}_0, \underline{x}_3) \ = \ $

$ d_{\rm H} \ (\underline{x}_1, \underline{x}_2) \ = \ $

7

Wie groß ist die minimale Hamming–Distanz des betrachteten Codes C?

$ d_{\rm min} \ (C) \ = \ $

Musterlösung

Musterlösung

(1)  Der Codeumfang ist hier zu |C| = 4 gegeben. Allgemein gilt |C| = $2^k$. Daraus folgt $\underline{ k = 2}$.

(2)  Jedes Codewort x ist eineindeutig einem Informationsblock u zugeordnet. Durch Verfälschungen einzelner der insgesamt n Bit eines Codewortes x ergeben sich die Empfangsworte y . Aus der Anzahl (16 = $2^4$) der möglichen Empfangsworte folgt $\underline{ n = 4}$.

(3)  Die Coderate ist per Definition R = k/n. Mit den obigen Ergebnissen erhält man R = 1/2.

4. 5. 6. 7.