Aufgaben:Aufgabe 4.12: Berechnungen zur 16-QAM: Unterschied zwischen den Versionen
| Zeile 50: | Zeile 50: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Der Quotient $E_{\rm S}/E$ ergibt sich als der mittlere quadratische Abstand der $M = 16$ Signalraumpunkte $\boldsymbol{s}_i$ vom Ursprung. Mit der gegebenen Signalraumkonstellation der 16–QAM erhält man: | '''(1)''' Der Quotient $E_{\rm S}/E$ ergibt sich als der mittlere quadratische Abstand der $M = 16$ Signalraumpunkte $\boldsymbol{s}_i$ vom Ursprung. Mit der gegebenen Signalraumkonstellation der 16–QAM erhält man: | ||
| − | :$$E_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} { E}/{ 16} \cdot \left [ 4 \cdot (1^2 + 1^2) + 8 \cdot (1^2 + 3^2) + 4 \cdot (3^2 + 3^2)\right ]= | + | :$$E_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} { E}/{ 16} \cdot \left [ 4 \cdot (1^2 + 1^2) + 8 \cdot (1^2 + 3^2) + 4 \cdot (3^2 + 3^2)\right ]={ E}/{ 16} \cdot \left [ 4 \cdot 2 + 8 \cdot 10 + 4 \cdot 18\right ] = 10 \cdot E = \underline{10 \ {\rm mWs}} |
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 57: | Zeile 56: | ||
:$$E_{\rm S} = \frac{ 2 \cdot (M-1)}{ 3 } \cdot E = \frac{ 2 \cdot 15}{ 3 } \cdot E = 10 E | :$$E_{\rm S} = \frac{ 2 \cdot (M-1)}{ 3 } \cdot E = \frac{ 2 \cdot 15}{ 3 } \cdot E = 10 E | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
'''(2)''' Jedes einzelne Symbol stellt vier Binärsymbole dar. Damit ist die mittlere Energie pro Bit. | '''(2)''' Jedes einzelne Symbol stellt vier Binärsymbole dar. Damit ist die mittlere Energie pro Bit. | ||
| − | :$$E_{\rm B} = \frac{ E_{\rm S}}{ {\rm log_2} \hspace{0.05cm}(M)} = 2.5 \cdot E = \underline{2.5 \ | + | :$$E_{\rm B} = \frac{ E_{\rm S}}{ {\rm log_2} \hspace{0.05cm}(M)} = 2.5 \cdot E = \underline{2.5 \ {\rm mWs}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | [[Datei:P_ID2063__Dig_A_4_12c.png|right|frame|Zur Verdeutlichung der 16–QAM–Fehlerwahrscheinlichkeit]] | |
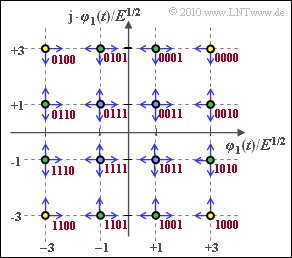
| − | + | '''(3)''' Die <i>Union Bound</i> ist eine obere Schranke für die Symbolfehlerwahrscheinlichkeit. Sie berücksichtigt nur den Übergang zu benachbarten Entscheidungsregionen aufgrund von AWGN–Rauschen. | |
Aus der Grafik geht hervor, dass die Ecksymbole (gelb gefüllt) nur zu zwei anderen Symbolen hin verfälscht werden können und die restlichen Randsymbole (grüne Füllung) in drei Richtungen. Der „worst case” sind die vier inneren Symbole (mit blauer Füllung) mit jeweils vier Verfälschungsmöglichkeiten. Daraus folgt: | Aus der Grafik geht hervor, dass die Ecksymbole (gelb gefüllt) nur zu zwei anderen Symbolen hin verfälscht werden können und die restlichen Randsymbole (grüne Füllung) in drei Richtungen. Der „worst case” sind die vier inneren Symbole (mit blauer Füllung) mit jeweils vier Verfälschungsmöglichkeiten. Daraus folgt: | ||
| − | :$$p_{\rm S} = {\rm Pr}({\cal{E}}) \le 4 \cdot p = \underline{ | + | :$$p_{\rm S} = {\rm Pr}({\cal{E}}) \le 4 \cdot p = \underline{1.6\%}= p_{\rm UB} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
'''(4)''' Zählt man die blauen Pfeile in obiger Grafik, so kommt man auf $4 \cdot 2 + 8 \cdot 3 + 4 \cdot 4 = 48$. Die mittlere Symbolfehlerwahrscheinlichkeit ist somit gleich | '''(4)''' Zählt man die blauen Pfeile in obiger Grafik, so kommt man auf $4 \cdot 2 + 8 \cdot 3 + 4 \cdot 4 = 48$. Die mittlere Symbolfehlerwahrscheinlichkeit ist somit gleich | ||
| − | :$$p_{\rm S} = { E}/{ 16} \cdot 48 p = 3p = \underline{ | + | :$$p_{\rm S} = { E}/{ 16} \cdot 48 p = 3p = \underline{1.2\%} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 80: | Zeile 78: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Beide Gleichungen gelten nur dann exakt, wenn man wie hier diagonale Verfälschungen ausschließt. | |
'''(5)''' Bei Graycodierung entsprechend der roten Beschriftung in der Grafik bewirkt jeder Symbolfehler genau einen Bitfehler. Da aber mit jedem Symbol $M = 4$ Binärsymbole übertragen werden, ist | '''(5)''' Bei Graycodierung entsprechend der roten Beschriftung in der Grafik bewirkt jeder Symbolfehler genau einen Bitfehler. Da aber mit jedem Symbol $M = 4$ Binärsymbole übertragen werden, ist | ||
:$$p_{\rm B} = \frac{ p_{\rm S}}{ {\rm log_2} \hspace{0.05cm}(M)} | :$$p_{\rm B} = \frac{ p_{\rm S}}{ {\rm log_2} \hspace{0.05cm}(M)} | ||
| − | = \frac{ | + | = \frac{ 1.2\%}{ 4} = \underline{0.3\%} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 23. November 2017, 16:31 Uhr
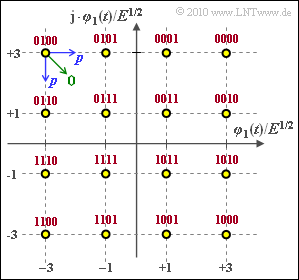
Beigefügte Grafik zeigt die Signalraumkonstellation der Quadraturamplitudenmodulation mit $M = 16$ Signalraumpunkten. Für dieses Modulationsverfahren sollen berechnet werden:
- die mittlere Energie pro Symbol bzw. pro Bit,
- die mittlere Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ sowie die Union Bound als obere Schranke,
- die mittlere Bitfehlerwahrscheinlichkeit $p_{\rm B}$ bei Graycodierung. Die Gray–Zuordnung ist in der Grafik angegeben (rote Beschriftung).
Hinweise:
- Die Aufgabe behandelt einen Teilaspekt des Kapitels Trägerfrequenzsysteme mit kohärenter Demodulation.
- Die Wahrscheinlichkeit, dass das linke obere Symbol in eines der benachbarten Symbole verfälscht wird, wird mit $p$ abgekürzt (blaue Pfeile in der Grafik).
- Eine diagonale Verfälschung ⇒ zwei Bit verfälscht (grüner Pfeil) wird ausgeschlossen.
- Für den AWGN–Kanal gilt mit dem komplementären Gaußschen Fehlerintegrale für diese Hilfsgröße: $p = {\rm Q} \left ( \sqrt{ { 2E}/{ N_0} }\right )\hspace{0.05cm}.$
- Verwenden Sie für numerische Berechnungen $E = 1 \ \rm mWs$ und $p = 0.4\%$. Aus diesen Werten kann die AWGN–Rauschleistungsdichte $N_0$ näherungsweise berechnet werden:
- $$p = {\rm Q} \left ( \sqrt{ { 2E}/{ N_0} }\right ) = 0.004 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} { 2E}{ N_0} \approx 2.65^2 \approx 7 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} N_0 = { E}/{ 3.5}\approx 1.4 \cdot 10^{-4}\,{\rm W/Hz} \hspace{0.05cm}.$$
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$E_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} { E}/{ 16} \cdot \left [ 4 \cdot (1^2 + 1^2) + 8 \cdot (1^2 + 3^2) + 4 \cdot (3^2 + 3^2)\right ]={ E}/{ 16} \cdot \left [ 4 \cdot 2 + 8 \cdot 10 + 4 \cdot 18\right ] = 10 \cdot E = \underline{10 \ {\rm mWs}} \hspace{0.05cm}.$$
Zum gleichen Ergebnis kommt man mit der im Theorieteil angegebenen Gleichung
- $$E_{\rm S} = \frac{ 2 \cdot (M-1)}{ 3 } \cdot E = \frac{ 2 \cdot 15}{ 3 } \cdot E = 10 E \hspace{0.05cm}.$$
(2) Jedes einzelne Symbol stellt vier Binärsymbole dar. Damit ist die mittlere Energie pro Bit.
- $$E_{\rm B} = \frac{ E_{\rm S}}{ {\rm log_2} \hspace{0.05cm}(M)} = 2.5 \cdot E = \underline{2.5 \ {\rm mWs}} \hspace{0.05cm}.$$
(3) Die Union Bound ist eine obere Schranke für die Symbolfehlerwahrscheinlichkeit. Sie berücksichtigt nur den Übergang zu benachbarten Entscheidungsregionen aufgrund von AWGN–Rauschen.
Aus der Grafik geht hervor, dass die Ecksymbole (gelb gefüllt) nur zu zwei anderen Symbolen hin verfälscht werden können und die restlichen Randsymbole (grüne Füllung) in drei Richtungen. Der „worst case” sind die vier inneren Symbole (mit blauer Füllung) mit jeweils vier Verfälschungsmöglichkeiten. Daraus folgt:
- $$p_{\rm S} = {\rm Pr}({\cal{E}}) \le 4 \cdot p = \underline{1.6\%}= p_{\rm UB} \hspace{0.05cm}.$$
(4) Zählt man die blauen Pfeile in obiger Grafik, so kommt man auf $4 \cdot 2 + 8 \cdot 3 + 4 \cdot 4 = 48$. Die mittlere Symbolfehlerwahrscheinlichkeit ist somit gleich
- $$p_{\rm S} = { E}/{ 16} \cdot 48 p = 3p = \underline{1.2\%} \hspace{0.05cm}.$$
Zum gleichen Ergebnis kommt man mit der im Theorieteil angegebenen Gleichung
- $$p_{\rm S} = 4p \cdot \left [ 1 - { 1}/{ \sqrt{M}} \right ] = 4p \cdot \left [ 1 - { 1}/{ 4} \right ] = 3p \hspace{0.05cm}.$$
Beide Gleichungen gelten nur dann exakt, wenn man wie hier diagonale Verfälschungen ausschließt.
(5) Bei Graycodierung entsprechend der roten Beschriftung in der Grafik bewirkt jeder Symbolfehler genau einen Bitfehler. Da aber mit jedem Symbol $M = 4$ Binärsymbole übertragen werden, ist
- $$p_{\rm B} = \frac{ p_{\rm S}}{ {\rm log_2} \hspace{0.05cm}(M)} = \frac{ 1.2\%}{ 4} = \underline{0.3\%} \hspace{0.05cm}.$$