Aufgaben:Aufgabe 1.4Z: Modifizierter MS43–Code

• Zurück zum Buch

Codetabelle des MMS43-Codes

Bei der ISDN–Datenübertragung wird in Deutschland und Belgien auf der so genannten $U_{\rm K0}$–Schnittstelle (Übertragungsstrecke zwischen der Vermittlungsstelle und dem NTBA) der MMS43–Code eingesetzt. Die Abkürzung „MMS43” steht für Modified Monitored Sum 4B3T.

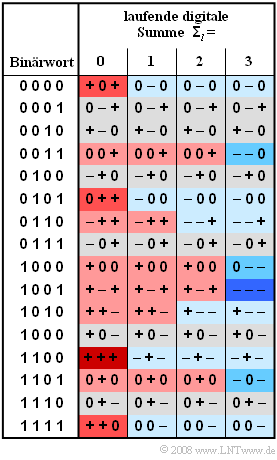
Es handelt sich hierbei um einen 4B3T–Blockcode mit den vier in der Grafik gezeigten Codetabellen, die gemäß der sog. „Laufenden Digitalen Summe” (nach $l$–Blöcken)

$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.05cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu$$

zur Codierung benutzt werden. Zur Initialisierung wird $\Sigma_{0} = 0$ verwendet. Die Farbgebungen in der Grafik bedeuten:

• Ändert sich die laufende digitale Summe nicht (gilt also $\Sigma_{l+1} = \Sigma _{l}$), so ist ein Feld hellgrau hinterlegt.
• Eine Zunahme ($\Sigma_{l+1} > \Sigma_{l}$) ist rot hinterlegt, eine Abnahme ($\Sigma_{l+1} < \Sigma _{l}$) blau.
• Je intensiver diese Farben sind, um so größer ist die Änderung der laufenden digitalen Summe.

Hinweis:

Diese Aufgabe bezieht sich auf ISDN-Basisanschluss dieses Buches sowie auf Blockweise Codierung mit 4B3T-Codes des Buches „Digitalsignalübertragung”.

Fragebogen

1

Was sind Gründe dafür, dass bei ISDN statt des redundanzfreien Binärcodes ein 4B3T–Code verwendet wird?

	4B3T ist prinzipiell besser als der redundanzfreie Binärcode.
	Bei $H_{\rm K}(f = 0) = 0$ sollte das Sendesignal gleichsignalfrei sein.
	Eine kleine Symbolrate ($1/T$) ermöglicht größere Kabellänge.

2

Codieren Sie die Binärfolge „1100 0100 0110 1010” gemäß der Tabelle. Wie lautet der Koeffizient des dritten Ternärsymbols des vierten Blocks?

$a_{12} \ = \ $

3

Ermitteln Sie das Markovdiagramm für den Übergang von $\Sigma_{l}$ auf $\Sigma_{l+1}$. Welche Übergangswahrscheinlichkeiten ergeben sich?

${\rm Pr}(\Sigma_{l+1} = 0 \ | \ \Sigma_{l}=0) \ = \ $

${\rm Pr}(\Sigma_{l+1} = 2 \ | \ \Sigma_{l}=0) \ = \ $

${\rm Pr}(\Sigma_{l+1} = 0 \ | \ \Sigma_{l}=2) \ = \ $

4

Welche Eigenschaften folgen aus dem Markovdiagramm?

	Die Wahrscheinlichkeiten ${\rm Pr}(\Sigma_{l} = 0), ... , {\rm Pr}(\Sigma_{l} = 3)$ sind gleich.
	Es gilt ${\rm Pr}(\Sigma_{l} = 0) = {\rm Pr}(\Sigma_{l} = 3)$ und ${\rm Pr}(\Sigma_{l} = 1) = {\rm Pr}(\Sigma_{l} = 2)$.
	Die Extremwerte (0 bzw. 3) treten seltener auf als 1 oder 2.

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)  (6)  (7)