Aufgaben:Aufgabe 1.16: Fehlerwahrscheinlichkeitsschranken für AWGN

• Zurück zum Buch

Funktion Q(x) und Näherungen

Wir gehen von der folgenden Konstellation aus:

• ein linearer Blockcode mit der Coderate $R = k/n$ und dem Distanzspektrum { $W_{i}$ }, $i = 1, ... , n,$

• ein AWGN–Kanal, gekennzeichnet durch „$E_{\rm B}/N_{0}$” ⇒ umrechenbar in die Rauschleistung $\sigma^2$,

• ein Empfänger, basierend auf Soft Decision sowie dem Maximum–Likelihood–Kriterium.

Unter der für die gesamte Aufgabe gültigen Annahme, dass stets das Nullwort $\underline{x}_{1} = (0, 0, ... , 0)$ gesendet wird, gilt für die „paarweise Fehlerwahrscheinlichkeit” mit einem anderen Codewort $\underline{x}_{l} (l = 2, ... , 2^k):$

$$ {\rm Pr}[\hspace{0.05cm}\underline{x}_{\hspace{0.02cm}1} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}l}\hspace{0.05cm}] = {\rm Q}\left ( \sqrt{w_{\rm H}(\underline{x}_{\hspace{0.02cm}l})/\sigma^2} \right ) \hspace{0.05cm}.$$

Die Herleitung dieser Beziehung finden Sie in [Liv10]. In dieser Gleichung wurden verwendet:

• die komplementäre Gaußsche Fehlerfunktion ${\rm Q}(x)$,

• das Hamming–Gewicht $w_{\rm H}(\underline{x}_{l})$ des Codewortes $\underline{x}_{l}$,

• die AWGN–Rauschleistung $\sigma^2 = (2 · R · E_{\rm B}/N_{0})^{–1}.$

Damit lassen sich verschiedene Schranken für die Blockfehlerwahrscheinlichkeit angeben:

• die sogenannte Union Bound:

$$p_1 = \sum_{l = 2}^{2^k}\hspace{0.05cm}{\rm Pr}[\hspace{0.05cm}\underline{x}_{\hspace{0.02cm}1} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}l}\hspace{0.05cm}] = \sum_{l = 2}^{2^k}\hspace{0.05cm}{\rm Q}\left ( \sqrt{w_{\rm H}(\underline{x}_{\hspace{0.02cm}l})/\sigma^2} \right ) \hspace{0.05cm},$$

• die so genannte Truncated Union Bound (TUB):

$$p_2 = W_{d_{\rm min}} \cdot {\rm Q}\left ( \sqrt{d_{\rm min}/\sigma^2} \right ) \hspace{0.05cm},$$

• die Bhattacharyya–Schranke:

$$p_3 = W(\beta) - 1\hspace{0.05cm},\hspace{0.2cm} {\rm mit}\hspace{0.15cm} \beta = {\rm exp}\left [ - 1/(2\sigma^2) \right ] \hspace{0.05cm}.$$

In diesem Fall ist das Distanzspektrum { $W_{i}$ } durch die Gewichtsfunktion zu ersetzen:

$$\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} W(X) = \sum_{i=0 }^{n} W_i \cdot X^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.$$

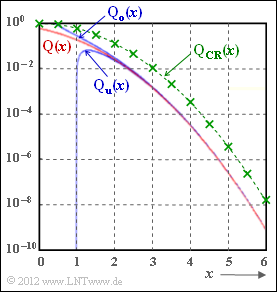
Beim Übergang von der Union Bound $p_{1}$ zur Schranke $p_{3}$ wird unter Anderem die Funktion ${\rm Q}(x)$ durch die Chernoff–Rubin–Schranke ${\rm Q}_{\rm CR}(x)$ ersetzt. Beide Funktionen sind in obigerer Grafik dargestellt (rote bzw. grüne Kurve).

In der Aufgabe 1.16Z wird der Zusammenhang zwischen diesen Funktionen numerisch ausgewertet und Bezug genommen zu den Schranken ${\rm Q}_{o}(x)$ und ${\rm Q}_{u}(x)$, die in obiger Grafik ebenfalls eingezeichnet sind.

Hinweis:

Die Aufgabe gehört zum Kapitel Schranken für die Blockfehlerwahrscheinlichkeit Weiter verweisen wir auf folgendes Flash–Modul:

Komplimentäre Gaußsche Fehlerfunktion (Dateigröße: 235 kB)

Fragebogen

1

Welche Gleichung gilt für die Union Bound?

	$p_{1} = {\rm Summe}$ (über $l = 2, ... , 2^k$) $W_{l} · {\rm Q}[(l/\sigma^2)^{0.5}],$
	$p_{1} = {\rm Summe}$ (über $i = 1, ... , n$) $W_{i} · {\rm Q}[(i/\sigma^2)^{0.5}],$

2

Geben Sie die Union Bound für den (8, 4, 4)–Code und $\sigma = 1$, $\sigma = 0.5$ an.

$\ (8, 4, 4)–Code, \sigma = 1: p_{1}$ =

$\ \sigma = 0.5: \ \ \ p_{1}$ = $\ \cdot 10^{-3} $

3

Was liefert die Truncated Union Bound bei gleichen Randbedingungen?

$\ (8, 4, 4)–Code, \sigma = 1: p_{2}$ =

$\ \sigma = 0.5: \ \ \ p_{2}$ = $\ \cdot 10^{-3} $

4

Welche Aussage gilt immer (für alle Konstellationen)?

	Die Blockfehlerwahrscheinlichkeit ist nie größer als $p_{1}$.
	Die Blockfehlerwahrscheinlichkeit ist nie größer als $p_{2}$.

5

Wie kommt man von $p_{1}$ zur Bhattacharyya–Schranke $p_{3}$? Dadurch, dass man

	die Fehlerfunktion ${\rm Q}(x)$ durch die Funktion ${\rm Q}_{\rm CR}(x)$ ersetzt,
	den Bhattacharyya–Parameter $\beta = 1/\sigma$ setzt,
	statt { $W_{i}$ } die Gewichtsfunktion $W(X)$ verwendet.

6

Geben Sie die Bhattacharyya–Schranke für $\sigma = 1$ und $\sigma = 0.5$ an.

$\ (8, 4, 4)–Code, \sigma = 1: p_{3}$ =

$\ \sigma = 0.5: \ \ \ p_{3}$ = $\ \cdot 10^{-2} $

Musterlösung

Musterlösung

(1)  Richtig ist Antwort 2. Das Distanzspektrum { $W_{i}$ } ist definiert für $i = 0, ... , n$:

• $W_{1}$ gibt an, wie oft das Hamming–Gewicht $w_{\rm H}(\underline{x}_{i}) = 1$ auftritt.
• $W_{n}$ gibt an, wie oft das Hamming–Gewicht $w_{\rm H}(\underline{x}_{i}) = n$ auftritt.

Damit lautet die Union Bound:

$$p_1 = {\rm Pr(Union \hspace{0.15cm}Bound)}= \sum_{i = 1}^{n}\hspace{0.05cm}W_i \cdot {\rm Q}\left ( \sqrt{i/\sigma^2} \right ) \hspace{0.05cm}.$$

(2)  Das Distanzspektrum des (8, 4, 4)–Codes wurde mit $W_{0} = 1 , W_{4} = 14, W_{8} = 1$ angegeben. Somit erhält man für $\boldsymbol{\sigma = 1}$:

bzw. für $\boldsymbol{\sigma = 0.5}$:

(3)  Mit der Minimaldistanz $d_{\rm min} = 4$ erhält man:

$$\sigma = 1.0: \hspace{0.2cm} p_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} W_4 \cdot {\rm Q}\left ( 2 \right ) \hspace{0.15cm}\underline{= 0.3192}\hspace{0.05cm},$$

$$\sigma = 0.5: \hspace{0.2cm} p_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm}W_4 \cdot {\rm Q}\left ( 4 \right ) \approx p_1 \hspace{0.15cm}\underline{ = 0.444 \cdot 10^{-3}}\hspace{0.05cm}.$$

(4)  Richtig ist Antwort 1. Die Union Bound – hier mit $p_{1}$ bezeichnet – ist in jedem Fall eine obere Schranke für die Blockfehlerwahrscheinlichkeit. Für die Schranke $p_{2}$ (Truncated Union Bound) trifft das nicht immer zu. Beispielsweise erhält man beim (7, 4, 3)–Hamming–Code ⇒ $W_{3} = W_{4} = 7, W_{7} = 1$ und der Streuung $\sigma = 1:$

$$p_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 7 \cdot {\rm Q}\left ( \sqrt{3} \right ) = 7 \cdot 4.18 \cdot 10^{-2} \approx 0.293\hspace{0.05cm},$$

$$p_1 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} p_2 + 7 \cdot {\rm Q}\left ( \sqrt{4} \right )+ 1 \cdot {\rm Q}\left ( \sqrt{7} \right ) \approx 0.455 \hspace{0.05cm}.$$

Die tatsächliche Blockfehlerwahrscheinlichkeit wird wahrscheinlich zwischen $p_{2} = 0.293$ und $p_{1} = 0.455$ liegen (wurde nicht nachgeprüft). Das heißt: $p_{2}$ ist keine obere Schranke.

(5)  Richtig sind die Lösungsvorschläge 1 und 3, wie die folgende Rechnung für den (8, 4, 4)–Code zeigt:

• Es gilt Q(x) ≤ QCR(x) = exp(– x2/2). Damit kann für die Union Bound

$$p_1 = W_4 \cdot {\rm Q}\left ( \sqrt{4/\sigma^2} \right ) +W_8 \cdot {\rm Q}\left ( \sqrt{8/\sigma^2} \right )$$

eine weitere obere Schranke angegeben werden:

$$p_1 \le W_4 \cdot {\rm exp}\left [ - {4}/(2 \sigma^2) \right ] +W_8 \cdot {\rm exp}\left [ - {8}/(2 \sigma^2) \right ] \hspace{0.05cm}.$$

• Mit $\beta = {\rm exp}[–1/(2\sigama^2)]$ kann hierfür auch geschrieben werden (das vorgegebene $\beta = 1/\sigma$ ist also falsch):

$$p_1 \le W_4 \cdot \beta^4 + W_8 \cdot \beta^8 \hspace{0.05cm}.$$

• Die Gewichtsfunktion des (8, 4, 4)–Codes lautet:

$$W(X) = 1 + W_4 \cdot X^4 + W_8 \cdot X^8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W(\beta) - 1 = W_4 \cdot \beta^4 + W_8 \cdot \beta^8$$

$$\Rightarrow \hspace{0.3cm} p_3 = W(\beta) - 1 \ge p_1\hspace{0.05cm}.$$

(6)  Mit σ = 1 lautet der Bhattacharyya–Parameter β = exp(–0.5) = 0.6065 und man erhält damit für die Bhattacharyya–Schranke:

Berücksichtigt man, dass p3 (eine Schranke für) eine Wahrscheinlichkeit angibt, so ist p3 = 1.913 nur eine triviale Schranke. Für σ = 0.5 ergibt sich dagegen β = exp(–2) ≈ 0.135. Dann gilt:

Ein Vergleich mit der Teilaufgabe b) zeigt, dass im vorliegenden Beispiel die Bhattacharyya–Schranke p3 um den Faktor (4.7 · 10–3)/(0.44 · 10–3) > 10 oberhalb der Union Bound p1 liegt. Der Grund für diese große Abweichung ist die Chernoff–Rubin–Schranke, die deutlich oberhalb der Q–Funktion liegt. In der Aufgabe Z1.16 wird die Abweichung zwischen QCR und Q(x) auch quantitativ berechnet: