Aufgaben:Aufgabe 2.5Z: Rechtecksignale: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 2.5Z Rechtecksignale nach Aufgabe 2.5Z: Rechtecksignale) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID323__Sig_Z_2_5.png|right| | + | [[Datei:P_ID323__Sig_Z_2_5.png|right|frame|Verschiedene Rechtecksignale]] |
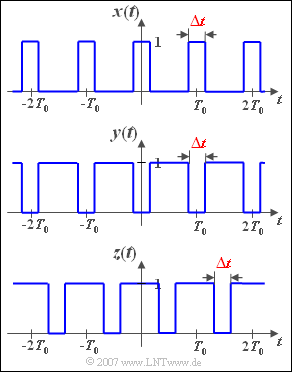
Das mit der Zeit $T_0$ periodische Signal $x(t)$ wird durch den einzigen Parameter $\Delta t$ beschrieben; die Amplitude der Rechteckimpulse sei jeweils $1$. Da $x(t)$ gerade ist, sind alle Sinuskoeffizienten $B_n = 0$. | Das mit der Zeit $T_0$ periodische Signal $x(t)$ wird durch den einzigen Parameter $\Delta t$ beschrieben; die Amplitude der Rechteckimpulse sei jeweils $1$. Da $x(t)$ gerade ist, sind alle Sinuskoeffizienten $B_n = 0$. | ||
Der Gleichsignalkoeffizient ist $A_0 = \Delta t/T_0$ und für die Cosinuskoeffizienten gilt: | Der Gleichsignalkoeffizient ist $A_0 = \Delta t/T_0$ und für die Cosinuskoeffizienten gilt: | ||
:$$A_n=\frac{2}{n\pi}\cdot \sin(n\pi \Delta t/T_0).$$ | :$$A_n=\frac{2}{n\pi}\cdot \sin(n\pi \Delta t/T_0).$$ | ||
| − | In den Teilaufgaben 1) und 2) wird das Signal $x(t)$ für die zwei Parameterwerte $\Delta t/T_0 = 0.5$ bzw. $\Delta t/T_0 = 0.25$ analysiert. Danach betrachten wir die beiden ebenfalls in der Abbildung dargestellten Signale $y(t)$ und $z(t)$, jeweils mit $\Delta t/T_0 = 0.25$. | + | In den Teilaufgaben (1) und (2) wird das Signal $x(t)$ für die zwei Parameterwerte $\Delta t/T_0 = 0.5$ bzw. $\Delta t/T_0 = 0.25$ analysiert. Danach betrachten wir die beiden ebenfalls in der Abbildung dargestellten Signale $y(t)$ und $z(t)$, jeweils mit $\Delta t/T_0 = 0.25$. |
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fourierreihe|Fourierreihe]]. | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fourierreihe|Fourierreihe]]. | ||
| − | *Eine kompakte Zusammenfassung der Thematik finden Sie in den | + | *Eine kompakte Zusammenfassung der Thematik finden Sie in den beiden Lernvideos |
| + | :[[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|Zur Berechnung der Fourierkoeffizienten]] sowie [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]]. | ||
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
| + | |||
| Zeile 38: | Zeile 44: | ||
{Wie groß ist der Gleichanteil des Signals ${y(t)}$? | {Wie groß ist der Gleichanteil des Signals ${y(t)}$? | ||
|type="{}"} | |type="{}"} | ||
| − | + | $A_0 \ = \ $ { 0.75 3% } | |
{Welcher Zusammenhang besteht zwischen den Signalen $x(t)$ und ${y(t)}$? Geben Sie mit Hilfe dieser Überlegungen die Fourierkoeffizienten von ${y(t)}$ an. Wie groß sind die Koeffizienten $A_1$ und $A_2$ dieses Signals? | {Welcher Zusammenhang besteht zwischen den Signalen $x(t)$ und ${y(t)}$? Geben Sie mit Hilfe dieser Überlegungen die Fourierkoeffizienten von ${y(t)}$ an. Wie groß sind die Koeffizienten $A_1$ und $A_2$ dieses Signals? | ||
|type="{}"} | |type="{}"} | ||
| − | + | $A_1\ = \ $ { -0.46--0.44 } | |
| − | $A_2 = $ { -0.325--0.315 } | + | $A_2 \ = \ $ { -0.325--0.315 } |
{Welcher Zusammenhang besteht zwischen den Signalen ${y(t)}$ und ${z(t)}$? Wie groß sind die Koeffizienten $A_1$ und $A_2$ des Signals ${z(t)}$? Überprüfen Sie das Ergebnis anhand der angebenen Koeffizienten des Signals $x(t)$. | {Welcher Zusammenhang besteht zwischen den Signalen ${y(t)}$ und ${z(t)}$? Wie groß sind die Koeffizienten $A_1$ und $A_2$ des Signals ${z(t)}$? Überprüfen Sie das Ergebnis anhand der angebenen Koeffizienten des Signals $x(t)$. | ||
|type="{}"} | |type="{}"} | ||
| − | + | $A_1 \ = \ $ { 0.45 3% } | |
| − | $A_2 =$ { -0.325--0.315 } | + | $A_2 \ = \ $ { -0.325--0.315 } |
| Zeile 58: | Zeile 64: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)'' Richtig sind die <u>Aussagen 1, 3 und 5</u>.: |
*Die Spektralfunktion beinhaltet eine Diracfunktion bei $f = 0$ mit dem Gewicht $0.5$ (Gleichanteil) sowie weitere Spektrallinien bei ungeradzahligen Vielfachen ($n = \pm1, \pm3, \pm5,...$) von $f_0$. | *Die Spektralfunktion beinhaltet eine Diracfunktion bei $f = 0$ mit dem Gewicht $0.5$ (Gleichanteil) sowie weitere Spektrallinien bei ungeradzahligen Vielfachen ($n = \pm1, \pm3, \pm5,...$) von $f_0$. | ||
*Die Gewichte bei $\pm f_0$ sind jeweils $A_1/2 = 1/\pi = 0.318$. | *Die Gewichte bei $\pm f_0$ sind jeweils $A_1/2 = 1/\pi = 0.318$. | ||
| − | '''2 | + | '''(2)'' Richtig sind die <u>Aussagen 1, 2 und 4</u>: |
*Bei allen ungeradzahligen Vielfachen der Grundfrequenz existieren Spektrallinien, zusätzlich noch bei den $2–{\rm fachen}$, $6–{\rm fachen}$ und $10–{\rm fachen}$. | *Bei allen ungeradzahligen Vielfachen der Grundfrequenz existieren Spektrallinien, zusätzlich noch bei den $2–{\rm fachen}$, $6–{\rm fachen}$ und $10–{\rm fachen}$. | ||
*Beispielsweise gilt $A_1 = 1/\pi = 0.450$. ????? Die Spektrallinie bei $2f_0$ hat somit das Gewicht $A_2/2 = 1/(2\pi) = 0.159$. | *Beispielsweise gilt $A_1 = 1/\pi = 0.450$. ????? Die Spektrallinie bei $2f_0$ hat somit das Gewicht $A_2/2 = 1/(2\pi) = 0.159$. | ||
| Zeile 68: | Zeile 74: | ||
*Für $n = 4$, $n = 8$, usw. sind dagegen die Koeffizienten $A_n = 0$, da für die Sinusfunktion gilt: $\sin(\pi) = \sin(2\pi) = ... = 0$. | *Für $n = 4$, $n = 8$, usw. sind dagegen die Koeffizienten $A_n = 0$, da für die Sinusfunktion gilt: $\sin(\pi) = \sin(2\pi) = ... = 0$. | ||
| − | '''3 | + | '''(3)'' Aus der grafischen Darstellung des Signals ${y(t)}$ wird deutlich, dass $A_0 = 0.75$ gelten muss. Zum gleichen Ergebnis kommt man über die Beziehung: |
:$$A_0^{(y)}=1-A_0^{(x)}=1-0.25\hspace{0.15cm}\underline{=0.75}.$$ | :$$A_0^{(y)}=1-A_0^{(x)}=1-0.25\hspace{0.15cm}\underline{=0.75}.$$ | ||
| − | '''4 | + | '''(4)'' Es gilt ${y(t)} = 1 – x(t)$. Für $n \neq 0$ ergeben sich somit die gleichen Fourierkoeffizienten wie für das Signal $x(t)$, jedoch mit negativen Vorzeichen. Inbesondere gilt: |
:$$A_1^{(y)} = -A_1^{(x)}=-{2}/{\pi} \cdot \sin({\pi}/{4})= -{\sqrt2}/{\pi}\hspace{0.15cm}\underline{\approx -0.450},$$ | :$$A_1^{(y)} = -A_1^{(x)}=-{2}/{\pi} \cdot \sin({\pi}/{4})= -{\sqrt2}/{\pi}\hspace{0.15cm}\underline{\approx -0.450},$$ | ||
:$$A_2^{(y)} = -A_2^{(x)}=-{1}/{\pi}\hspace{0.15cm}\underline{ \approx - 0.318}.$$ | :$$A_2^{(y)} = -A_2^{(x)}=-{1}/{\pi}\hspace{0.15cm}\underline{ \approx - 0.318}.$$ | ||
| − | '''5 | + | '''(5)'' Es gilt ${z(t)} = y(t – T_0/2)$. Mit der Fourierreihendarstellung von ${y(t)}$ folgt daraus: |
:$$z(t)=A_0+A_1^{(y)}\cos(\omega_0(t-\frac{T_0}{2}))+A_2^{(y)}\cos(2\omega_0(t-\frac{T_0}{2}))+A_3^{(y)}\cos(3\omega_0(t-\frac{T_0}{2}))+\ldots$$ | :$$z(t)=A_0+A_1^{(y)}\cos(\omega_0(t-\frac{T_0}{2}))+A_2^{(y)}\cos(2\omega_0(t-\frac{T_0}{2}))+A_3^{(y)}\cos(3\omega_0(t-\frac{T_0}{2}))+\ldots$$ | ||
:$$\Rightarrow \quad z(t)=A_0-A_1^{(y)}\cos(\omega_0 t)+A_2^{(y)}\cos(2\omega_0 t)-A_3^{(y)}\cos(3\omega_0 t)+\ldots$$ | :$$\Rightarrow \quad z(t)=A_0-A_1^{(y)}\cos(\omega_0 t)+A_2^{(y)}\cos(2\omega_0 t)-A_3^{(y)}\cos(3\omega_0 t)+\ldots$$ | ||
Version vom 20. Dezember 2017, 13:43 Uhr
Das mit der Zeit $T_0$ periodische Signal $x(t)$ wird durch den einzigen Parameter $\Delta t$ beschrieben; die Amplitude der Rechteckimpulse sei jeweils $1$. Da $x(t)$ gerade ist, sind alle Sinuskoeffizienten $B_n = 0$.
Der Gleichsignalkoeffizient ist $A_0 = \Delta t/T_0$ und für die Cosinuskoeffizienten gilt:
- $$A_n=\frac{2}{n\pi}\cdot \sin(n\pi \Delta t/T_0).$$
In den Teilaufgaben (1) und (2) wird das Signal $x(t)$ für die zwei Parameterwerte $\Delta t/T_0 = 0.5$ bzw. $\Delta t/T_0 = 0.25$ analysiert. Danach betrachten wir die beiden ebenfalls in der Abbildung dargestellten Signale $y(t)$ und $z(t)$, jeweils mit $\Delta t/T_0 = 0.25$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Fourierreihe.
- Eine kompakte Zusammenfassung der Thematik finden Sie in den beiden Lernvideos
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- Die Spektralfunktion beinhaltet eine Diracfunktion bei $f = 0$ mit dem Gewicht $0.5$ (Gleichanteil) sowie weitere Spektrallinien bei ungeradzahligen Vielfachen ($n = \pm1, \pm3, \pm5,...$) von $f_0$.
- Die Gewichte bei $\pm f_0$ sind jeweils $A_1/2 = 1/\pi = 0.318$.
'(2) Richtig sind die Aussagen 1, 2 und 4:
- Bei allen ungeradzahligen Vielfachen der Grundfrequenz existieren Spektrallinien, zusätzlich noch bei den $2–{\rm fachen}$, $6–{\rm fachen}$ und $10–{\rm fachen}$.
- Beispielsweise gilt $A_1 = 1/\pi = 0.450$. ????? Die Spektrallinie bei $2f_0$ hat somit das Gewicht $A_2/2 = 1/(2\pi) = 0.159$.
- Beispielsweise gilt $A_2 = 1/\pi = 0.318$. Die Spektrallinie bei $2f_0$ hat somit das Gewicht $A_2/2 = 1/(2\pi) = 0.159$.
- Für $n = 4$, $n = 8$, usw. sind dagegen die Koeffizienten $A_n = 0$, da für die Sinusfunktion gilt: $\sin(\pi) = \sin(2\pi) = ... = 0$.
'(3) Aus der grafischen Darstellung des Signals ${y(t)}$ wird deutlich, dass $A_0 = 0.75$ gelten muss. Zum gleichen Ergebnis kommt man über die Beziehung:
- $$A_0^{(y)}=1-A_0^{(x)}=1-0.25\hspace{0.15cm}\underline{=0.75}.$$
'(4) Es gilt ${y(t)} = 1 – x(t)$. Für $n \neq 0$ ergeben sich somit die gleichen Fourierkoeffizienten wie für das Signal $x(t)$, jedoch mit negativen Vorzeichen. Inbesondere gilt:
- $$A_1^{(y)} = -A_1^{(x)}=-{2}/{\pi} \cdot \sin({\pi}/{4})= -{\sqrt2}/{\pi}\hspace{0.15cm}\underline{\approx -0.450},$$
- $$A_2^{(y)} = -A_2^{(x)}=-{1}/{\pi}\hspace{0.15cm}\underline{ \approx - 0.318}.$$
'(5) Es gilt ${z(t)} = y(t – T_0/2)$. Mit der Fourierreihendarstellung von ${y(t)}$ folgt daraus:
- $$z(t)=A_0+A_1^{(y)}\cos(\omega_0(t-\frac{T_0}{2}))+A_2^{(y)}\cos(2\omega_0(t-\frac{T_0}{2}))+A_3^{(y)}\cos(3\omega_0(t-\frac{T_0}{2}))+\ldots$$
- $$\Rightarrow \quad z(t)=A_0-A_1^{(y)}\cos(\omega_0 t)+A_2^{(y)}\cos(2\omega_0 t)-A_3^{(y)}\cos(3\omega_0 t)+\ldots$$
Damit erhält man:
- $$A_1^{(z)}=-A_1^{(y)}={\sqrt2}/{\pi}\hspace{0.15cm}\underline{=+0.450}, \hspace {0.5cm} A_2^{(z)}=A_2^{(y)}=-{1}/{\pi}\hspace{0.15cm}\underline{=-0.318}.$$
Das gleiche Ergebnis erhält man ausgehend von den gegebenen Koeffizienten mit $\Delta t/T_0 = 0.75$:
- $$A_1^{(z)}={2}/{\pi} \cdot \sin({3}/{4}\cdot \pi)={\sqrt2}/{\pi}, \hspace {0.5cm}A_2^{(z)}= {1}/{\pi} \cdot \sin({3}/{2} \cdot \pi) =-{1}/{\pi}.$$