Stochastische Signaltheorie/Weitere Verteilungen: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
|||
| Zeile 33: | Zeile 33: | ||
:$$x=\sqrt{u^2+v^2}.$$ | :$$x=\sqrt{u^2+v^2}.$$ | ||
| − | [[Datei:P_ID62__Sto_T_3_7_S1_neu.png |right| Mustersignal und WDF einer rayleighverteilten Zufallsgröße|class=fit]] | + | [[Datei:P_ID62__Sto_T_3_7_S1_neu.png |right|frame| Mustersignal und WDF einer rayleighverteilten Zufallsgröße|class=fit]] |
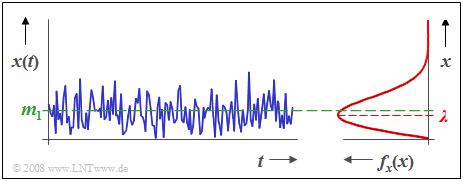
{{Beispiel}}''':''' Die Grafik zeigt den Zeitverlauf $x(t)$ einer rayleighverteilten Zufallsgröße sowie die zugehörige Dichtefunktion $f_{x}(x)$. | {{Beispiel}}''':''' Die Grafik zeigt den Zeitverlauf $x(t)$ einer rayleighverteilten Zufallsgröße sowie die zugehörige Dichtefunktion $f_{x}(x)$. | ||
| Zeile 59: | Zeile 59: | ||
:$$x=\sqrt{u^2+v^2}\hspace{0.5cm}{\rm mit}\hspace{0.5cm}m_u + m_v > 0 .$$ | :$$x=\sqrt{u^2+v^2}\hspace{0.5cm}{\rm mit}\hspace{0.5cm}m_u + m_v > 0 .$$ | ||
| − | [[Datei:P_ID63__Sto_T_3_7_S2_neu.png |right| Mustersignal und WDF einer riceverteilten Zufallsgröße]] | + | [[Datei:P_ID63__Sto_T_3_7_S2_neu.png |right|frame| Mustersignal und WDF einer riceverteilten Zufallsgröße]] |
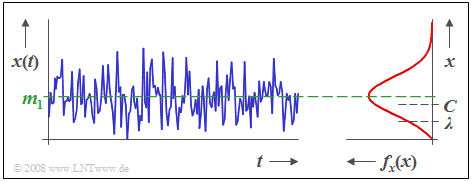
{{Beispiel}}''':''' Die Grafik zeigt den zeitlichen Verlauf einer riceverteilten Zufallsgröße $x$ sowie deren Dichtefunktion $f_{\rm x}(x)$, wobei $C/λ =$ 2 gilt. | {{Beispiel}}''':''' Die Grafik zeigt den zeitlichen Verlauf einer riceverteilten Zufallsgröße $x$ sowie deren Dichtefunktion $f_{\rm x}(x)$, wobei $C/λ =$ 2 gilt. | ||
| Zeile 88: | Zeile 88: | ||
:$$x=\lambda \cdot {\tan}( {\pi}/{2}\cdot u).$$ | :$$x=\lambda \cdot {\tan}( {\pi}/{2}\cdot u).$$ | ||
| − | [[Datei:P_ID64__Sto_T_3_7_S3_neu.png |right| WDF einer cauchyverteilten Zufallsgröße]] | + | [[Datei:P_ID64__Sto_T_3_7_S3_neu.png |right|frame| WDF einer cauchyverteilten Zufallsgröße]] |
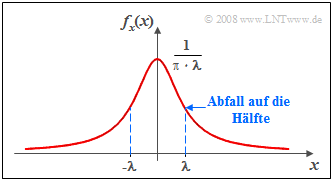
{{Beispiel}}''':''' Die Grafik zeigt die Cauchy-WDF. | {{Beispiel}}''':''' Die Grafik zeigt die Cauchy-WDF. | ||
| Zeile 102: | Zeile 102: | ||
Bei einer Zufallsgröße $x$ mit bekannter WDF $f_{x}(x)$ und VTF $F_{x}(r)$ kann die Wahrscheinlichkeit, dass die Zufallsgröße $x$ betragsmäßig um mehr als einen Wert $ε$ von ihrem Mittelwert $m_{x}$ abweicht, entsprechend der in diesem Kapitel allgemein beschriebenen Weise exakt berechnet werden. | Bei einer Zufallsgröße $x$ mit bekannter WDF $f_{x}(x)$ und VTF $F_{x}(r)$ kann die Wahrscheinlichkeit, dass die Zufallsgröße $x$ betragsmäßig um mehr als einen Wert $ε$ von ihrem Mittelwert $m_{x}$ abweicht, entsprechend der in diesem Kapitel allgemein beschriebenen Weise exakt berechnet werden. | ||
| − | [[Datei:P_ID623__Sto_T_3_7_S4_ganz_neu.png | Tschebyscheffsche Ungleichung | rechts]] | + | [[Datei:P_ID623__Sto_T_3_7_S4_ganz_neu.png |frame| Tschebyscheffsche Ungleichung | rechts]] |
*Ist neben dem Mittelwert $m_{x}$ zwar noch die Streuung $σ_{x}$ bekannt, nicht jedoch der exakte WDF-Verlauf $f_{x}(x)$, so lässt sich für diese Wahrscheinlichkeit zumindest eine obere Schranke angeben: | *Ist neben dem Mittelwert $m_{x}$ zwar noch die Streuung $σ_{x}$ bekannt, nicht jedoch der exakte WDF-Verlauf $f_{x}(x)$, so lässt sich für diese Wahrscheinlichkeit zumindest eine obere Schranke angeben: | ||
:$${\rm Pr}(|x - m_{\rm x}|\ge\varepsilon)\le\frac{\sigma_{x}^{\rm 2}}{\varepsilon^{\rm 2}}. $$ | :$${\rm Pr}(|x - m_{\rm x}|\ge\varepsilon)\le\frac{\sigma_{x}^{\rm 2}}{\varepsilon^{\rm 2}}. $$ | ||
Version vom 28. Dezember 2017, 19:48 Uhr
Inhaltsverzeichnis
Rayleighverteilung
$$f_{x}(x)=\frac{x}{\lambda^2}\cdot {\rm e}^{-{x^{\rm 2}} /{({\rm 2} \lambda^{\rm 2})}}.$$
Der Name geht auf den englischen Physiker John William Strutt zurück, dem „ dritten Baron Rayleigh”. 1904 erhielt er den Physik-Nobelpreis.
- Diese Verteilung spielt für die Beschreibung zeitvarianter Kanäle eine zentrale Rolle. Solche Kanäle werden beispielweise im Buch Mobile Kommunikation beschrieben.
- So weist „nichtfrequenzselektives Fading„ eine solche Verteilung auf, wenn zwischen der festen Basisstation und dem mobilen Teilnehmer keine Sichtverbindung besteht.
Die Rayleighverteilung besitzt folgende charakteristische Eigenschaften:
- Eine rayleighverteilte Zufallsgröße $x$ kann keine negativen Werte annehmen und der theoretisch mögliche Wert $x = 0$ tritt auch nur mit der Wahrscheinlichkeit $0$ auf.
- Das $k$-te Moment einer rayleighverteilten Zufallsgröße $x$ ergibt sich allgemein zu
- $$m_k=(2\cdot \lambda^{\rm 2})^{\it k/\rm 2}\cdot {\rm \Gamma}( 1+ {\it k}/{\rm 2}) \hspace{0.3cm}{\rm mit }\hspace{0.3cm}{\rm \Gamma}(x)= \int_{0}^{\infty} t^{x-1} \cdot {\rm e}^{-t} \hspace{0.1cm}{\rm d}t.$$
- Daraus lassen sich der Mittelwert $m_1$ und die Streuung $\sigma_1$ folgendermaßen berechnen:
- $$m_1=\sqrt{2}\cdot \lambda\cdot {\rm \Gamma}(1.5) = \sqrt{2}\cdot \lambda\cdot {\sqrt{\pi}}/{2} =\lambda\cdot\sqrt{{\pi}/{2}},$$
- $$m_2=2 \lambda^2 \cdot {\rm \Gamma}(2) = 2 \lambda^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma = \sqrt{m_2 - m_1^2} =\lambda\cdot\sqrt{2-{\pi}/{2}}.$$
- Zur Modellierung einer rayleighverteilten Zufallsgröße $x$ verwendet man zum Beispiel zwei gaußverteilte, mittelwertfreie und statistisch unabhängige Zufallsgrößen $u$ und $v$, die beide die Streuung $σ = λ$ aufweisen. Die Größen $u$ und $v$ werden dann wie folgt verknüpft:
- $$x=\sqrt{u^2+v^2}.$$
Man erkennt aus dieser Darstellung:
- Die Rayleigh-WDF ist stets unsymmetrisch.
- Der Mittelwert $m_1$ liegt etwa 25% oberhalb des WDF-Maximums, das bei $x = λ$ auftritt.
Riceverteilung
$$f_{\rm x}(x)=\frac{x}{\lambda^2}\cdot{\rm e}^{-({C^2+\it x^{\rm 2}})/ ({\rm 2 \it \lambda^{\rm 2}})}\cdot {\rm I_0}(\frac{\it x\cdot C}{\lambda^{\rm 2}}) \hspace{0.4cm}{\rm mit} \hspace{0.4cm} {\rm I_0}(x) = \sum_{k=0}^{\infty}\frac{(x/2)^{2k}}{k! \cdot {\rm \Gamma ({\it k}+1)}}.$$ ${\rm I_0}( ... )$ bezeichnet die modifizierte Besselfunktion nullter Ordnung.
Der Name geht auf den Mathematiker und Logiker Henry Gordon Rice zurück. Er lehrte als Professor der Mathematik an der University of New Hampshire.
Auch diese Verteilung spielt für die Beschreibung zeitvarianter Kanäle eine wichtige Rolle, unter Anderem auch deshalb, weil nichtfrequenzselektives Fading dann riceverteilt ist, wenn zwischen der Basisstation und dem Mobilteilnehmer eine Sichtverbindung besteht.
Für die Riceverteilung gelten folgende Aussagen:
- Der gegenüber der Rayleighverteilung zusätzliche Parameter $C$ ist ein Maß für die „Stärke” der Direktkomponente. Je größer der Quotient $C/λ$ ist, desto mehr nähert sich der Ricekanal dem Gauß-Kanal an. Für $C = 0$ geht die Riceverteilung in die Rayleighverteilung über.
- Bei der Riceverteilung ist der Ausdruck für das Moment $m_k$ deutlich komplizierter und nur mit Hilfe hypergeometrischer Funktionen angebbar. Ist jedoch $λ$ sehr viel kleiner als $C$, so gilt $m_1 ≈ C$ und $σ ≈ λ$. Unter diesen Voraussetzungen kann die Riceverteilung durch eine Gaußverteilung mit Mittelwert $C$ und Streuung $λ$ angenähert werden.
- Zur Modellierung einer riceverteilten Zufallsgröße $x$ verwenden wir ein ähnliches Modell wie für die Rayleighverteilung, nur muss nun zumindest eine der beiden gaußverteilten und statistisch voneinander unabhängigen Zufallsgrößen $(u$ und/oder $v$) einen Mittelwert ungleich 0 aufweisen.
- $$x=\sqrt{u^2+v^2}\hspace{0.5cm}{\rm mit}\hspace{0.5cm}m_u + m_v > 0 .$$
- Etwas salopp ausgedrückt: Die Riceverteilung ist ein Kompromiss zwischen der Rayleigh- und der Gaußverteilung.
- Der Mittelwert $m_1$ ist hier etwas größer als $C$.
Mit dem Berechnungstool WDF, VTF und Momente spezieller Verteilungen können Sie sich unter Anderem die Kenngrößen (WDF, VTF, Momente) der Rayleigh- und der Riceverteilung anzeigen lassen.
Cauchyverteilung
$$f_{x}(x)=\frac{1}{\pi}\cdot\frac{\lambda}{\lambda^2+x^2}, \hspace{2cm} F_{x}(r)={\rm 1}/{2}+{\rm arctan}({r}/{\lambda}).$$ Manchmal wird in der Literatur auch noch ein Mittelwert $m_1$ berücksichtigt.
Der Name geht auf den französischen Mathematiker Augustin-Louis Cauchy zurück, der als ein Pionier der Analysis die von Gottfried Wilhelm Leibniz und Sir Isaac Newton aufgestellten Grundlagen weiterentwickelte und deren fundamentale Aussagen auch formal bewies. Insbesondere in der Funktionentheorie stammen viele zentrale Sätze von ihm.
Die Cauchyverteilung hat weniger praktische Bedeutung, ist mathematisch aber sehr interessant. Sie weist mit $m_1 = 0$ folgende Eigenschaften auf:
- Bei der Cauchyverteilung besitzen alle Momente $m_k$ für gerades $k$ einen unendlich großen Wert, und zwar unabhängig vom Parameter $λ$. Aufgrund der Symmetrie sind für ungerades $k$ alle Momente $m_k = 0$.
- Damit besitzt diese Verteilung auch eine unendlich große Varianz $\sigma^2 = m_2$ ⇒ Leistung. Deshalb ist es offensichtlich, dass keine physikalische Größe cauchyverteilt sein kann.
- Der Quotient $u/v$ zweier unabhängiger gaußverteilter mittelwertfreier Größen $u$ und $v$ ist mit dem Verteilungsparameter $λ = σ_u/σ_v$ cauchyverteilt.
- Eine cauchyverteilte Zufallsgröße $x$ lässt sich aus einer zwischen $–1$ und $+1$ gleichverteilten Größe $u$ erzeugen, wenn man die folgende nichtlineare Transformation durchführt:
- $$x=\lambda \cdot {\tan}( {\pi}/{2}\cdot u).$$
- Zu erkennen ist der langsame Abfall dieser Funktion zu den Rändern hin.
- Da dieser asymptotisch mit $1/x^2$ erfolgt, sind die Varianz und die Momente höherer Ordnung (mit geradzahligem Index) unendlich groß.
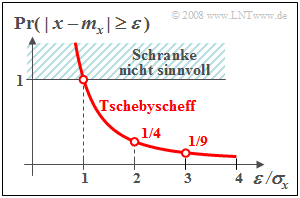
Tschebyscheffsche Ungleichung
Bei einer Zufallsgröße $x$ mit bekannter WDF $f_{x}(x)$ und VTF $F_{x}(r)$ kann die Wahrscheinlichkeit, dass die Zufallsgröße $x$ betragsmäßig um mehr als einen Wert $ε$ von ihrem Mittelwert $m_{x}$ abweicht, entsprechend der in diesem Kapitel allgemein beschriebenen Weise exakt berechnet werden.
- Ist neben dem Mittelwert $m_{x}$ zwar noch die Streuung $σ_{x}$ bekannt, nicht jedoch der exakte WDF-Verlauf $f_{x}(x)$, so lässt sich für diese Wahrscheinlichkeit zumindest eine obere Schranke angeben:
- $${\rm Pr}(|x - m_{\rm x}|\ge\varepsilon)\le\frac{\sigma_{x}^{\rm 2}}{\varepsilon^{\rm 2}}. $$
- Diese von Pafnuti L. Tschebyscheff angegebene Schranke – bekannt als „Tschebyscheffsche Ungleichung” – ist im Allgemeinen allerdings nur eine sehr grobe Näherung für die tatsächliche Überschreitungswahrscheinlichkeit.
- Sie sollte deshalb nur bei unbekanntem Verlauf der WDF $f_{x}(x)$ angewendet werden.
- Damit ist die Wahrscheinlichkeit, dass deren Betrag $|x|$ größer als die 3-fache Streuung $(3 · σ_{x})$ ist, einfach berechenbar und ergibt den Wert ${\rm 2 · Q(3) ≈ 2.7 · 10^{–3}}.$
- Die Tschebyscheffsche Ungleichung liefert hier als eine obere Schranke den deutlich zu großen Wert $1/9 ≈ 0.111$, die aber für jede beliebige WDF–Form ebenfalls gelten würde.
Aufgaben zum Kapitel
Zusatzaufgabe 3.10Z: Rayleigh? Oder Rice?
Aufgabe 3.11: Tschebyscheffsche Ungleichung
Aufgabe 3.12: Cauchyverteilung