Kanalcodierung/Schranken für die Blockfehlerwahrscheinlichkeit: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
|||
| Zeile 276: | Zeile 276: | ||
== Aufgaben zum Kapitel == | == Aufgaben zum Kapitel == | ||
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.14:_Bhattacharyya–Schranke_für_BEC|Aufgabe 1.14: Bhattacharyya–Schranke für BEC]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.15:_Distanzspektren_von_HC_(7,_4,_3)_und_HC_(8,_4,_4)|Aufgabe 1.15: Distanzspektren von HC (7, 4, 3) und HC (8, 4, 4)]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.16:_Fehlerwahrscheinlichkeitsschranken_für_AWGN|Aufgabe 1.16: Fehlerwahrscheinlichkeitsschranken für AWGN]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.16Z:_Schranken_für_die_Gaußsche_Fehlerfunktion|Aufgabe 1.16Z: Schranken für die_Gaußsche Fehlerfunktion]] |
{{Display}} | {{Display}} | ||
Version vom 5. Januar 2018, 17:40 Uhr
Inhaltsverzeichnis
Distanzspektrum eines linearen Codes
Wir gehen weiterhin von einem linearen und binären $(n, \hspace{0.05cm} k)$–Blockcode $\mathcal{C}$ aus. Ein wesentliches Ziel des Codedesigns ist es, die Blockfehlerwahrscheinlichkeit ${\rm Pr}(\underline{u} \ne \underline{v}) = {\rm Pr}(\underline{z} \ne \underline{x})$ möglichst gering zu halten. Dies erreicht man unter anderem dadurch, dass
- die minimale Distanz $d_{\rm min}$ zwischen zwei Codeworten $\underline{x}$ und $\underline{x}'$ möglichst groß ist, so dass man bis zu $t = ⌊(d_{\rm min}-1)/2⌋$ Bitfehler richtig korrigieren kann;
- gleichzeitig die minimale Distanz $d_{\rm min}$ ⇒ worst–case möglichst selten auftritt, wenn man alle zulässigen Codeworte berücksichtigt.
$\text{Definition:}$ Wir benennen die Anzahl der Codeworte $\underline{x}' \in \mathcal{C}$ mit der Hamming–Distanz $i$ vom betrachteten Codewort $\underline{x}$ des gleichen Codes $\mathcal{C}$ mit $W_i(\underline{x})$, wobei gilt:
- \[W_i(\underline{x}) = \left \vert \hspace{0.05cm} \left \{ \underline{x} \hspace{0.05cm}, \underline{x}{\hspace{0.03cm}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm}\vert\hspace{0.1cm} d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}' ) = i \right \} \hspace{0.05cm} \right \vert\hspace{0.05cm}.\]
- Die Betragsstriche kennzeichnen hierbei die Anzahl der Codeworte $\underline{x}'$, die die Bedingung $d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}' ) = i $ erfüllen.
- Man bezeichnet diesen Wert auch als Vielfachheit (englisch: Multiplicity).
$\text{Beispiel 1:}$ Wir betrachten den $(5, \, 2)$–Blockcode $\mathcal{C}$ mit der Generatormatrix
\[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 &0 &1 &1 &0 \\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.\]
Die Tabelle zeigt die Hamming–Distanzen zwischen allen Codeworten $\underline{x}_i$ zu den Bezugsworten $\underline{x}_0$, ... , $\underline{x}_3$.
Man erkennt, dass unabhängig vom Bezugswort $\underline{x}_i$ gilt:
- \[W_0 = 1 \hspace{0.05cm}, \hspace{0.5cm}W_1 = W_2 = 0 \hspace{0.05cm},\]
- \[ W_3 = 2 \hspace{0.05cm},\hspace{0.5cm} W_4 = 1\]
- \[ \Rightarrow\hspace{0.3cm} d_{\rm min} = 3\hspace{0.05cm}.\]
Nicht nur in diesem Beispiel, sondern bei jedem linearen Code ergeben sich für jedes Codewort die gleichen Vielfachheiten $W_i$. Da zudem das Nullwort $\underline{0} = (0, 0,\text{ ...} \hspace{0.05cm}, 0)$ Bestandteil eines jeden linearen Binärcodes ist, lässt sich die obige Definition auch wie folgt formulieren:
$\text{Definition:}$ Das Distanzspektrum eines linearen binären $(n, \hspace{0.03cm} k)$–Blockcodes ist die Menge $\{W_i \}$ mit $i = 0, 1,$ ... , $n$. Hierbei gibt $W_i$ die Anzahl der Codeworte $\underline{x} \in \mathcal{C}$ mit Hamming–Gewicht $w_{\rm H}(\underline{x}) = i$ an.
Oft beschreibt man die Menge $\hspace{0.05cm}\{W_i \}\hspace{0.05cm}$ auch als Polynom mit einer Pseudovariablen $X$:
- \[\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} W(X) = \sum_{i=0 }^{n} W_i \cdot Xi^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.\]
Man bezeichnet $W(X)$ auch als Gewichtsfunktion (englisch: Weight Enumerator Function, WEF).
Beispielsweise lautet die Gewichtsfunktion des $(5, \hspace{0.02cm} 2)$–Codes $\mathcal{C} = \left \{ \hspace{0.05cm}(0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \hspace{0.05cm} \right \}$ von Beispiel 1:
- \[W(X) = 1 + 2 \cdot X^{3} + X^{4}\hspace{0.05cm}.\]
Wie aus der Tabelle seiner Codeworte hervorgeht, erhält man für den $(7, \hspace{0.02cm}4, \hspace{0.02cm}3)$–Hamming–Code:
- \[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.\]
Die Überführung des Distanzspektrums $\hspace{0.01cm}\{W_i \}\hspace{0.01cm}$ in die Gewichtsfunktion $W(X)$ bietet zudem bei manchen Aufgabenstellungen große numerische Vorteile. Ist beispielsweise die Weight Enumerator Function $W(X)$ eines $(n, \hspace{0.03cm} k)$–Blockcodes $\mathcal{C}$ bekannt, so gilt für den hierzu dualen $(n, \hspace{0.03cm} n-k)$–Code $\mathcal{C}_{\rm Dual}$:
- \[W_{\rm Dual}(X) = \frac{(1+X)^n}{2^k} \cdot W \left ( \frac{1-X}{1+X} \right )\hspace{0.05cm}.\]
$\text{Beispiel 2:}$ Gesucht ist die Gewichtsfunktion $W(X)$ des Single Parity–check Codes mit $n = 6$, $k = 5$ ⇒ SPC (6, 5). Man erhält diese durch Vergleich aller $2^5 = 32$ Codeworte mit dem Nullwort:
- \[W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = 1 + 15 \cdot X^{2} + 15 \cdot X^{4} + X^{6}\hspace{0.05cm}.\]
Unter Berücksichtigung obiger Gleichung kommt man sehr viel schneller zum gleichen Ergebnis:
- Der zu SPC (6, 5) duale Code ist der Repetition Code RC (6, 1) mit nur zwei Codeworten $(0, 0, 0, 0, 0, 0)$ und $(1, 1, 1, 1, 1, 1)$:
- \[W_{\rm RC\hspace{0.03cm}(6,\hspace{0.08cm}1)}(X) = 1 + X^{6}\hspace{0.05cm}.\]
- Daraus folgt für die Gewichtsfunktion des SPC (6, 5) nach obiger Gleichung mit $k = 1$:
- \[W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = \frac{(1+X)^6}{2^1} \cdot W \left [1 + \left ( (1-X)/(1+X)\right )^6 \right ] = 1/2 \cdot \left [( 1+X) ^6 + ( 1-X) ^6 \right ] = 1 + 15 \cdot X^{2} + 15 \cdot X^{4} + X^{6}\hspace{0.05cm}.\]
Union Bound der Blockfehlerwahrscheinlichkeit
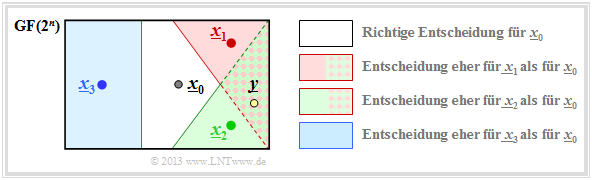
Wir betrachten wie im Beispiel 1 zum Distanzspektrum] den $(5, \hspace{0.02cm} 2)$–Blockcode $\mathcal{C} = (\underline{x}_0, \underline{x}_1, \underline{x}_2, \underline{x}_3)$ und setzen voraus, dass das Codewort $\underline{x}_0$ gesendet wurde. Die Grafik verdeutlicht den Sachverhalt).
Im fehlerfreien Fall würde dann der Codewortschätzer $\underline{z} = \underline{x}_0$ liefern. Andernfalls käme es zu einem Blockfehler (das heißt $\underline{z} \ne \underline{x}_0$ und dementsprechend $\underline{v} \ne \underline{u}_0$ mit der Wahrscheinlichkeit
- \[{\rm Pr(Blockfehler)} = {\rm Pr}\left ([\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \right ) \hspace{0.05cm}.\]
Das Ereignis „Verfälschung von $\underline{x}_0$ nach $\underline{x}_1$” tritt für ein gegebenes Empfangswort $\underline{y}$ entsprechend der Maximum–Likelihood–Entscheidungsregel (block–wise ML) genau dann ein, wenn für die bedingte Wahrscheinlichkeitsdichtefunktion gilt:
- \[[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.3cm} \Longleftrightarrow \hspace{0.3cm} f(\underline{x}_{\hspace{0.02cm}0}\hspace{0.02cm} | \hspace{0.05cm}\underline{y}) < f(\underline{x}_{\hspace{0.02cm}1}\hspace{0.02cm} | \hspace{0.05cm}\underline{y}) \hspace{0.05cm}.\]
Da $[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] $, $[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] $, $[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] $nicht notwendigerweise disjunkte Ereignisse sind (die sich somit gegenseitig ausschließen würden), ist die Wahrscheinlichkeit der Vereinigungsmenge kleiner oder gleich der Summe der Einzelwahrscheinlichkeiten:
\[{\rm Pr(Blockfehler)} \le {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}+\hspace{0.05cm}{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}+ \hspace{0.05cm}{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \hspace{0.05cm}.\]
Man nennt diese obere Schranke für die (Block–)Fehlerwahrscheinlichkeit die Union Bound. Diese wurde bereits im Kapitel Approximation_der_Fehlerwahrscheinlichkeit des Buches „Digitalsignalübertragung” verwendet.
Verallgemeinern und formalisieren wir diese Ergebnisse unter der Voraussetzung, dass sowohl $\underline{x}$ als auch $\underline{x}'$ zum Code $\mathcal{C}$ gehören. Dann gelten folgende Berechnungsvorschriften:
$\text{Definitionen:}$
- Blockfehlerwahrscheinlichkeit:
- \[{\rm Pr(Blockfehler)} = {\rm Pr} \left ( \bigcup_{\underline{x}' \ne \underline{x} } \hspace{0.15cm} [\underline{x} \mapsto \underline{x}'] \right )\hspace{0.05cm},\]
- Obere Schranke nach der Union Bound:
- \[{\rm Pr(Union \hspace{0.15cm}Bound)} \le \sum_{\underline{x}' \ne \underline{x} } \hspace{0.15cm} {\rm Pr}[\underline{x} \mapsto \underline{x}'] \hspace{0.05cm},\]
- Paarweise Fehlerwahrscheinlichkeit (nach dem MAP– bzw. ML–Kriterium):
- \[{\rm Pr}\hspace{0.02cm}[\underline{x} \mapsto \underline{x}'] = {\rm Pr} \left [ f(\underline{x}\hspace{0.05cm}\vert \hspace{0.05cm}\underline{y}) \le f(\underline{x}'\hspace{0.05cm} \vert \hspace{0.05cm}\underline{y}) \right ] \hspace{0.05cm}.\]
Auf den nächsten Seiten werden diese Ergebnisse auf verschiedene Kanäle angewendet.
Union Bound für das BSC–Modell
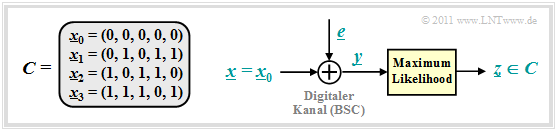
Wir betrachten weiterhin den beispielhaften $(5, \hspace{0.02cm} 2)$–Code: $\mathcal{C} = \left \{ \hspace{0.05cm}(0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \hspace{0.05cm} \right \}$ und für den digitalen Kanal verwenden wir das BSC–Modell (Binary Symmetric Channel):
- \[{\rm Pr}(y = 1 \hspace{0.05cm} | \hspace{0.05cm}x = 0 ) \hspace{-0.15cm} = {\rm Pr}(y = 0 \hspace{0.05cm} | \hspace{0.05cm}x = 1 ) = {\rm Pr}(e = 1) = \varepsilon \hspace{0.05cm},\]
- \[{\rm Pr}(y = 0 \hspace{0.05cm} | \hspace{0.05cm}x = 0 ) \hspace{-0.15cm} = {\rm Pr}(y = 1 \hspace{0.05cm} | \hspace{0.05cm}x = 1 ) = {\rm Pr}(e = 0) = 1 -\varepsilon \hspace{0.05cm}.\]
Dann gilt:
- Die beiden Codeworte $\underline{x}_0 = (0, 0, 0, 0, 0)$ und $\underline{x}_1 = (0, 1, 0, 1, 1)$ unterscheiden sich in genau $d = 3$ Bitpositionen, wobei $d$ die Hamming–Distanz zwischen $\underline{x}_0$ und $\underline{x}_1$ angibt.
- Ein falsches Decodierergebnis $[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] $ erhält man immer dann, wenn mindestens zwei der drei Bit an den Bitpositionen 2, 4 und 5 verfälscht werden.
- Die Bitpositionen 1 und 3 spielen hier dagegen keine Rolle, da diese für $\underline{x}_0$ und $\underline{x}_1$ gleich sind.
Da der betrachtete Code $t = ⌊(d-1)/2⌋ = 1$ Fehler korrigieren kann, gilt:
- \[{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i=t+1 }^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} = {3 \choose 2} \cdot \varepsilon^{2} \cdot (1 - \varepsilon) + {3 \choose 3} \cdot \varepsilon^{3} =3 \cdot \varepsilon^2 \cdot (1 - \varepsilon) + \varepsilon^3 = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}]\hspace{0.05cm}.\]
Hierbei ist berücksichtigt, dass sich $\underline{x}_0 = (0, 0, 0, 0, 0)$ und $\underline{x}_2 = (1, 0, 1, 1, 0)$ ebenfalls in drei Bitpositionen unterscheiden.
Die Codeworte $\underline{x}_0 = (0, 0, 0, 0, 0)$ und $\underline{x}_3 = (1, 1, 1, 0, 1)$ unterscheiden sich dagegen in vier Bitpositionen:
- Zu einer falschen Decodierung des Blocks kommt es deshalb mit Sicherheit, wenn vier oder drei Bit verfälscht werden.
- Eine Verfälschung von zwei Bit hat mit 50–prozentiger Wahrscheinlichkeit ebenfalls einen Blockfehler zur Folge, wenn man hierfür eine Zufallsentscheidung voraussetzt.
- \[{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] = \varepsilon^4 + 4 \cdot \varepsilon^3 \cdot (1 - \varepsilon) + {1}/{2} \cdot 6 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^2 \hspace{0.05cm}.\]
Daraus ergibt sich für die „Union Bound”:
\[{\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(Blockfehler)} .\]
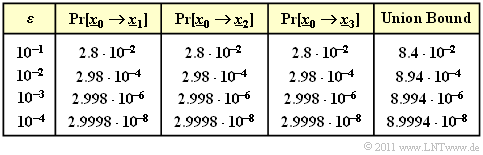
$\text{Beispiel 3:}$ In der Tabelle sind die Ergebnisse für verschiedene Werte des BSC–Parameters $\varepsilon$ zusammengefasst.
Zu erwähnen ist, dass die völlig unterschiedlich zu berechnenden Wahrscheinlichkeiten ${\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}]$ und ${\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}3}]$ genau das gleiche Ergebnis liefern.
Die obere Schranke nach Bhattacharyya
Eine weitere obere Schranke für die Blockfehlerwahrscheinlichkeit wurde von Bhattacharyya angegeben:
- \[{\rm Pr(Blockfehler)} \le W(X = \beta) -1 = {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]
Hierzu ist anzumerken:
- $W(X)$ ist die oben definierte Gewichtsfunktion, die den verwendeten Kanalcode charakterisiert.
- Der Bhattacharyya–Parameter $\beta$ kennzeichnet den digitalen Kanal. Beispielsweise gilt:
- \[\beta = \left\{ \begin{array}{c} \lambda \\ \sqrt{4 \cdot \varepsilon \cdot (1- \varepsilon)}\\ {\rm exp}[- R \cdot E_{\rm B}/N_0] \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r\hspace{0.15cm} das \hspace{0.15cm}BEC-Modell},\\ {\rm f\ddot{u}r\hspace{0.15cm} das \hspace{0.15cm}BSC-Modell}, \\ {\rm f\ddot{u}r\hspace{0.15cm} das \hspace{0.15cm}AWGN-Modell}. \end{array}\]
- Die Bhattacharyya–Schranke liegt stets (und meist deutlich) oberhalb der Kurve für die „Union Bound”. Mit dem Ziel, eine für alle Kanäle einheitliche Schranke zu finden, müssen hier sehr viel gröbere Abschätzungen vorgenommen werden als für die Herleitung der „Union Bound”.
Wir beschränken uns hier auf die Bhattacharyya–Schranke für das BSC–Modell. Für dessen paarweise Verfälschungswahrscheinlichkeit wurde vorne hergeleitet:
- \[{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] = \sum_{i= \left\lfloor (d-1)/2 \right\rfloor}^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} = \sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i}\hspace{0.05cm}.\]
Hierbei kennzeichnet $\varepsilon = {\rm Pr}(y = 1\hspace{0.04cm}|\hspace{0.04cm} x = 0) = {\rm Pr}(y = 0\hspace{0.04cm}|\hspace{0.04cm} x = 1)< 0.5$ das Kanalmodell und $d = d_{\rm H}(\underline{x}_0,\, \underline{x}_1)$ gibt die Hamming–Distanz der betrachteten Codeworte an.
Um zur Bhattacharyya–Schranke zu kommen, müssen folgende Abschätzungen getroffen werden:
- Für alle$i < d$ gilt $\varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} \le (1 - \varepsilon)^{d/2}$:
- \[{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \le [\varepsilon \cdot (1 - \varepsilon)]^{d/2} \cdot \sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \hspace{0.05cm}.\]
- Änderung bezüglich der unteren Grenze der Laufvariablen $i$:
- \[\sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \hspace{0.15cm} < \hspace{0.15cm} \sum_{i= 0 }^{d} {d \choose i} = 2^d\hspace{0.05cm}, \hspace{0.2cm}\beta = 2 \cdot \sqrt{\varepsilon \cdot (1 - \varepsilon)} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] = \beta^{d} \hspace{0.05cm}.\]
- Umsortierung gemäß den Hamming–Gewichten $W_i$ (Hamming–Distanz $d = i$ kommt $W_i$ mal vor):
- \[{\rm Pr(Blockfehler)} \hspace{0.1cm} \le \hspace{0.1cm} \sum_{i= 1 }^{n} W_i \cdot \beta^{i} = 1 + W_1 \cdot \beta + W_2 \cdot \beta^2 + ... \hspace{0.05cm}+ W_n \cdot \beta^n \hspace{0.05cm}.\]
- Mit der Gewichtsfunktion $W(X)= 1 + W_1 \cdot X + W_2 \cdot X^2 + \text{...} + W_n \cdot X^n$:
- \[{\rm Pr(Blockfehler)} \le W(X = \beta) -1= {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]
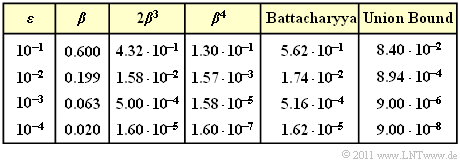
$\text{Beispiel 4:}$ In der Tabelle sind die Bhattacharyya–Ergebnisse für verschiedene Werte des BSC–Parameters $\varepsilon$ zusammengefasst, gültig für den beispielhaften (5, 2)–Code. Für diesen gilt:
- $$W_0 = 1, \ \ W_1 = W_2 = 0, \ \ W_3 = 2, \ \ W_4 = 1$$
- $$\Rightarrow\hspace{0.3cm} W(X) = 1 + 2 \cdot X^3 + X^4.$$
Damit kann die Bhattacharyya–Schranke berechnet werden:
- \[ {\rm Pr(Bhattacharyya)} = W(\beta) -1 = 2 \cdot \beta^3 + \beta^4\hspace{0.05cm}.\]
Diese stellt eine (oft grobe) Schranke für die Blockfehlerwahrscheinlichkeit dar:
- \[ {\rm Pr(Blockfehler)} \le {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]
$\text{Fazit:}$ Basierend auf Beispiel 3 und Beispiel 4 (auf dieser Seite) für den einfachen (5, 2)–Bolckcode, der allerdings wenig praxisrelevant ist, sowie im Vorgriff aufdas Beispiel 5 (auf der folgenden Seite) für den (7, 4, 3)–Hamming–Code kann man zusammenfassen:
- Die Blockfehlerwahrscheinlichkeit eines Codiersystems ist oft analytisch nicht angebbar und muss per Simulation ermittelt werden. Gleiches gilt für die Bitfehlerwahrscheinlichkeit.
- Die Union Bound liefert eine obere Schranke für die Blockfehlerwahrscheinlichkeit. Bei vielen Anwendungen (insbesondere bei kurzen Codes) liegt sie nur geringfügig über dieser.
- Die Bhattacharyya–Schranke liegt beim BEC–Kanal etwa um den Faktor 2 oberhalb der Union Bound – siehe Aufgabe 1.14. Beim BSC– und beim AWGN–Kanal ist der Abstand zwischen beiden Schranken deutlich größer. Der Faktor 10 (oder mehr) ist keine Seltenheit.
- Die Bhattacharyya–Schranke $W(\beta) - 1$ wirkt auf den ersten Blick sehr einfach. Es sind aber einige Vereinfachungsschritte erforderlich, um auf diese Form zu kommen. Trotzdem benötigt man auch hier Kenntnis über die genaue Gewichtsfunktion $W(\xi)$ des Codes.
- Bei Kenntnis des Übertragungskanals (BEC, BSC, AWGN oder Abwandlungen hiervon) und dessen Parameter spricht vom Aufwand her nichts dagegen, die Union Bound als obere Schranke für die Blockfehlerwahrscheinlichkeit zu verwenden.
Schranken für den (7, 4, 3)–Hamming–Code beim AWGN–Kanal
Abschließend betrachten wir die Blockfehlerwahrscheinlichkeit und deren Schranken (Union Bound und Bhattacharyya–Schranke) für die folgende Konfiguration:
- AWGN–Kanal, gekennzeichnet durch den Quotienten $E_{\rm B}/N_0$,
- Hamming–Code (7, 4) ⇒ $R = 4/7$, $W(X)-1 = – 1 = 7 \cdot X^3 + 7 \cdot X^4 + X^7$,
- Soft–Decision nach dem ML–Kriterium.
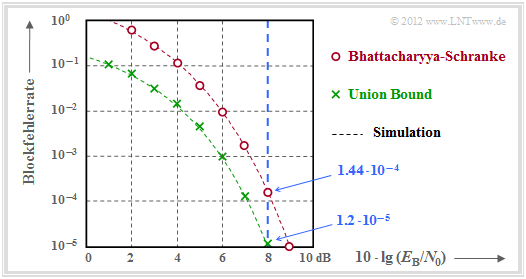
$\text{Beispiel 5:}$ Die Ergebnisse sind in der Grafik zusammengefasst.
- Im Gegensatz zur Grafik im Abschnitt Codiergewinn – Bitfehlerrate bei AWGN ist hier die Blockfehlerrate angegeben und nicht die Bitfehlerrate.
- Näherungsweise ist Letztere um den Faktor $d_{\rm min}/k$ kleiner, falls wie hier $d_{\rm min}< k$ ist. Im vorliegenden Beispiel gilt $d_{\rm min}/k = 0.75$.
- Berechnet wurden nur die Punkte für ganzzahlige dB–Werte. Die gestrichelten Linien wurden interpoliert.
- Die rechts angegebenen (blauen) Zahlenwerte gelten für $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$ ⇒ $E_{\rm B}/N_0 \approx 6.31$ (blaue Vertikale).
Die grünen Kreuze markieren die Union Bound. Nach dieser gilt:
- \[{\rm Pr(Blockfehler)} \le \sum_{i= d_{\rm min} }^{n} W_i \cdot {\rm Q} \left ( \sqrt{i \cdot {2R \cdot E_{\rm B} }/{N_0} } \right ) = 7 \cdot {\rm Q} (4.65) + 7 \cdot {\rm Q} (5.37) + {\rm Q} (7.10) \]
- \[\Rightarrow \hspace{0.3cm} {\rm Pr(Blockfehler)} \approx 7 \cdot 1.66 \cdot 10^{-6} + 7 \cdot 3.93 \cdot 10^{-8}+ 10^{-9} = 1.2 \cdot 10^{-5} \hspace{0.05cm}.\]
- Die Zahlenwerte machen deutlich, dass die Union Bound durch den ersten Term bestimmt wird:
- \[{\rm Pr(Union\hspace{0.15cm} Bound)} \approx W_{d_{\rm min} } \cdot {\rm Q} \left ( \sqrt{d_{\rm min} \cdot {2R \cdot E_{\rm B} }/{N_0} } \right ) = 1.16 \cdot 10^{-5} \hspace{0.05cm}.\]
- Allerdings ist diese so genannte Truncated Union Bound nicht mehr bei allen Anwendungen eine echte Schranke für die Blockfehlerwahrscheinlichkeit, sondern ist als Näherung zu verstehen.
- Die Bhattacharyya–Schranke ist in der Grafik durch rote Punkte markiert. Diese Schranke liegt aufgrund der stark vereinfachten Chernoff–Rubin Bound ${\rm Q}(x) \le {\rm e}^{-x^2/2}$ deutlich über der Union Bound.
- Für $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$ erhält man mit $\beta = {\rm e}^{-R \hspace{0.03cm}\cdot \hspace{0.03cm}E_{\rm B}/N_0} \approx 0.027$:
- \[{\rm Pr(Bhattacharyya)} = W(\beta) -1 = 7 \cdot \beta^3 + 7 \cdot \beta^4 + \beta^7 \approx 1.44 \cdot 10^{-4} \hspace{0.05cm}.\]
Aufgaben zum Kapitel
Aufgabe 1.14: Bhattacharyya–Schranke für BEC
Aufgabe 1.15: Distanzspektren von HC (7, 4, 3) und HC (8, 4, 4)
Aufgabe 1.16: Fehlerwahrscheinlichkeitsschranken für AWGN
Aufgabe 1.16Z: Schranken für die_Gaußsche Fehlerfunktion